宿迁学院学生考研结果影响分析

系统简介

2015级宿迁学院各专业学生的大学平时成绩与相关考研信息，利用方差分析法和Logistic回归分析法对数据进行分析。首先，通过单因素方差分析研究了性别、政治成绩、专业课成绩、数学成绩、英语成绩以及报考院校的性质对考研录取结果的影响，发现报考院校的性质不满足方差齐性，不适合做方差分析，而专业课成绩以及数学成绩对于考研的结果影响较为显著。其次，综合logistic向前回归模型和向后回归模型给出最终回归模型，定量地给出了政治成绩、数学成绩和专业课成绩对考研录取结果的影响，最后针对在校生有针对性地提出能够提高考研录取率的建议。
关键词 考研 影响因素 单因素方差分析 Logistic回归分析法

1方差分析基本理论

方差分析是一种较为常见的统计方法，可根据因素个数分为单、双因素方差分析。以下则是由这两种分析的步骤和观测结论。
1.1 单因素方差分析
1.1.1 基本假定
方差分析需要满足以下的三种假定[3]P108-12：
（1）假设在水平下的样本观测值来源于同一正态总体；
（2）假定所有正态总体（）都有相同的方差，也就是说具备方差齐性；
（3）各个数据相互独立。
1.1.2 方差分析步骤
（1）建立模型

（2）构造检验统计量
方差分析——通过使用组内方差和组间方差来构造检验统计量[3]P108-12，其中：
组间方差反映了由于水平的变化而导致的数据波动

组内方差反映了因随机误差的影响导致的数据波动

总平方和反映了所有数据的总波动大小

各项数据及来源皆见表1：
表1 单因素方差分析表
方差来源 平方和 自由度 均方和 F值 临界值 显著性
效应
误差
总和
其中：
.
（3）给定，确定拒绝域
拒绝域为

通常显著性水平分别取和
检验结果也可用表2表示：
表2方差分析临界值及显著性判断
条件 显著性
不显著
显著
显著
1.2 两因素方差分析
由两个因素对指标影响的独立与否，可将其分为以下…两类分析。
1.2.1 无交互作用的两因素方差分析
（1）建立模型

提出假设：

（2）构造检验统计量
总平方和 总自由度
A因素的组间方差平方和 A因素的自由度
B因素的组间方差平方和 B因素的自由度
组内方差平方和 误差自由度
检验统计量：
.

通常可用表3形式表示：
表3无交互作用的两因素方差分析表
方差来源 平方和 自由度 均方和 F值 临界值
因素A

因素B

误差
总和
（3）给定，确定拒绝域
拒绝域分别为；
.
1.2.2 有交互作用的两因素方差分析

（1）建立模型

提出假设

（2）构造检验统计量
总平方和与自由度

水平组合平方和与自由度

A因素组间方差平方和与自由度

B因素组间方差平方和与自由度

交互作用平方和与自由度

组内方差平方和与自由度

检验统计量：

列表如下：

表4有交互作用的方差分析表
方差来源 平方和 自由度 均方和 F值
因素A

因素B

交互作用

误差
总和

（4）给定，确定拒绝域
,
,
.

2 Logistic回归基本理论

2.1 Logistic概述
Logistics回归方程[7]89-93模型是并不是一种常用的统计方法，但接下来将对这种方法进行阐述并运用其进行数据分析。尽管其属于判别分析且效率在某些方面的运用不高，但由于它完善了线性回归模型的缺漏之处，同时可以避开分类型分量的分布问题，该方法在本研究分析中适用度较高。
2.2 Logistic分布
定义:设Z是连续随机变量，Z服从Logistic分布则表示Z具有下列分布函数和密度函数。

在上式中，为位置参数，为形状参数。其中满足Logistic分布的密度函数和分布函数的图像分别如下[3]P108-12：………………

图1 Logistic分布函数以及密度函数
特别地，当时，Logistic密度函数和分布函数分别如下：

通过Logistic的分布函数，可以发现，在中心点附近增长较快，而在两端增长较慢，根据这样的分布，可以很快将中心点附件的数据进行分类。

2.3 Logistic回归模型的数据结构
设资料中有一个因变量y、p个自变量，每个实验对象都共有n次观测结果，可将整理完成的原始资料表述如下表：
表5 Logistic回归模型数据结构
实验对象 …
1 …
2 …
3 …
… … … … … …
n …
其中：的取值为数值型或者分类型，y的取值是二值或多项分类。
2.4 Logistic回归模型
若发生的概率为p则它与自变量之间的Logistic回归模型为：

由上式可知，不发生的概率为：

通过数学变换得：

定义为Logistic变换，即

其中，之间是相互独立的，是影响因素增加一个单位所引起的对数优势的增量，其大小主要反映了其对Y的作用大小。
2.5 Logistic参数估计
在学习Logistic时，对于给定的数据集，其中，要想得到Logistic模型[8]P56-5，可以使用极大似然估计法来估计模型参数，再建立模型。
假设：，似然函数（联合概率分布函数）则为：

对数似然函数为：

一般在Logistic回归学习中，梯度下降法或者牛顿法都是较为常见的方法，也便以问题之间的转化，从逻辑回归问题变成以对数似然函数为目标函数的最优化问题。
2.6 Logistic回归模型小结
Logistic回归是概率模型，通常参数的估计值用极大似然估计法来计算，以下条件为此模型可用条件:
1、某事件的发生费率或是二分类的分类变量是因变量；
2、因变量及残差皆需服从二项分布，不是正态分布是由于二项分布对应的是分类变量，故需使用最大似然法进行解决而非是使用最小二乘法估计问题、检验问题；
3、Logistic的概率与自变量之间呈现线性关系；
4、每个观测对象之间相互独立。

3 宿迁学院学生考研结果影响因素的综合分析

3.1 数据收集及整理方法
对于学生考研结果的影响因素较多[9]P78-84，其中分为宏观因素以及微观因素。宏观上，国家的发展形势、经济发展状况、相关专业的就业背景等往往会对考研的形势结果产生一定的影响,这些都属于大趋势而非个人可以改变且对群体范围都有影响；微观因素上，主要包括文化水平、性别、报考学院以及复习程度的相关类别等，都是由于个体差别导致的不同和影响。在数据的收集上，我们主要考虑微观因素，即政治基础、数学能力、专业课基础，性别、报考学校性质等。在收集到的有效信息中，我们删除了缺失以及带有异常值的数据，共收集到有效信息1243条。
3.2 数据量化及构成
数据的收集主体主要为2015级考研学生，与考研有关的因素如下：……
性别：性别的区分往往会对学生个人的考研学习能力有一定的相关性。
政治基础：政治作为考研的必考科目之一，在考研成绩中占有重要的比例，因为其中主要包含了较多中国政治、历史及思想道德素质的知识体系，政治科目的成绩可以作为衡量考生考研基础的一大指标。
数学能力：针对考研的相关专业，数学能力往往体现一个人的逻辑分析能力，在考研成绩分布中，数学总分高达150分，数学成绩的高低往往影响考生考试排名的高低。
专业课基础：专业课的成绩往往体现了考生对专业基础框架的掌握程度，其贯穿了考研的初试和复试的始终，专业课掌握的程度越高，在复试环节往往会起到决定性因素，其在考试成绩中也占据了较高的比重，在专业课成绩的设置上，我们设置相关权重构成最终的专业成绩。
英语能力：英语在考研成绩分布中同样占据着重要的地位，根据已有的统计数据，有许多考生仅仅因为英语而考研惜败，同样，在考研复试中，英文翻译，英文交流同样能够对最终的考研结果构成一定的影响。
报考学校的性质：不同学校的考研难度具有一定的差异性，考生所报考的学校会对录取结果有一定的影响，因此将报考学校的性质纳入到考研结果的影响范围。在报考学校的划分上，设置报考211以上学校值设为1，普通高校为2。
为了较为清晰地展示本次数据的结构性，下表为各变量的统计属性。

由上表可知，在性别的差异上，男生考研成功率为25.7%，女生考研成功率为28.7%，两者并没有显著差异，而在相关基础成绩方面，无论是英语能力、数学能力、专业课基础或者政治基础，其对考研的录取率均存在一定的影响，至于报考学校的性质问题，普通高校的占据75%，而211以上院校的报考人数则占25%，其对应的成功率分别为24.4%以及6.4%，报考211以上院校的成功率明显低于报考普通院校的成功率。
3.3 单因素方差分析
在数据的选取上，考虑到不同的专业所考取的数学科目的不同，为了避免不同科目对考研结果的影响，我们选取了2015级考研科目最多的土木工程专业，它们专业考试科目与数学考试科目基本相同。
在相关的成绩设置中，政治成绩、英语成绩、数学成绩以及专业课成绩的算法皆为：

（1）性别对平时课程总分的影响，统计上述数据得，男生的平时课程成绩总分为315.79，而女生的平时课程成绩总分为339.27。其箱线图如下：

图2 性别箱线图
后续对性别进行方差齐性检验，其结果如下表：
表8性别方差齐性检验
Levene 统计量 df1 df2 显著性
0.89 1 73 .766
由上表可知，显著性0.766>0.005，所以具有方差齐性，因此针对男女性别数据进行进一步的单因素方差分析，结构见下表：
表9性别方差分析表
平方和 df 均方 F 显著性
组间 .003 1 .003 .022 .882
组内 10.077 73 .138
总数 10.080 74
从上表可以看出，p值为0.882>0.05，说明了性别的区分对考研录取结果的影响并不显著。
（2）英语成绩对考研录取结果的影响
将本次调查的考生录取结果分为，0为未录取，1为录取，我们针对2015级土木工程学院的学生近四年的与英语相关的课程成绩，统计到科目包括大学英语一、大学英语二、英语扩展课程一以及英语扩展课程二，根据其统计结果如下图所示：

图3 英语加权成绩箱线图
其中，考研录取的学生大学四年的平均英语加权成绩为76.56，而未录取的学生平均英语加权成绩为74.71，对英语成绩进行方差齐性检验,其结果如下表：
表11英语成绩方差齐性检验
Levene 统计量 df1 df2 显著性
.344 1 73 0.565
由表4可知，显著性0.565>0.05,具有方差齐性，进一步对有关录取情况的数据进行单因素方差分析，结果如下：
表12英语方差分析表
平方和 df 均方 F 显著性
组间 64.025 1 64.025 2.496 .118
组内 1872.870 73 25.656
总数 1936.895 74
根据上表，显著性值为0.118>0.005，说明了在考研录取结果中，大学四年英语课程的学习成绩对于考研结果的影响并不显著，影响不大。
（3）数学成绩对考研录取结果的影响
本次调查将录取情况分为录取以及未录取两种情况，统计到的数学成绩科目主要有：高数上、高数下、概率论、线性代数。通过调查，发现未录取的考生平均加权数学成绩在80.1406，而录取的考生平均加权数学成绩则在86.6458，其箱线图具体结果如下：

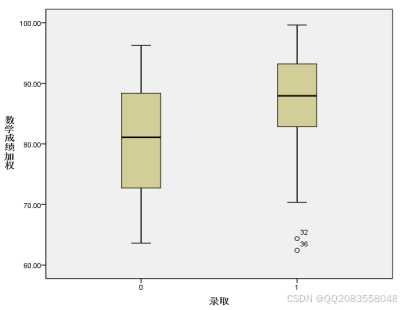
图4数学加权成绩箱线图
而其方差齐性检验结果如下表：
表13数学成绩方差齐性检验
Levene 统计量 df1 df2 显著性
.694 1 73 0.407
由显著性值可知，0.407>0.005数学成绩具有方差齐性，因此进一步对数据进行单因素方差分析，结果如下表所示：
表14数学成绩方差分析表
平方和 df 均方 F 显著性
组间 792.188 1 792.188 9.175 .003
组内 6302.873 73 86.341
总数 7095.061 74
由表中0.003<0.005可以看出大学四年的数学加权成绩对考研录取结果有着显著影响。
（4）专业课成绩对考研录取结果的影响
针对2015级土木工程学院考研学生，专业课成绩主要统计到以下几个科目：工程力学上、工程力学下、结构力学上以及结构力学下。根据数据统计，未录取的考生平均专业课加权成绩在77.3819，而录取的考生平均专业课加权成绩在83.859，其箱线图如下：

图5 专业课加权成绩箱线图
对其进行方差齐性检验，结果如下：
表15专业课成绩方差齐性检验
Levene 统计量 df1 df2 显著性
2.041 1 73 .157
由显著性p=0.157>0.005，可知，专业课成绩具有方差齐性，对其数据进行单因素方差分析，其结果具体见下表：
表16专业成绩方差分析表
平方和 df 均方 F 显著性
组间 785.340 1 785.340 9.423 .003
组内 6084.035 73 83.343
总数 6869.375 74
由显著性可知，专业课知识的掌握对考研录取结果同样有着重要的影响。
（5）政治成绩对考研录取结果的影响
针对政治成绩，由数据统计到的科目主要有：思修、马原、毛中特上以及毛中特下，未录取的加权政治成绩平均分为79.6944，而录取的加权政治平均分为79.5192，具体结果见下图：

图6 政治加权成绩箱线图

由显著性得出，在报考学院的性质上，发现显著性为0.000<0.005，表明方差齐性检验并未通过，也就是说不可以对其应用单因素方差分析。
3.4 Logistic回归分析
由以上描述及计算分析，我们发现有些因素对考研录取结果的影响不显著，而有些因素则较为显著，因此，在初始时，我们对所有的因素构建了Logistic回归模型。其初始回归模型数值如下表：

在初始回归模型中，根据显著性小于0.05的标准，我们发现只有政治成绩满足显著性，因此我们分别采用向前和向后回归法建立新的模型，在向前回归的方法中，先后剔除了性别、报考学校性质因素、数学成绩、英语成绩以及报考学院性质，而在向后回归的方法中，先后剔除了性别、报考学校性质、英语成绩三个因素，因此得到最终的解释模型分分别如下：

在向前和向后回归的模型中，两者的区别在于：向后主要将所有变量一次加入回归方程，按顺序剔除掉对回归方程影响并不显著的变量；而向前则是候选的变量逐个引入到回归方程，其是以不存在自变量的模型作为起点，然后逐步增加自变量并筛选自变量的过程。在最终回归模型的选择上，我们选择向后回归的模型，主要其方法侧重于全局最优性，而向前的方法则侧重于局部最优。
根据表23，可以得到最终的回归模型：
0.077+0.082
由上述回归模型，可以得到政治成绩、数学成绩和专业课成绩所对应的相关权重系数为-0.206，0.077，0.082。
由上式分析，在保持政治成绩与数学成绩不变的同时，专业课成绩每提高一分，其考研的成功率则增加8.55%；而保持政治成绩与专业成绩不变的同时，数学成绩每提高一份，其考研的成功率则提高8%，相较于政治成绩，专业课与数学的掌握程度比政治显得尤为重要。
3.5 Logistic回归模型评价
回归系数的解释依赖于回归模型的整体评价，因此，在完成模型构建之后，我们把每位考生解释变量的数据又重新带回到上述模型中，根据模型所计算出来的理论值与实际情况进行比较，进一步对模型进行评价。
表24 模型预测结果与考研结果对照表
学生录取结果 模型判定结果
未考上 考上
未考上 21 15
考上 7 32
根据上述表，模型判定正确的比重到近70.7%，其中对考研成功的判定正确的比重达到82.1%，对考研不成功的判定正确的比重达到58.3%，由此可见模型的整体预测效果较好。

结论

本文通过对各个学院的考研信息做了统计，针对土木工程学院2015级考研学生平时课程成绩，对其平时课程成绩利用加权的方法计算出其综合成绩并使用了Logistic回归分析、因素方差分析，对数据、问题等进行分析及阐述，得到如下结论：
（1）在性别上，男女考研比例相近且其录取成功率均为25.7 %以及28.7%，在单因素方差分析中，发现在满足方差齐性的情况下，其显著性大于0.005，性别的差异对于考研结果的影响并不显著。
（2）在单因素方差分析中，我们着重分析了性别、政治成绩、专业课成绩、数学成绩以及英语成绩，在满足方差齐性的前提下，发现只有专业课成绩以及数学成绩对于考研的结果影响较为显著，因此数学知识的掌握以及专业课基础的牢固程度往往对于考研的结果呈显著性影响。
（3）相较于男女性别，政治基础、数学能力、专业课基础以及英语能力这四个方面，我们的数据来源均统计于各个学院的考研学生的平时科目成绩，依靠科目类别划分以上四个方面，在构建的Logistic回归模型中，向前回归模型中政治成绩与专业课成绩其对应的系数分别为：-0.173、0.132；在向后回归模型中，政治课成绩、数学成绩、专业课成绩对应的系数分别为：-0.206、0.077、0.082，综合两种回归模型，发现其中专业课基础知识的掌握程度对于考研的录取结果影响较大，因此建议考研的学生在考研复习过程中，侧重于专业课以及数学的知识点的复习，这样对于考研成功率能有所提升。