poj2663

描述：

有一个3*n（0<=n<=30）的棋盘，用1*2的多米诺骨牌进行平铺。我们可以列举出很多种铺满的方法，本题要求我们计算铺满时的方法总数。例如：

3*2的棋盘，被1*2的多米诺骨牌平铺共有3种方法。

当n越大，越难用枚举法计算方法总数。

方法：

我们需要发现n不同时相互的规律。不难发现，当n为奇数时，平铺方法总数为0，因为不可能铺满棋盘。当n为偶数时，我们可以总结下面规律：

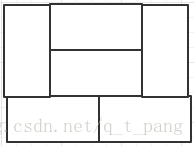
例如对上述棋盘，我们将棋盘分为左右两部分，右边部分是一个整体，不可拆散的。当右边部分为3*2时，

由上述可知，右边部分有3种可能，那么此时f(n)+=f(n-2)*3。当右边部分为3*4时，

右边是一个整体，并且不可拆散的做法只有两种

（灵魂画手。。。）和上图旋转180度的做法。所以f(n)+=f(n-4)*2。

当继续往下枚举时我们发现，当右边部分为4至m（m>=4且m为偶数）时，做法只有2种。至此，我们可以总结出规律为：

f(n)=f(n-2)*3+f(n-4)*2+f(n-6)*2+…+f(0)*2，注意f(0)=1

代码：

#include <iostream>
#include<string.h>
using namespace std;

int ans[35];

void dp(){
    ans[0]=1;
    ans[2]=3;
    for(int i=4;i<31;i+=2){
        ans[i]+=ans[i-2]*3;
        int j=4;
        while(j<=i){
            ans[i]+=ans[i-j]*2;
            j+=2;
        }
    }
}

int main()
{
    memset(ans,0,sizeof(ans));
    dp();
    int input;
    while(cin>>input){
       if(input==-1) break;
       cout<<ans[input]<<endl;
    }
    return 0;
}