这种题目怎么老是出现呀,好些题目都是整数拆分的题目。看了不弄懂是不行了,但是性质真的是太多了,学不完呀。今天先把这个这个关于整数拆分的题目全部简单类型弄懂吧:
第一种,就是存在顺序关系,问你N可以被拆分成几种:2^(n - 1),这是个排列组合的题目,不具有实际意义;
第二种,就是今天出现的这种题目,给你一个数,问你可以拆成多少种不同的方法?
这就比较麻烦了,但是人家研究出来了!我就佩服了。不过有喜欢研究了,慢慢研究研究就研究出来了,不过像咱们这种炮弹幌子,肯定是做不下来研究了。
是这样的。存在着这样的递归式子 P[N] = P[N - 1] + P[N - 2] - P[N - 3] - P[N - 5] + P[N - 7],其中N减去的数,是一种多边形数,叫做五边形数。广义的五边形数存在这样的公式 Five[x] = (3 * x * x - x) / 2;
那这样就好解出来了。但是今天貌似又出了一道这种划分的题目,我就泪奔了。一会看看题解;
另外,我挂上一位总结比较全面的博主的博文吧,大家共同学习:
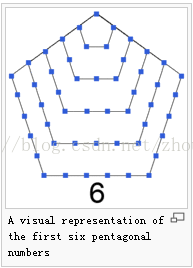
在将分拆数之前先介绍一点五边形数
http://en.wikipedia.org/wiki/Pentagonal_number
第n个五边形数公式:p(n)=(3*n^2-n)/2
前几个五边形数:1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001 .........
2. 广义五边形数:
n的取值0,1,-1,2,-2,3,-3.......
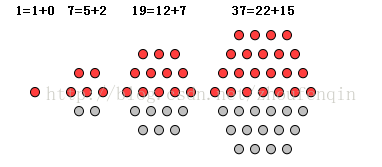
前几个广义五边形数:0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155, 176, 187, 210, 222, 247, 260, 287, 301, 330......
3. 中心五边形数:
4.中心六边形数
中心六边形数跟广义五边形数有较大的关系,见图
(相邻两个广义五边形数之和)
5. 五边形数测试
利用以下的公式可以测试一个正整数x是否是五边形数(此处不考虑广义五边形数):
若n是自然数,则x是五边形数,而且恰为第n个五边形数。
若n不是自然数,则x不是五边形数。
进入正题:分拆数
将一个数用一个或多个正整数的无序和来表示
例如4的分拆有5种:4 , 3+1 , 2+2 , 2+1+1 , 1+1+1+1
1. 限制分拆
给一些分拆加限制条件。例如8的分拆有22种,
其中分拆的数中全部都是奇数的有6种:7+1, 5+3, 5+1+1+1, 3+3+1+1, 3+1+1+1+1+1, 1+1+1+1+1+1+1+1;
同样,若要求8分拆的数中是两两不同的也有6种:8, 7+1, 6+2, 5+3, 5+2+1, 4+3+1
已证明一个数的分拆中满足以上两种条件的个数是相同的,详见http://en.wikipedia.org/wiki/Glaisher%27s_theorem
一些有关限制分拆的结论:
·n的分拆数中最大部分为m的个数=把n分拆成m部分的个数
如图,左边最大部分m=3,等于把n拆成3部分(右图) 把图转置即可
·n的分拆数中每一部分都小于等于m的个数=把n分成m份或更小
·n的分拆数中每部分的数都相等的个数=n 的因子个数
Eg. 6=2+2+2, 6=3+3,6=1+1+1+1+1+1
·n的分拆数中每部分都是1或2(或者把n分拆成1或2部分)的个数=floor(n/2+1);
Eg. 6=1+1+1+1+1+1, 6=1+1+1+1+2, 6=1+1+2+2, 6=2+2+2
·n的分拆数中每部分都是1或2或3(或者把n分拆成1或2或3部分)的个数=(n+3)^2/12;
2. 生成函数
因为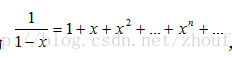
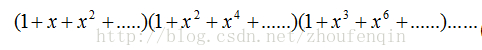
Pn 等于方程n=a1+2*a2+3*a3+...+n*an 的非负整数解a1,a2...an 的个数。
若是用母函数的方法去做,n很大不容易解出来,继续往下看
定义P(k,n)为:将n表示成>=k 的数之和。Eg P(3,6): 6=3+3
1) 当最小的数为k时,p(k,n) = p(k,n-k)。即在n-k表示成>=k的数之和的情况下再加入一个k,情况还是不变
2) 当最小的数>k时,则至少最小的数为k+1,p(k,n)=p(k+1,n);
所以p(k,n)=p(k,n-k)+p(k+1,n)。k>n 时,p(k,n)=0,p(n,n)=1;

得到下表:
| K n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
| 1 | 1 |
|
|
|
|
|
|
|
| 2 | 2 | 1 |
|
|
|
|
|
|
| 3 | 3 | 1 | 1 |
|
|
|
|
|
| 4 | 5 | 2 | 1 | 1 |
|
|
|
|
| 5 | 7 | 2 | 1 | 1 | 1 |
|
|
|
| 6 | 11 | 4 | 2 | 1 | 1 | 1 |
|
|
| 7 | 15 | 4 | 2 | 1 | 1 | 1 | 1 |
|
| ... |
|
|
|
|
|
|
|
|
前几个分拆数1, 1, 2, 3, 5, 7, 11, 15, 22, 30, 42 ,56,77,101,135......
如果是按p(k,n)=p(k+1,n)+p(k,n-k) 来算,复杂度仍是0(n^2),往下看
右边的分母是欧拉函数,可写成
可以发现等式右边x的指数为扩展五边形数,可根据之前介绍的扩展五边形公式算得p(n)=(3*n^2-n)/3,系数符号为(-1)^(m+1)
于是 p(k) = p(k − 1) + p(k − 2) − p(k − 5) − p(k − 7) + p(k − 12) + p(k − 15) − p(k − 22) − ...
Eg p(10)=p(9)+p(8)-p(5)-p(3)。复杂度降低了
贴出这个代码吧:
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
using namespace std;
const int MOD = 1000000007;
const int MAXN = 100000 + 11;
int N;
int P[MAXN];
long long Five(int x)
{
return ((long long)3 * x * x - x) / 2;
}
void init()
{
// memset(P, 0, sizeof(P));
P[0] = 1;
for (int i = 1; i < MAXN; i++)
{
int j = 1;
while (j)
{
long long k1 = Five(j);
long long k2 = Five(-j);
// cout << "k1 = " << k1 << endl;
// cout << "k2 = " << k2 << endl;
if (k1 <= i) //p[i - k1],p[i - k2]如果k1 k2都大于i了那怎么可能成立;
{
if (j & 1) // 如公式p[N] = p[N - 1] + p[N - 2] - p[N - 5] - p[N - 7];
{ //两个两个一个符号,并且奇数是正,偶数是负;
P[i] = ((long long)P[i] + P[i - k1]) % MOD;
}
else
{
P[i] = ((long long)P[i] - P[i - k1] + MOD) % MOD;
}
if (k2 > i)
{
break;
}
if (j & 1) // 如公式p[N] = p[N - 1] + p[N - 2] - p[N - 5] - p[N - 7];
{ //两个两个一个符号,并且奇数是正,偶数是负;
P[i] = ((long long)P[i] + P[i - k2]) % MOD;
}
else
{
P[i] = ((long long)P[i] - P[i - k2] + MOD) % MOD;
}
}
else
{
break;
}
j++;
}
// printf("P[%d] = %d\n", i, P[i]);
// system("pause");
}
}
int main()
{
int T;
init();
scanf("%d", &T);
while (T--)
{
scanf("%d", &N);
printf("%d\n", P[N]);
}
// system("pause");
return 0;
}
HDU-4658:
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <string>
using namespace std;
const int MAXN = 100000 + 11;
const int MOD = 1000000000 + 7;
long long q[MAXN];
long long p[MAXN];
long long getFive(int x)
{
return ((long long)x * x * 3 - x) / 2;
}
void init()
{
for (int i = 1; i < MAXN; i++)
{
if (i & 1)
{
q[i] = getFive(i / 2 + 1);
}
else
{
q[i] = getFive(i / 2 * -1);
}
// cout << q[i] << endl;
}
p[0] = 1;
for (int i = 1; i < MAXN; i++)
{
for (int j = 1; ; j++)
{
if (q[j] > i)
{
break;
}
else
{
int t = j;
if (t & 1)
{
t = t / 2 + 1;
}
else
{
t = t / 2;
}
if (t & 1)
{
p[i] = ((long long)p[i] + p[i - q[j]]) % MOD;
}
else
{
p[i] = ((long long)p[i] - p[i - q[j]] + MOD) % MOD;
}
}
}
// cout << p[i] << endl;
}
}
long long solve(int i, int k)
{
long long ans = 0;
for (int j = 0; ; j++)
{
if (q[j] * k > i)
{
break;
}
else
{
int t = j;
if (t & 1)
{
t = t / 2 + 1;
}
else
{
t = t / 2;
}
if (t & 1)
{
ans = ans - p[i - q[j] * k];
}
else
{
ans = ans + p[i - q[j] * k];
}
if (ans < 0)
{
ans = (ans + MOD) % MOD;
}
else
{
ans %= MOD;
}
}
}
return ans;
}
int main()
{
int N;
int K;
init();
int T;
scanf("%d", &T);
while (T--)
{
scanf("%d%d", &N, &K);
long long ans = solve(N, K);
printf("%lld\n", ans);
}
// system("pause");
return 0;
}








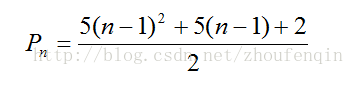
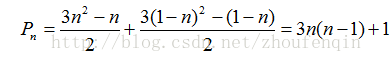
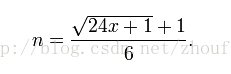
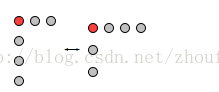
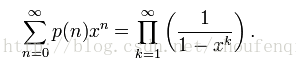















 5177
5177

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








