Fiduccia-Mattheyses algorithm概述

Fiduccia-Mattheyses algorithm

1.简介

以下是维基百科的原文简介：

FM algorithm is a linear time heuristic for improving network partitions. New features to  K-L heuristic :

• Aims at reducing net-cut costs; the concept of cutsize is extended to hypergraphs.
• Only a single vertex is moved across the cut in a single move.
• Vertices are weighted.
• Can handle "unbalanced" partitions; a balance factor is introduced.
• A special data structure is used to select vertices to be moved across the cut to improve running time.
• Time complexity O(P), where P is the total # of terminals

FM算法是一种改进网络分区的线性时间启发式算法，旨在减少不同分区之间的连接数，也就是分区之间的沟通成本，这种概念可以拓展到超图模型，

这个算法的主要目的是解决超图的双分区问题。

2.例子

以下通过一个例子来说明FM算法的基本原理：

在以下电路上执行FM算法

对电路进行超图建模：

1.初始化分区信息

其中右边的是超图表示，n是超边的集合，Set(n)={n1,n2,n3,n4......},n1包含了三个节点，{a,b,c}，如此类推。。

首先随机的将一个图进行分割，元件{a,c,d,g}在左边，元件{b,e,f,h}在右边

2.计算gain值和初始化

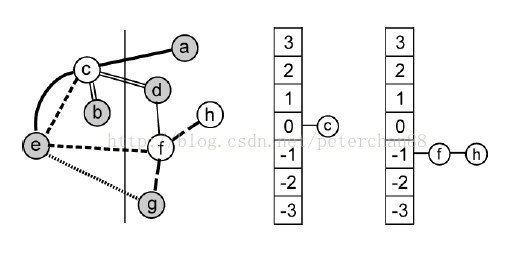
对于元件c，c包含在超边n1={a,c,e}，n3={c,f,e}，n2={b,c,d}中，其中在超边n3中，只有元件c在左边的集合中，其他的元件都在右边的集合中，因此FS(c)+1。

并没有超边中所有的元组都在左边，因此TE（c）=0。

FS（i），每当有超边包含了元件i，而且有且仅有i在元件i所属的分区（例如元组c在左边），FS（i）+1，FS（i）初始值为0。

TE（i），当有超边中所有元组都在元件i所属的分区（例如元组c在左边），TE（i）+1，TE（0）初始值为0

eg: FS(c) = 1,TE(c) = 0 ==》gain(c) = FS(c)+TE(c) = 1

计算出所有元件的gain值：

3.第一次移动

由上面第二步计算出所有元件的gain值，其中元件g和元件e的值都是2是最大的，而且对于g和e都是没有移动约束的。ps：移动约束的意思是尽量的使得两边的元件数量维持一致，不能有太大的偏差，左边的数量和右边的数量要尽量维持相等。这里根据字母的顺序，首先移动元件e。

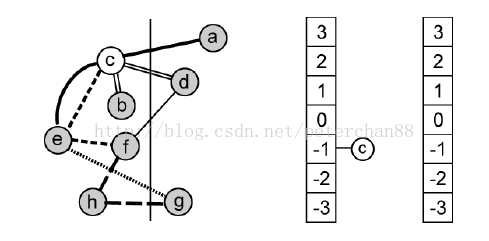
将e从右边移动到左边之后，将重新计算与e相关的元件的gain值。与e相关的元件集合{a,c,g,f}，重新计算gain（a） = FS（a）-TE（a） = 0-1 = -1，以此类推gain（c） = -1，gain（g） = 1-1 = 0，gain（f） = 2-0 = 2

4.第二次移动

虽然经过了第一次的移动gain（f）的值是最大的，但是f有区域的移动约束（要是移动了f，便导致了左边的元件数量远远大于右边的元件数量，所以f不能移动），选择d元件进行移动，随后计算被影响的元件{b,c,f}，gain（b） = 0-0 = 0，gain（c） = 1-1 = 0，gain（f） = 1-1 = 0

ps：已经移动过的元组就不用重新计算其gain值了，这样的做法使得算法收敛而且复杂性是线性的！

5.第三次移动

经过了两次的数据移动，g，c，h，f，b的gain值都是0，按照字母的顺利，选择b进行移动，老规矩！计算受影响的元件集合{c}，gain（c） = 0-1 = -1

6.第四次移动

g，h，f都是gain值的最大值，根据地域约束条件，选择g移动，计算受影响的元件{f，h}，gain（f） = 1-2 = -1，gain（h） = 0-1 = -1

7.第五次移动

按照字母顺序，选取a移动，计算受影响的元件集合{c}，gain（c） = 0-0 = 0

8第六次移动

根据地域约束，选择f元件进行移动，计算受影响的元件集合{h，c}，gain（h） = 0-0 = 0 gain（c） = 0-1 = -1 

9.第七次移动

我们移动h，没有受影响的元件集合。

10.第八次移动

移动c

11.中间数据

i代表的是每一步，cell就是每一步移动的元件cell，g（i）是每一步中的增益gain值，∑g（i）就是将每一步的增益值加起来，cutsize是两个分区之间的连接数，通俗点来说就是中间断开了多少条线。cutsize越少分区的质量越高。在这次的分割中得到了三个最优解分别是第二步，第三步，第四步，cutsize都是3，是最少的！

12.FM代码

github地址： https://github.com/peterchan1013/FM.git

https://github.com/peterchan1013/FM

关于编译：FM代码是C++代码，编译的时候使用C++11来编译，方法可以自行google，本人亲测在codeblock中可以运行

在codeblock中配置c++11，参考博客： http://blog.csdn.net/peterchan88/article/details/68955165