回归分析精要-CSDN博客

本文链接：https://blog.csdn.net/qingxiao__123456789/article/details/122542736

1.相关与回归

1.1 有监督的机器学习过程

        ●1.模式存在
        ●2.但无法用数学方式确定下来
        ●3.有数据可供学习

1.2 分类与回归

经过算法预测的结果是一个连续的值，我们称这样的问题为回归问题。

算法能够学会如何将数据分类到不同的类里，我们称这样的问题为分类问题。

回归问题:目标变量是连续值(数值预测) 分类问题:目标变量是离散值

1.3 回归的涵义

研究自变量与因变量之间的关系形式的分析方法。
目的:根据已知自变量来估计和预测因变量的值。

在回归分析中，把某一现象称为因变量，它是预测的对象，把引起这一现象变化的因素称为自变量，它是引起这一现象变化的原因。而因变量则反,映了自变量变化的结果。

1.4 案例分析

有20户家庭，冬天的取暖费用与3个因素有关:日间户外的平均温度，阁楼绝缘层的厚度，以及炉子的使用年数。如果某一家庭的平均户外温度是30F度，阁楼绝缘层的厚度为5英寸，炉子已使用过10年，它的冬天取暖费用为多少?

1.5 回归分析与相关分析

现实世界中,每一事物都与它周围的事物相互联系、相互影响，反映客观事物运动的各种变量之间也就存在着一定的关系。变量之间的关系可以分成两类:函数关系( 回归)和相关关系。

相关关系:反映事物之间的非严格、不确定的线性依存关系。
有两个显著的特点:
        ①事物之间在数量上确实存在一定的内在联系。表现在一个变量发生数量.上的变化，要影响另一个变量也相应地发生数量上的变化。例如：劳动生产率越高====>成本越低
        ②事物之间的数量依存关系不是确定的，具有一定的随机性。表现在给定自变量一个数值,因变量会有若干个数值和它对应，并且因变量总是遵循一定规律围绕这些数值平均数上下波动。其原因是影响因变量发生变化的因素不止一个。
        例:影响工业总产值的因素除了职工数外，还有固定资产原值、流动资金和能耗等因素。

1.6 相关分析

研究和测度两个或两个以上变量之间关系的方法有回归分析和相关分析。

相关分析:研究两个或两个以上随机变量之间线性依存关系的紧密程度。通常用相关系数表示，多元相关时用复相关系数表示。
回归分析:研究某一随机变量(因变量)与其他一个或几个普通变量(自变量)之间的数量变动的关系。更强调因果关系。

相关系数——对变量之间关系密切程度的度量：

        r的取值范围是[-1,1] :
                完全相关/完全正相关/完全负相关/不存在线性相关关系/负相关/正相关
                        ◆|r|>0.7为高度相关;
                        ◆|r| < 0.3为低度相关;
                        ◆0.3<| r| <0.7为中度相关。

相关系数的缺点: r接近于1的程度与n有关。当n较小时r的波动较大,当n较大时r的绝对值容易偏小。例如，n=2时，r的绝对值总为1 ( 两点连线总为一条直线)。

1.7 实战

例：有10个厂家的投入和产出如下，根据这些数据，我们可以认为投入和产出之间存在相关性吗?

程序实现：

import numpy as np
import pandas as pd
income=[20,40,20,30,10,10,20,20,20,30]
production=[30,60,40,60,30,40,40,50,30,70]
df=pd.DataFrame({'income':np.array(income),'production':np.array(production)})
print(df)
print(df.corr())#corr()函数，相关系数计算

结果：

income production
income 1.000000 0.759014
production 0.759014 1.000000

同样我们可以计算上述案例中取暖费的相关性分析，代码如下：

import numpy as np
import pandas as pd
A= [250,360, 165 , 43, 92, 200,355, 290 ,230, 120,73, 205 , 400,320,72,272, 94, 190, 235, 139]
B= [35, 29,36, 60, 65,30, 10,70,21,55, 54, 48,20,39, 60, 20, 58,40,27,30]
C= [3,4,7,6,5,5,6,10,9,2,12,5,5,4,8,5,7,8,9,7]
D= [6,10,3,9,6,5,7,10,11,5,4,1,15,7,6, 8,3,11,8,5]
df=pd.DataFrame({ '取暖费':np.array(A), '温度' :np.array(B), '厚度' :np.array(C), '年数': np.array(D)})
print(df)
print(df.corr())#计算全部的相关性分析
#u"我是含有中文字符组成的字符串。
print(df.corr()[u'温度'])#计算温度与其他属性的相关性
print(df[u'取暖费'].corr(df[u'温度']))#计算取暖费与温度的相关性

运行结果：

取暖费温度厚度年数
取暖费 1.000000 -0.661027 -0.257101 0.536728
温度 -0.661027 1.000000 0.178191 -0.315893
厚度 -0.257101 0.178191 1.000000 0.063617
年数 0.536728 -0.315893 0.063617 1.000000
取暖费 -0.661027
温度 1.000000
厚度 0.178191
年数 -0.315893
Name: 温度, dtype: float64
-0.6610265353019104

1.8 小结

2. 一元线性回归与最小二乘法

2.1 回归问题

根据自变量的多少(x的个数），回归模型可以分为一元回归模型和多元回归模型。
根据模型中自变量与因变量之间是否线性，可以分为线性回归模型和非线性回归模型。

应用回归分析预测需满足条件:
1.数据量不能太少(以多于20个较好) ;
2.预测对象与影响因素之间必须存在相关关系;

2.2 一元线性回归

一元线性回归 ( Linear regression)，只研究一个自变量与一个因变量之间的统计关系。对于只涉及一个自变量的简单线性回归模型可表示为:y= $\beta _{0}$ + $\beta _{1}$ x+ε

其中， $b_{0}$ 和 $b_{1}$ 称为模型的参数; ε是随机误差项，又称随机干扰项，有 ε~N(0,σ2)

2.3 最小二乘法

必首先需要确定选择这条直线的标准。这里介绍最小二乘回归法(least squaresregression )
必最小二乘回归法的基本思想:通过数学模型，拟合一条较为理想的直线，这条直线满足两点要求(1)原数列的观测值与模型估计值的离差平方和( 即所有点到该直线的垂直距离的平方和)为最小。(2) 原数列的观测值与模型估计值的离差总和为0。

离差： $e_{t}$ = $y_{t}$ - $\widehat{y_{t}}$ 离差和 : $\sum_{t=1}^{n}e_{t}=\sum_{t=1}^{n}(y_{t}-y\widetilde{}_{t})=0$ 离差平方和： $\sum_{t=1}^{n}e^{2}_{i}=\sum_{t=1}^{n}(y_{t}-y\widetilde{}_{t})^{2}$

最小二乘法的核心就是保证所有数据偏差的平方和最小(“ 平方”的在古时侯的称谓为“二乘”)。
        ●如果有一个变量，我们用直线拟合一些点，直线是y'=ax+b, 每点偏差是y-y',其中y是实际值，y'是估计值。
        ●sum( $(y-y')^{2}$ )最小时，直线拟合最好。
        ●试代入y'，可得M=sum( $(y-(ax+b))^{2}$ ), 对它求导取极值。
         ●此时，x,y是已知的，未知的是a和b,所以分别求M对a和b的偏导，解出的a,b即回归系数，记作W。
        ●线性回归就是计算参数W的过程。

高斯一马尔可夫定理
高斯马尔可夫定理( Gauss-Markov theory )在给定经典线性回归的假定下,最小二乘估计量是具有最小方差的线性无偏估计量。
高斯-马尔可夫定理的意义在于，当经典假定成立时,我们不需要再去寻找其它无偏估计量，没有一个会优于普通最小二乘估计量。也就是说，如果存在一个好的线性无偏估计量,这个估计量的方差最多与普通最小二乘估计量的方差- -样小，不会小于普通最小二乘估计量的方差。

举例理解定理：

假设手头有三个人的身高/体重调查数据:

又假设身高x和体重y关系的数学模型如下: y = ax + b

把调查数据代入.上面数学模型得到: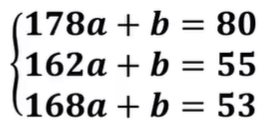

高斯当年是这样考虑的，方程可以写成如下形式:

实际_上可以合并成一-个式子: $(178a+b- 80)^{2}+ (162a+ b- 55)^{2}+(168a+b-53)^{2} =0$

虽然让.上式左边等于零很困难，但我们想办法让左边的值尽可能小，尽可能接近零。看看参数a,b取何值时，左边取得最小值。然后用这时a,b的值作为方程的近似解总可以吧?于是，求解方程组近似解的问题就变成求下面函数最小值问题了: $\varphi \left ( a,b \right )=(178a+b- 80)^{2}+ (162a+ b- 55)^{2}+(168a+b-53)^{2}$

其实还有很多可能的转化方法:

高斯提出无论使用哪种转换都不会比最下二乘法更好，所以我们普遍使用最小二乘法。

总结：

设简单线性回归模型y= $\beta _{0}$ + $\beta _{1}$ x+ε .中， $b_{0}$ 和 $b_{1}$ 是 $\beta _{0}$ 和 $\beta _{1}$ 的估计值。则y的估计值用 $\widehat{y}=b_{0}+b_{1}x$ 表示。我们要求出这样的待估参数bg和b1.使因变量的观察值与估计值之间的离差
平方和达到最小，即使极小。为此，分别求Q 对 $b_{0}$ 和 $b_{1}$ 的偏导，就可以求出符合要求的待估参数 $b_{0}$ 和 $b_{1}$ :

2.4 实战

数据如下图：

程序实现：

import numpy as np
from sklearn import linear_model
X= [522, 539 , 577, 613, 644, 670, 695,713, 741, 769, 801, 855, 842 , 860, 890, 920]
Y= [6700,7136, 7658,7784, 8108, 7583 , 8002, 8442, 8158, 8683, 9317 , 9675, 8542, 8584, 9612,9719]
x=np.array(X).reshape(-1,1)
y=np.array(Y).reshape(-1,1)
lr=linear_model.LinearRegression()
lr.fit(x,y)
print(lr.coef_)
print(lr.intercept_)
"""
reshape(行数，列数)常用来更改数据的行列数目

一般可用于numpy的array和ndarray, pandas的dataframe和series(series需要先用series.values把对象转化成ndarray结构)

那么问题来了reshape(-1,1)是什么意思呢？难道有-1行？
这里-1是指未设定行数，程序随机分配，所以这里-1表示任一正整数
所以reshape(-1,1)表示（任意行，1列）
"""

得到结果：（ $b_{0}$ 与 $b_{1}$ 的值）

[[6.52482712]]
[3605.13995199]

3. 多元线性回归与梯度下降法

3.1 简单例子

给定一套房屋的信息，如何预测其价格? ====> 预测价格= 0.8500 *面积+ 0.0500 *卧室数量

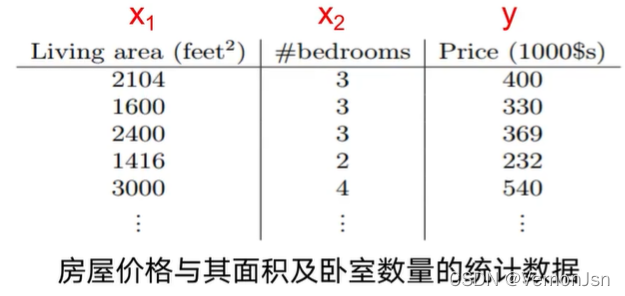
构建模型：，设 $x_{0}=1$ ;

这个方程称为回归方程，θ称为回归系数或权重

那么怎么得到 $\overrightarrow{\theta }$ 向量？

方向: $h\left ( \overrightarrow{x} \right )$ 要尽可能的接近y ; 为了衡量 $h\left ( \overrightarrow{x} \right )$ 有多“接近”y,定义损失函数( cost function )

$y^{(i)}$ 表示第i个训练实例对应的目标变量值，m为实例数量；常数1/2是为了方便计算; 此损失函数又叫最小二乘（least squares)损失函数。

并不是所有的函数都可以根据导数求出取得0值的点的，现实的情况可能是:
1.可以求出导数在每个点的值，但是直接解方程解不出来，
2.计算机更加适合用循环迭代的方法来求极值。

一个直观的思路是不断尝试，先假设一个初始参数值，计算损失函数值，再不断调整参数，并对比调整前后损失函数值的变化，如果函数值变小，则表示调整后的参数值比较好。这里就引出了梯度下降法。

3.2 梯度下降法

梯度下降法(Gradient descent)是-一个最优化算法，通常也称为最速下降法。1847年由著名的数学家柯西给出假设我们爬山，如果想最快上到山顶,那么我们应该从山势最陡的地方。上山。也就是山势变化最快的地方上山同样，如果从任意-一点出发,需要最快搜索到函数最大值，那么我们也应该从函数变化最快的方向搜索，函数变化最快的方向是函数的梯度方向.

如果函数为一元函数，梯度就是该函数的导数： $\triangledown$ f(x)= f '(x)
如果为二元函数，梯度定义为偏导数：

假设函数 $y=\left ( \theta _{1},\theta _{2},...,\theta _{n} \right )$ 只有一个极小点。
初始给定参数为 $\overrightarrow{\theta }=\left ( \theta _{1},\theta _{2},...,\theta _{n} \right )^{T}$ 。从这个点如何搜索才能找到原函数的极小值点?

方法:
1.首先设定一个较小的正数 $\alpha$ ，ε，以及迭代次数k;
2.求当前位置处的各个偏导数:

3.修改当前函数的参数值，公式如下:

其中 $\alpha$ 称为学习速率，即每次“前进”的步长

4.若参数变化量小于ε或已达迭代次数，退出;否则返回2

看个例子：利用梯度下降法求函数 $y=\frac{1}{2}\theta ^{2}-2\theta$ 的极小值

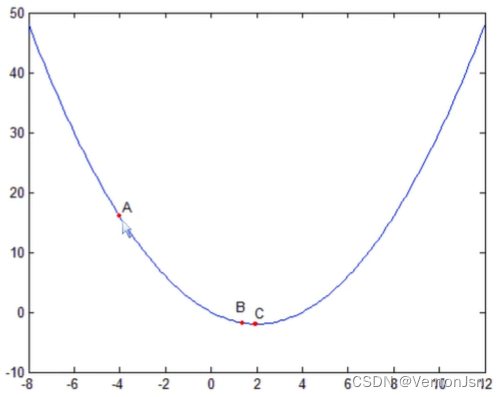
(1)设 $\alpha$ =0.9,ε=0.01,θ=-4
(2)计算导数: $\frac{dy }{d\theta}=\theta-2$

(3)计算当前导数值: y'=-6
(4)修改当前参数: 图中点B

(5)计算当前导数值: y'= -0.6
(6)修改当前参数: 图中点C

(7)计算当前导数值:y'=-0.06.
(8)修改当前参数:

(9)计算当前导数值:y'= -0.006
(10)修改当前参数:

(11)此时变化量满足终止条件，终止

简单起见，暂假设只有一一个训练样本，则

应用到不只一个训练样本的情况:

如果每次更新都计算整个训练集的数据样本
则成为批量梯度下降法( Batch Gradient Descent )

总结：

批量梯度下降算法每一步都要考虑整个数据集以计算梯度，这在数据集较大时计算成本很高
一种可选的方案是一次仅用一个样本(随机选取)来更新回归系数，该方法称为随机梯度下降算法(Stochastic gradient descent，SGD)

输入:a、迭代次数、初始化回归系数 $\overrightarrow{\theta }$

重复：

直到:达到迭代次数或收敛( 参数变化量已达到阀值)
其中其中a称为学习速率，即每次“前进”的步长

3.3 关于学习率

a过大容易“越过”极值点，导致不收敛，过小则收敛速度慢。
随着迭代次数的增加，-般要慢慢减小a(直观上，一开始前进快点，然后放慢速度)

3.4 实战

还是原先的例子：

import numpy as np
from sklearn import linear_model
A= [250,360, 165 , 43, 92, 200, 355 , 290 , 230,120, 73, 205 , 400 ,320,72,272, 94, 190,235,139]
B= [35, 29,36,60, 65,30,10, 70,21,55,54, 48,20,39, 60, 20,58,40,27 ,30]
C=[3,4,7,6,5,5, 6,10,9,2,12,5,5,4,8,5,7,8,9,7]
D=[6,10,3,9,6,5,7,10,11,5,4,1,15,7,6,8,3,11,8,5]
x=np. array([B,C,D]).T
y=np. array(A). reshape(-1,1)
lr=linear_model.LinearRegression()
lr.fit(x,y)
print(lr. coef_)
print (lr. intercept_)
test=np. array( [30,5, 10]). reshape(1, 3)
print('取暖费为: ' ,lr. predict(test))

实现效果：

[[-3.07146912 -8.21319349 12.35500321]]
[294.85253534]
取暖费为: [[285.19252626]]