算法学习--排序与查找

最新推荐文章于 2023-09-17 18:39:06 发布

qinzhaokun

最新推荐文章于 2023-09-17 18:39:06 发布

阅读量1.3k

点赞数

分类专栏： Algorithm

Algorithm 专栏收录该内容

31 篇文章 0 订阅

订阅专栏

二分查找

我们都知道二分查找算法，实际上二分查找以及其扩展应用是很广泛的。这里收集了一些和二分查找有关的有趣问题。强烈建议大家看完问题后最小化浏览器，先尝试自己去解决，然后再看代码，问题都不是太难。

问题1描述

给一个已经排序的数组，其中有N个互不相同的元素。要求使用最小的比较次数找出其中的一个元素。(你认为二分查找在排序数组里找一个元素是最优的算法的吗？)

不需要太多的理论，这是一个典型的二分查找算法。先看下面的代码：

int BinarySearch(int A[], int l, int r, int key)
{
    int m;
    while( l <= r )
    {
        m = l + (r-l)/2;
        if( A[m] == key ) //第一次比较
            return m;
        if( A[m] < key ) // 第二次比较
            l = m + 1;
        else
            r = m - 1;
    }
    return -1;
}

理论上，我们最多需要 logN+1 次比较。仔细观察，我们在每次迭代中使用两次比较，除了最后比较成功的一次。实际应用上，比较也是代价高昂的操作，往往不是简单的数据类型的比较。减少比较的次数也是优化的方向之一。

下面是一个比较次数更少的实现：

// 循环不变式： A[l] <= key &  A[r] > key
// 边界: |r - l| = 1
// 输入: A[l .... r-1]
int BinarySearch(int A[], int l, int r, int key)
{
    int m;
    while( r - l > 1 )
    {
        m = l + (r-l)/2;
        if( A[m] <= key )
            l = m;
        else
            r = m;
    }
    if( A[l] == key )
        return l;
    else
        return -1

在while循环中，我们仅依赖于一次比较。搜索空间( l->r )不断缩小，我们需要一个比较跟踪搜索状态。

需要注意的，要保证我们恒等式（A[l] <= key & A[r] > key）正确，后面还会用到循环不变式。

问题2描述

给一个有N个互不相同的元素的已排序数组，返回小于或等于给定key的最大元素。例如输入为 A = {-1, 2, 3, 5, 6, 8, 9, 10} key = 7,应该返回6.

分析：

我们可以用上面的优化方案，还是保持一个恒等式，然后移动左右两个指针。最终 left指针会指向小于或等于给定key的最大元素(根据恒等式A[l] <= key and A[r] > key)。

- > 如果数组中所有元素都小于key，左边的指针left 会一直移动到最后一个元素。

- > 如果数组中所有元素都大于key，这是一个错误条件，无答案。

- > 如果数组中的所有元素都 <= key，这是最坏的情况根据下面的实现

int Floor(int A[], int l, int r, int key)
{
    int m;
    while( r - l > 1 )
    {
        m = l + (r - l)/2;
        if( A[m] <= key )
            l = m;
        else
            r = m;
    }
    return A[l];
}
// 初始调用
int Floor(int A[], int size, int key)
{
    // 如果 key < A[0] 不符合条件
    if( key < A[0] )
        return -1;
    return Floor(A, 0, size, key);
}

问题3描述

给一个有重复元素的已排序数组，找出给定的元素key出现的次数，时间复杂度要求为logN.

分析

其实可以对上面的程序稍作修改，思路就是分别找出key 第一次出现的位置和最后一次出现的位置。

// 输入: 数组区间 [l ... r)
// 循环不变式: A[l] <= key and A[r] > key
int GetRightPosition(int A[], int l, int r, int key)
{
    int m;
    while( r - l > 1 )
    {
        m = l + (r - l)/2;
        if( A[m] <= key )
            l = m;
        else
            r = m;
    }
    return l;
}
// 输入: 数组区间 (l ... r]
// 恒等式: A[r] >= key and A[l] > key
int GetLeftPosition(int A[], int l, int r, int key)
{
    int m;
    while( r - l > 1 )
    {
        m = l + (r - l)/2;
        if( A[m] >= key )
            r = m;
        else
            l = m;
    }
    return r;
}
int CountOccurances(int A[], int size, int key)
{
    // 找出边界
    int left = GetLeftPosition(A, -1, size-1, key);
    int right = GetRightPosition(A, 0, size, key);
    // key有可能不存在，需要判断
    return (A[left] == key && key == A[right])?
           (right - left + 1) : 0;

问题4描述

有一个已排序的数组（无相同元素）在未知的位置进行了旋转操作，找出在新数组中的最小元素所在的位置。

例如：原数组 {1,2,3,4,5,6,7,8,9,10}，旋转后的数组可能是 {6,7,8,9,10, 1,2,3,4,5 }，也可能是 {8,9,10,1,2,3,4,5,6,7 }

分析：

我们不断的缩小 l 左指针和 r 右指针直到有一个元素。把上面划横线的作为第一部分，剩下的为第二部分。如果中间位置m落在第一部分，即A[m] < A[r] 不成立，我们排序掉区间 A[m+1 ... r]。如果中间位置m落在第二部分，即 A[m]<A[r]成立，我们缩小区间至 A[m+1 .... r ]。直到搜索的区间大小为1就结束。

int BinarySearchIndexOfMinimumRotatedArray(int A[], int l, int r)
{
    int m;
    // 先决条件: A[l] > A[r]
    if( A[l] <= A[r] )
        return l;
    while( l <= r )
    {
        //终止条件
        if( l == r )
            return l;
        m = l + (r-l)/2; // 'm' 可以落在第一部分或第二部分
        if( A[m] < A[r] )
            // (m < i <= r),可以排除 A[m+1 ... r]
            r = m;
        else
            // min肯定在区间 (m < i <= r),
            // 缩小区间至 A[m+1 ... r]
            l = m+1;
    }
    return -1;
}
int BinarySearchIndexOfMinimumRotatedArray(int A[], int size)
{
    return BinarySearchIndexOfMinimumRotatedArray(A, 0, size-1);
}

问题5描述

有一个已排序的数组（无相同元素）在未知的位置进行了旋转操作，找出在新数组中的指定元素所在的位置。

public class Solution {
    public int search(int[] nums, int target) {
        int l = 0;
        int r = nums.length-1;
        while(l < r){
            int mid = l + (r-l)/2;
            if(target == nums[mid]){
                return mid;
            }
            if(nums[l] < nums[r]){
                if(nums[mid] < target){
                    l = mid+1;
                }
                else{
                    r = mid-1;
                }
            }
            else{
                if(nums[mid] < nums[r]){
                    if(target > nums[mid] && target <= nums[r]){
                        l = mid+1;
                    }
                    else{
                        r = mid-1;
                    }
                }
                else{
                    if(target >= nums[l] && target < nums[mid]){
                        r = mid-1;
                    }
                    else{
                        l = mid+1;
                    }
                }
            }
        }
        if(nums[l] == target){
            return l;
        }
        else{
            return -1;
        }
    }
}

归并排序

归并排序是一个分治算法。归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个有序的子序列，再把有序的子序列合并为整体有序序列。 merg() 函数是用来合并两个已有序的数组. 是整个算法的关键。看下面的描述对mergeSort函数的描述：

MergeSort(arr[], l,  r)
If r > l
     //1. 找到中间点，讲arr分为两部分: 
             middle m = (l+r)/2
     //2. 对一部分调用mergeSort :  
             Call mergeSort(arr, l, m)
     //3.对第二部分调用mergeSort:
             Call mergeSort(arr, m+1, r)
     //4. 合并这两部分:
             Call merge(arr, l, m, r)

堆排序

堆排序是利用堆的性质进行的一种选择排序。下面先讨论一下堆。

1.堆

堆实际上是一棵完全二叉树，其任何一非叶节点满足性质：

Key[i]<=key[2i+1] && Key[i]<=key[2i+2]

或者

Key[i]>=Key[2i+1] && key>=key[2i+2]

即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。

堆分为大顶堆和小顶堆，满足Key[i]>=Key[2i+1] && key>=key[2i+2]称为大顶堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。

2.堆排序的思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

其基本思想为(大顶堆)：

1)将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；

2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];

3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

操作过程如下：

1)初始化堆：将R[1..n]构造为堆；

2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

下面举例说明：

给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

首先根据该数组元素构建一个完全二叉树，得到

Heroes Arrangement

然后需要构造初始堆，则从最后一个非叶节点 ( 程序中size/2)开始调整，调整过程如下：

20和16交换后导致16不满足堆的性质，因此需重新调整

这样就得到了初始堆。

即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

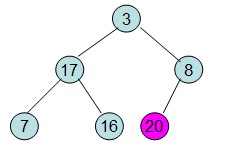此时3位于堆顶不满堆的性质，则需调整继续调整

这样整个区间便已经有序了。

从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。

void HeapAdjust(int *a,int i,int size)  //调整堆
{
    int lchild=2*i;       //i的左孩子节点序号
    int rchild=2*i+1;     //i的右孩子节点序号
    int max=i;            //临时变量
    if(i<=size/2)          //如果i是叶节点就不用进行调整
    {
        if(lchild<=size&&a[lchild]>a[max])
        {
            max=lchild;
        }   
        if(rchild<=size&&a[rchild]>a[max])
        {
            max=rchild;
        }
        if(max!=i)
        {
            swap(a[i],a[max]);
            HeapAdjust(a,max,size);    //避免调整之后以max为父节点的子树不是堆
        }
    }       
}
void BuildHeap(int *a,int size)    //建立堆
{
    int i;
    for(i=size/2;i>=1;i--)    //非叶节点最大序号值为size/2
    {
        HeapAdjust(a,i,size);   
    }   
}
void HeapSort(int *a,int size)    //堆排序
{
    int i;
    BuildHeap(a,size);
    for(i=size;i>=1;i--)
    {
        //cout<<a[1]<<" ";
        swap(a[1],a[i]);           //交换堆顶和最后一个元素，即每次将剩余元素中的最大者放到最后面
          //BuildHeap(a,i-1);        //将余下元素重新建立为大顶堆
          HeapAdjust(a,1,i-1);      //重新调整堆顶节点成为大顶堆
    }
}

归并排序对链表进行排序

归并排序通常是链表排序的第一选择。由于无法对链表随机访问，快速排序的的效果并不好，堆排序也是无法实现的。

为了和大部分数据结构中的链表结构保持一致，head表示链表的头节点，headRef表示指向头节点(head)的指针。注意，我们需要一个指针指向头节点MergeSort()中，因为以下实现将更改next，所以头节点必须改变如果原始数据头不是链表中的最小值

MergeSort(headRef)
//1) If head == NULL or 只有一个元素
    then return.
//2) Else 将链表分为两个部分 
      FrontBackSplit(head, &a, &b); /* a,b分别代表分割后的链表 */
//3) 分别对a,b排序
      MergeSort(a);
      MergeSort(b);
//4) 合并已排序的a,b ，并跟新 头指针headRef
     *headRef = SortedMerge(a, b);

计数排序-Counting Sort

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Θ(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

通俗地理解，例如有10个年龄不同的人，统计出有8个人的年龄比A小，那A的年龄就排在第9位,用这个方法可以得到其他每个人的位置,也就排好了序。当然，年龄有重复时需要特殊处理（保证稳定性），这就是为什么最后要反向填充目标数组，以及将每个数字的统计减去1的原因。算法的步骤如下：

找出待排序的数组中最大和最小的元素
统计数组中每个值为i的元素出现的次数，存入数组C的第i项
对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

假定输入是个数组A【1…n】， length【A】=n。另外还需要一个存放排序结果的数组B【1…n】，以及提供临时存储区的C【0…k】(k是所有元素中最大的一个)。算法伪代码：

下面看一个例子来理解：

假设数字范围在 0 到 9. 
输入数据: 1, 4, 1, 2, 7, 5, 2
  1) 使用一个数组记录每个数组出现的次数
  Index:     0  1  2  3  4  5  6  7  8  9
  Count:     0  2  2  0   1  1  0  1  0  0

  2) 累加所有计数（从C中的第一个元素开始，每一项和前一项相加）
  Index:     0  1  2  3  4  5  6  7  8  9
  Count:     0  2  4  4  5  6  6  7  7  7

更改过的计数数组就表示 每个元素在输出数组中的位置

  3) 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1
 例如对于: 1, 4, 1, 2, 7, 5, 2. 1 的位置是 2.
 把1放在输出数组的第2个位置.并把计数减 1，下一个1出现的时候就放在了第1个位置。(方向可以保持稳定)

public class CountingSort {
	// 类似bitmap排序
	public static void countSort(int[] a, int[] b, final int k) {
		// k>=n
		int[] c = new int[k + 1];
		for (int i = 0; i < k; i++) {
			c[i] = 0;
		}
		for (int i = 0; i < a.length; i++) {
			c[a[i]]++;
		}
		System.out.println("\n****************");
		System.out.println("计数排序第2步后,临时数组C变为：");
		for (int m : c) {
			System.out.print(m + " ");
		}

		for (int i = 1; i <= k; i++) {
			c[i] += c[i - 1];
		}
		System.out.println("\n计数排序第3步后,临时数组C变为：");
		for (int m : c) {
			System.out.print(m + " ");
		}

		for (int i = a.length - 1; i >= 0; i--) {
			b[c[a[i]] - 1] = a[i];// C[A[i]]-1 就代表小于等于元素A[i]的元素个数，就是A[i]在B的位置
			c[a[i]]--;
		}
		System.out.println("\n计数排序第4步后,临时数组C变为：");
		for (int n : c) {
			System.out.print(n + " ");
		}
		System.out.println("\n计数排序第4步后,数组B变为：");
		for (int t : b) {
			System.out.print(t + " ");
		}
		System.out.println();
		System.out.println("****************\n");
	}

	public static int getMaxNumber(int[] a) {
		int max = 0;
		for (int i = 0; i < a.length; i++) {
			if (max < a[i]) {
				max = a[i];
			}
		}
		return max;
	}

	public static void main(String[] args) {
		int[] a = new int[] { 2, 5, 3, 0, 2, 3, 0, 3 };
		int[] b = new int[a.length];
		System.out.println("计数排序前为：");
		for (int i = 0; i < a.length; i++) {
			System.out.print(a[i] + " ");
		}
		System.out.println();
		countSort(a, b, getMaxNumber(a));
		System.out.println("计数排序后为：");
		for (int i = 0; i < a.length; i++) {
			System.out.print(b[i] + " ");
		}
		System.out.println();
	}
}

线性时间内对范围在0-n^2内的数排序

这是一个面试题。问题描述：给一个大小为n的数组arr，每个元素都是范围在 0 到 n^2-1内的数字，如何在线性时间内对齐排序？

例子:
假设有5个元素,每个元素范围在 0 - 24.
Input: arr[] = {0, 23, 14, 12, 9}
Output: arr[] = {0, 9, 12, 14, 23}

假设有3个元素,每个元素范围在 0 - 8.
Input: arr[] = {7, 0, 2}
Output: arr[] = {0, 2, 7}

分析：基于比较的排序肯定是不能用了，最低复杂度为O(nlogn)，而题目要求为O(n)。复杂度为O(n) 的排序算法常见的有计数排序、基数排序和桶排序。

如果数据的范围都在0-n ，就可以直接用计数排序了，空间复杂度为O(n)。在考虑下基数排序，一般来说复杂度为 O(nk)，其中n是排序元素个数，k是数字位数，k的大小是取决于我们选取的底(基数)，一般对十进制数的话就选取的10. 这里为了把k变为常数，就可以取n为底，k就为2. 这样复杂度就为 O(n)了。即把这些数都看成是n进制的，位数则不会超过2

arr[] = {0, 10, 13, 12, 7}

假设以5为底(即5进制).  十进制的13 就为 23，十进制的 7为 12.
arr[] = {00(0), 20(10), 23(13), 22(12), 12(7)}

第一边遍历后 (根据最低位排序）
arr[] = {00(0), 20(10), 12(7), 22(12), 23(13)}

第二遍遍历后
arr[] = {00(0), 12(7), 20(10), 22(12), 23(13)}

其中，基数排序的实现，又要依赖稳定的计数排序，所以需要O(n)的空间来计数。就是两次计数排序。

代码实现如下：

#include<iostream>
using namespace std;

//对数组arr[]计数排序，根据 exp 指定的位
int countSort(int arr[], int n, int exp)
{
    int output[n]; // 结果数组
    int i, count[n] ;
    for (int i=0; i < n; i++)
       count[i] = 0;

    // count[]记录出现的次数
    for (i = 0; i < n; i++)
        count[ (arr[i]/exp)%n ]++;

    for (i = 1; i < n; i++)
        count[i] += count[i - 1];

    // 得到结果数组
    for (i = n - 1; i >= 0; i--)
    {
        output[count[ (arr[i]/exp)%n] - 1] = arr[i];
        count[(arr[i]/exp)%n]--;
    }

    // 再将排序结果复杂到 arr
    for (i = 0; i < n; i++)
        arr[i] = output[i];
}

// 使用基数排序
void sort(int arr[], int n)
{
    // 按最后一位排序，即 exp (n^0 = 1) 
    countSort(arr, n, 1);

    //按高位排序，即exp (n^1 = n )
    countSort(arr, n, n);
}

//打印数组
void printArr(int arr[], int n)
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
}

// 测试
int main()
{
    // 元素个数7, 范围在 0 - 48
    int arr[] = {40, 12, 45, 32, 33, 1, 22};
    int n = sizeof(arr)/sizeof(arr[0]);
    cout << "Given array is \n";
    printArr(arr, n);
    sort(arr, n);

    cout << "\nSorted array is \n";
    printArr(arr, n);
    return 0;
}

求第二小元素

一、题目

证明：在最坏情况下，利用n+ceil(lg n)-2次比较，即可得到n个元素中的第2小元素。（提示：同时找最小元素）。ceil表示向上取整

二、思考

step1：对所有元素，两个一组比较大小，小的一个进入下一轮比较。一直到比较出最小的元素。此时所有比较结果构成一棵二叉树。比较次数为n-1。

step2：沿着树从树根向下到叶子，找出第二小的元素，比较次数是ceil[lgn]-1。令m2[p]表示以p为根的树中的第二小元素。对于当前处理结点为p，key[p] = min{key[left[p]], key[right[p]]}。假设key[p] = key[left[p]]，则m2[p] = min{m2[left[p]], key[right[p]]}

可以这么理解：先找到最小的元素X，需要 n-1次比较。只有和X比较过的元素才有可能为第二小，和X比较过的元素个数为 ceil(lg n) 个，需要比较ceil(lg n)-1次，即上面蓝色圈中的数字。即总得比较次数为：n+ceil(lg n)-2

三、代码

#include <iostream>
using namespace std;
//第一遍求最小值的结果用树表示
struct node
{
	int key;
	node *next;//指向同一层中的下一个元素
	node *p;
	node *left;
	node *right;
	node(int k):key(k),next(NULL),p(NULL),left(NULL),right(NULL){}
};
//求第二小值
int Find_S2(node *head)
{
	node *p, *q, *r, *t;
	//step1：求最小值
	//两两比较，较小的一个进入下一轮，这个循环当只剩下一个元素时结束
	while(head->next != NULL)
	{
		//从第一个元素开始，head指向比完后较小的那一组数据中的第一个
		p = head;head = NULL;
		while(p)
		{
			//如果这组数据有奇数个，最后一个元素直接晋级
			if(p->next == NULL)
			{
				r = new node(p->key);
				r->left = p;
				p->p = r;
				p = p->next;
			}
			//p与p->next比较，较小的元素晋级
			else
			{
				q = p->next;
				r = new node(min(p->key, q->key));
				r->left = p;
				r->right = q;
				p->p = r;
				q->p = r;
				p = q->next;
			}
			//head指向比完后较小的那一组数据中的第一个，t用于把head指向的数据链成链表
			if(head == NULL)
			{
				head = r;
				t=  head;
			}
			else
			{
				t->next = r;
				t = r;
			}
		}
	}
	//step2：求最第二小值
	//Min用于存储最小值，Min2用于存储第二小值
	int Min = head->key, Min2 = 0x7fffffff;
	//从根结点向下比较
	p = head;
	//比较到叶子结点时循环结束
	while(p->left != NULL)
	{
		//当前结点的值来源于右孩子
		if(p->right && p->right->key == Min)
		{
			Min2 = min(Min2, p->left->key);
			p = p->right;
		}
		//当前结点的值来源于左孩子
		else
		{
			//由左孩子直接晋级的情况
			if(p->right)
				Min2 = min(Min2, p->right->key);
			p = p->left;
		}
	}
	return Min2;
}
//测试
int main()
{
	int A[8] = {0};
	node *head = NULL;
	//生成8个随机测试数据
	for(int i = 0; i < 8;i++)
	{
		A[i] = rand() % 100;
		//构造成树的最底层结点
		node *p = new node(A[i]);
		p->next = head;
		head = p;
	}
	//运行算法并输出结果
	cout<<Find_S2(head)<<endl;
	return 0;
}

问题4描述

有一个已排序的数组（无相同元素）在未知的位置进行了旋转操作，找出在新数组中的最小元素所在的位置。

qinzhaokun

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
算法学习--排序与查找

二分查找我们都知道二分查找算法，实际上二分查找以及其扩展应用是很广泛的。这里收集了一些和二分查找有关的有趣问题。强烈建议大家看完问题后最小化浏览器，先尝试自己去解决，然后再看代码，问题都不是太难。问题1描述给一个已经排序的数组，其中有N个互不相同的元素。要求使用最小的比较次数找出其中的一个元素。(你认为二分查找在排序数组里找一个元素是最优的算法的吗？)不需要太多的理
复制链接

扫一扫