最大流问题-Ford-Fulkerson算法
问题:
有一个自来水管道运输系统,起点是s,终点是t,途中经过的管道都有一个最大的容量。求从s到t的最大水流量是多少?
网络最大流问题是网络的另一个基本问题。许多系统包含了流量问题。例如交通系统有车流量,金融系统有现金流,控制系统有信息流等。许多流问题主要是确定这类系统网络所能承受的最大流量以及如何达到这个最大流量。
如下图所示:
最大的流量是 23:
比较常见的是Ford-Fulkerson解法。该方法依赖于三种重要思想:残留网络,增广路径和割。
在介绍着三种概念之前,我们先简单介绍下Ford-Fulkerson方法的基本思想。首先需要了解的是Ford-Fulkerson是一种迭代的方法。开始时,对所有的u,v属于V,f(u,v)=0(这里f(u,v)代表u到v的边当前流量),即初始状态时流的值为0。在每次迭代中,可以通过寻找一个“增广路径”来增加流值。增广路径可以看做是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。反复进行这一过程,直到增广路径都被找出为止。
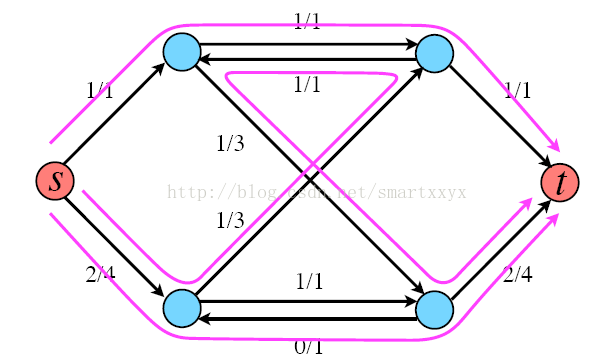
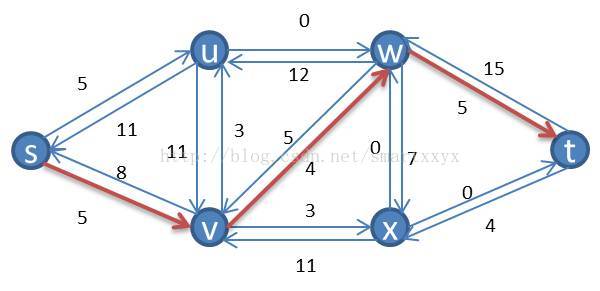
举个例子来说明下,如图所示,每条红线就代表了一条增广路径,当前s到t的流量为3。
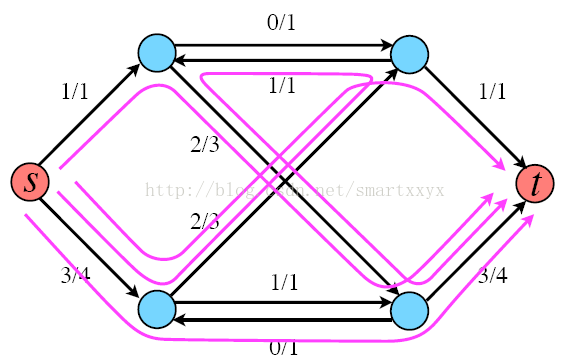
当然这并不是该网络的最大流,根据寻找增广路径的算法我们其实还可以继续寻找增广路径,最终的最大流网络如下图所示,最大流为4。
接下来我们就介绍如何寻找增广路径。在介绍增广路径之前,我们首先需要介绍残留网络的概念。
一、残留网络
顾名思义,残留网络是指给定网络和一个流,其对应还可以容纳的流组成的网络。具体说来,就是假定一个网络G=(V,E),其源点s,汇点t。设f为G中的一个流,对应顶点u到顶点v的流。在不超过C(u,v)的条件下(C代表边容量),从u到v之间可以压入的额外网络流量,就是边(u,v)的残余容量(residual capacity),定义如下:
r(u,v)=c(u,v)-f(u,v)
举个例子,假设(u,v)当前流量为3/4,那么就是说c(u,v)=4,f(u,v)=3,那么r(u,v)=1。
我们知道,在网络流中还有这么一条规律。从u到v已经有了3个单位流量,那么从反方向上看,也就是从v到u就有了3个单位的残留网络,这时r(v,u)=3。可以这样理解,从u到v有3个单位流量,那么从v到u就有了将这3个单位流量的压回去的能力。
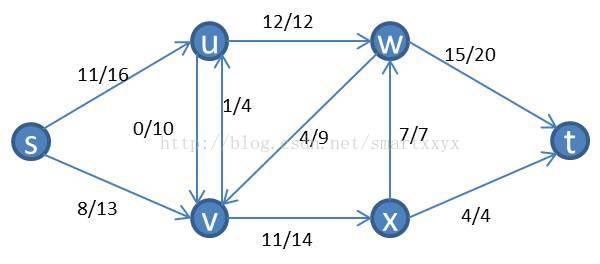
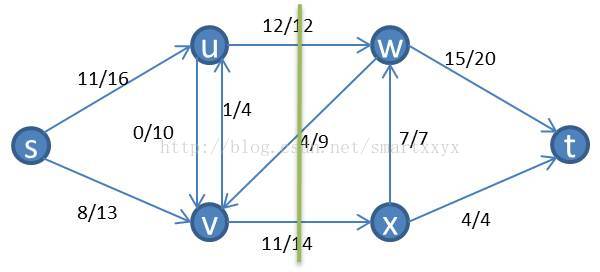
我们来具体看一个例子,如下图所示一个流网络
其对应的残留网络为:
二、增广路径
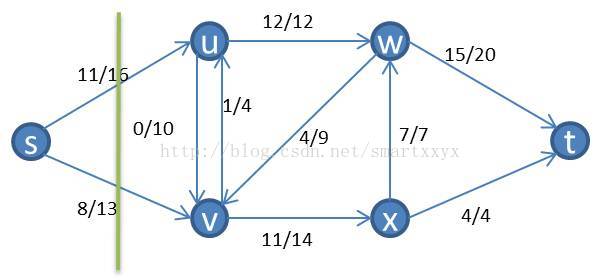
在了解了残留网络后,我们来介绍增广路径。已知一个流网络G和流f,增广路径p是其残留网络Gf中从s到t的一条简单路径。形象的理解为从s到t存在一条不违反边容量的路径,向这条路径压入流量,可以增加整个网络的流值。上面的残留网络中,存在这样一条增广路径:
其可以压入4个单位的流量,压入后,我们得到一个新的流网络,其流量比原来的流网络要多4。这时我们继续在新的流网络上用同样的方法寻找增广路径,直到找不到为止。这时我们就得到了一个最大的网络流。
三、流网络的割
上面仅仅是介绍了方法,可是怎么证明当无法再寻找到增广路径时,就证明当前网络是最大流网络呢?这就需要用到最大流最小割定理。
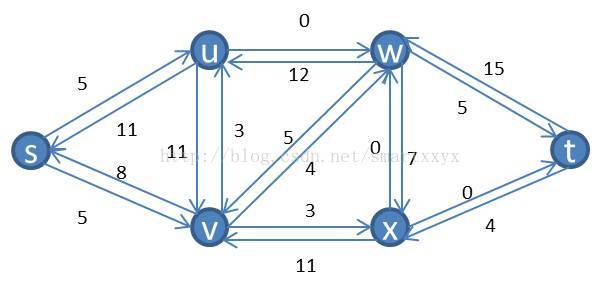
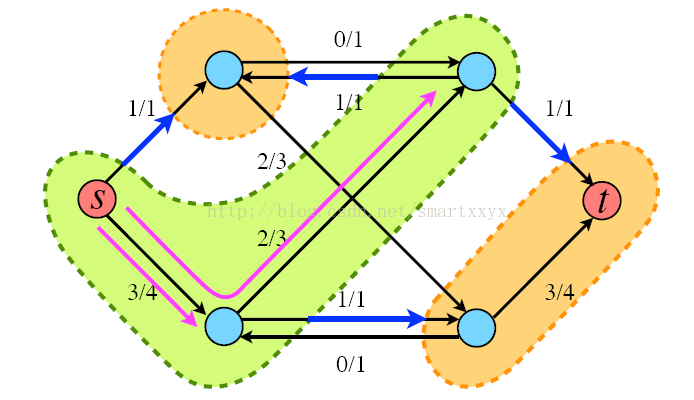
首先介绍下,割的概念。流网络G(V,E)的割(S,T)将V划分为S和T=V-S两部分,使得s属于S,t属于T。割(S,T)的容量是指从集合S到集合T的所有边(有方向)的容量之和(不算反方向的,必须是S-àT)。如果f是一个流,则穿过割(S,T)的净流量被定义为f(S,T)(包括反向的,SàT的为正值,T—>S的负值)。将上面举的例子继续拿来,随便画一个割,如下图所示:
割的容量就是c(u,w)+c(v,x)=26
当前流网络的穿过割的净流量为f(u,w)+f(v,x)-f(w,v)=12+11-4=19
显然,我们有对任意一个割,穿过该割的净流量上界就是该割的容量,即不可能超过割的容量。所以网络的最大流必然无法超过网络的最小割。
可是,这跟残留网络上的增广路径有什么关系呢?
首先,我们必须了解一个特性,根据上一篇文章中讲到的最大流问题的线性规划表示时,提到,流网络的流量守恒的原则,根据这个原则我们可以知道,对网络的任意割,其净流量的都是相等的。具体证明是不难的,可以通过下图形象的理解下,
和上面的割相比,集合S中少了u和v,从源点s到集合T的净流量都流向了u和v,而在上一个割图中,集合S到集合T的流量是等于u和v到集合T的净流量的。其中w也有流流向了u和v,而这部分流无法流向源点s,因为没有路径,所以最后这部分流量加上s到u和v的流量,在u和v之间无论如何互相传递流,最终都要流向集合T,所以这个流量值是等于s流向u和v的值的。将s比喻成一个水龙头,u和v流向别处的水流,都是来自s的,其自身不可能创造水流。所以任意割的净流量都是相等的。
万事俱备,现在来证明当残留网络Gf中不包含增广路径时,f是G的最大流。
假设Gf中不包含增广路径,即Gf不包含从s到v的路径,定义S={v:Gf中从s到v存在一条通路},也就是Gf中s能够有通路到达的点的集合,显然这个集合不包括t,因为s到t没有通路。这时,我们令T=V-S。那么(S,T)就是一个割。如下图所示:
那么,对于顶点u属于S,v属于T,有f(u,v)=c(u,v)。否则(u,v)就存在残余流量,因而s到u加上u到v就构成了一条s到v的通路,所以v就必须属于S,矛盾。因此这时就表明当前流f是等于当前的割的容量的,因此f就是最大流。
该算法可以简单的描述如下:
1) 初始化flow为0
2)While (存在从s到t的增广路径,设其流量为path-flow)
flow += path-flow;
更新残留网络;
3) return flow
import java.util.LinkedList;
import java.util.Queue;
public class MinFlow {
public static int V = 6;
/**
*
* @param rGraph 残留网络
* @param s 源点
* @param t 终点
* @param path 路径
* @return 是否可以在rGraph中找到一条从 s 到 t 的路径
*/
public static boolean hasPath(int rGraph[][], int s, int t, int path[]) {
boolean visited[] = new boolean[V];
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
//标准的BFS算法
while(queue.size() > 0){
int top = queue.poll();
for(int i=0; i<V; i++){
if(!visited[i] && rGraph[top][i] > 0){
queue.add(i);
visited[i] = true;
path[i] = top;
}
}
}
return visited[t] == true;
}
/**
*
* @param graph 有向图的矩阵表示
* @param s 源点
* @param t 终点
* @return 最大流量
*/
private static int maxFlow(int[][] graph,int s, int t) {
int rGraph[][] = new int[V][V];
for(int i=0; i<V; i++)
for(int j=0; j<V; j++)
rGraph[i][j] = graph[i][j];
int maxFlow = 0;
int path[] = new int[V];
while(hasPath(rGraph, s, t, path)){
int min_flow = Integer.MAX_VALUE;
//更新路径中的每条边,找到最小的流量
for(int v=t; v != s; v=path[v]){
int u = path[v];
min_flow = Math.min(min_flow, rGraph[u][v]);
}
//更新路径中的每条边
for(int v=t; v != s; v=path[v]){
int u = path[v];
rGraph[u][v] -= min_flow;
rGraph[v][u] += min_flow;
}
maxFlow += min_flow;
}
return maxFlow;
}
public static void main(String[] args) {
//创建例子中的有向图
int graph[][] = { { 0, 16, 13, 0, 0, 0 },
{ 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 },
{ 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 },
{ 0, 0, 0, 0, 0, 0 } };
V = graph.length;
int flow = maxFlow(graph, 0, 5);
System.out.println("The maximum possible flow is :" + flow);
}
}判断强连通图
问题:
给一个有向图,判断给图是否是强连通的。
如下图所示,则是一个强连通图:
对于无向图则比较简单,只需要从某一个顶点出发,使用BFS或DFS搜索,如果可以遍历到所有的顶点,则给定的图是连通的。
但这种方法对有向图并不使用,例如 : 1 -> 2 -> 3 -> 4,并不是强连通图。
方法一
可以调用DFS搜索 V 次,V是顶点的个数,就是对每个顶点都做一次DFS搜索,判断是否可达。这样的复杂度为O(V*(V+E))
方法二
可以参考求解连通分量的算法,我们可以在O(V+E) 的时间内找到所有的连通分量,如果连通分量的个数为1,则说明该图是强连通的。
Kosaraju 算法即为算法导论一书给出的算法,比较直观和易懂。这个算法可以说是最容易理解,最通用的算法,其比较关键的部分是同时应用了原图G和反图GT。 它利用了有向图的这样一个性质,一个图和他的transpose graph(边全部反向)具有相同的强连通分量!
#include <iostream>
#include <list>
#include <stack>
using namespace std;
class Graph
{
int V; // 顶点个数
list<int> *adj; // 邻接表存储
// DFS遍历,打印以v为起点的 强连通分量
void DFSUtil(int v, bool visited[]);
public:
Graph(int V) { this->V = V; adj = new list<int>[V];}
~Graph() { delete [] adj; }
void addEdge(int v, int w);
//判断是是否是强连通图
bool isSC();
// 得到当前图的逆置
Graph getTranspose();
};
void Graph::DFSUtil(int v, bool visited[])
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
DFSUtil(*i, visited);
}
// 返回当前图的转置图
Graph Graph::getTranspose()
{
Graph g(V);
for (int v = 0; v < V; v++)
{
list<int>::iterator i;
for(i = adj[v].begin(); i != adj[v].end(); ++i)
{
g.adj[*i].push_back(v);
}
}
return g;
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
}
bool Graph::isSC()
{
bool visited[V];
for (int i = 0; i < V; i++)
visited[i] = false;
DFSUtil(0, visited);
//如果有没有被访问的点就返回false
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
// 创建当前图的转置图
Graph gr = getTranspose();
for(int i = 0; i < V; i++)
visited[i] = false;
gr.DFSUtil(0, visited);
// 查看是否是所有的点都被访问到
for (int i = 0; i < V; i++)
if (visited[i] == false)
return false;
return true;
}
// 测试
int main()
{
// 创建图1
Graph g1(5);
g1.addEdge(0, 1);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.addEdge(3, 0);
g1.addEdge(2, 4);
g1.addEdge(4, 2);
g1.isSC()? cout << "Yes\n" : cout << "No\n";
// 创建图2
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.isSC()? cout << "Yes\n" : cout << "No\n";
return 0;
}二分图判断-Problem A.Bad Horse
题目来自 Google codejam :Practice Round China New Grad Test 2014 Problem A. Bad Horse
此题其实就是一个判断一个图是否是二分图。
二分图的定义
设G=(V,E)是一个无向图。如顶点集V可分割为两个互不相交的子集,并且图中每条边依附的两个顶点都分属两个不同的子集。则称图G为二分图。也就是说在二分图中,顶点可以分为两个集合X和Y,每一条边的两个顶点都分别位于X和Y集合中。如下图所示:
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。可以将 和
和  当做 着色图:
当做 着色图: 中所有节点为蓝色,
中所有节点为蓝色, 中所有节点着绿色,每条边的两个端点的颜色不同,符合图着色问题的要求。相反,用这样的着色方式对非二分图是行不通的,根据triangle:其中一个顶点着蓝色并且另一个着绿色后,三角形的第三个顶点与上述具有两个颜色的顶点相连,无法再对其着蓝色或绿色。
中所有节点着绿色,每条边的两个端点的颜色不同,符合图着色问题的要求。相反,用这样的着色方式对非二分图是行不通的,根据triangle:其中一个顶点着蓝色并且另一个着绿色后,三角形的第三个顶点与上述具有两个颜色的顶点相连,无法再对其着蓝色或绿色。
例如对于下面的图,可以用两种颜色进行着色。
下面的图则不可以:
可以使用回溯法解决图的M着色问题,但是对个这个特殊的问题,可以使用 BFS解决。算法过程为:借助队列,进行宽度优先遍历,先对一个起点着色RED,然后将其所有相邻的节点着色为BLUE,并加入队列。只要能保证相邻的节点是不同的颜色即可。
下面的Java代码是针对 Bad Horse 的题解,大家可以只关注isBipartite函数
public class BasHorse {
static int n;
static int T, index, cnt;
static int map[][];
public static void main(String[] args) {
try {
String path = "D:\\CPP\\code-jam\\A-small-practice-2.in";
Scanner scan = new Scanner(new File(path));
String outputPath = path.replace(".in", "out.txt");
File file = new File(outputPath);
FileOutputStream fos = new FileOutputStream(file);
T = scan.nextInt();
Map<String,Integer> mapSet = new HashMap<String,Integer>();
for(int i=0; i<T; i++){
mapSet.clear();
n = scan.nextInt();
index = 0;
map = new int[n*2][n*2];//最多会有2n个
for(int j =0; j<n; j++){
String str1 = scan.next();
Integer a ;
if( (a = mapSet.get(str1)) == null){
a = index;
mapSet.put(str1, index);
index++;
}
String str2 = scan.next();
Integer b ;
if( (b = mapSet.get(str2)) == null){
b = index;
mapSet.put(str2, index);
index++;
}
map[a][b] = 1;
map[b][a] = 1;
}
boolean isbit = isBipartite(map,index);
String output = "Case #" + (i+1) + ": ";
if(isbit) output += "Yes\r\n";
else output += "No\r\n";
try {
fos.write(output.getBytes());
} catch (IOException e) {
e.printStackTrace();
}
System.out.println(isbit);
}
} catch (FileNotFoundException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
}
private static boolean isBipartite(int[][] map,int n) {
//colorArr[i] 代表第i个结点的颜色
int colorArr[] = new int[n];
colorArr[0] = 1;
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(0);
while(!queue.isEmpty()){
int top = queue.poll();
for(int i=0; i<n; i++){
if(map[top][i] == 1 && colorArr[i] == 0){
colorArr[i] = 3 - colorArr[top];//两种颜色 1和2 交替着色
queue.add(i);
}else if(map[top][i] == 1 && colorArr[i] == colorArr[top] ){
return false;
}
}
}
return true;
}
}有向无环图的最短路径
问题
给定一个有向无环图和一个源点,求从该源点到其他所有的顶点的最短路径。我们已经知道了如何通过Dijkstra算法在非负权图中找到最短路径。即使图中有负权边,我们也知道通过Bellman-Ford算法找到一个从给定的源点到其它所有节点的最短路径。现在我们将看到一个在线性时间内运行得更快的算法,它可以在有向无环图中找到从一个给定的源点到其它所有可达顶点的最短路径。基本思想是利用拓扑排序。
分析
关于有向无环图(DAG)我们首先要知道,它们可以很容易地进行拓扑排序。拓扑排序应用范围非常之广,其中最常用的或许就是用于安排依赖任务(依赖任务是同属于一个工作中相同任务的实体,这些实体是保证互连的,它们解决共同的问题)。
下图即为对一个有向图的拓扑排序:
拓扑排序通常是用来“排序”依赖任务的!
经过拓扑排序,我们最终会得到一张DAG图的顶点列表,我们确信在拓扑排序列表中如果存在一条边(u,v),那么顶点u会先于顶点v进入列表中。
如果有一条边(u,v),那么顶点u一定在顶点v前面。这个结果通过这张图片变得更加通俗易懂。其中B和D之间没有边,但在列表中B在D前面!
此信息异常重要,我们唯一需要做的事情就是通过这个排序列表来计算距离最短的路径,这和Dijkstra算法比较相似。
好了,让我们来总结一下这个算法:
-首先,我们必须对有向无环图进行拓扑排序;
-其次,我们将到源点的距离初始化为0并将到其它所有顶点的距离设置为无穷大;
-最后,对于列表中的每一个顶点,我们从它的所有邻节点中找到最短路径的那个顶点;
这很像Dijkstra算法,但是其主要区别是我们使用的是经过拓扑排序的列表。
以下的图从这里的英文讲义拿来的:http://www.utdallas.edu/~sizheng/CS4349.d/l-notes.d/L17.pdf。演示了逐步找到最短路径的过程:
伪代码描述如下:
1) Initialize dist[] = {INF, INF, ….} and dist[s] = 0 where s is the source vertex.
2) Create a toplogical order of all vertices.
3) Do following for every vertex u in topological order.
………..Do following for every adjacent vertex v of u
………………if (dist[v] > dist[u] + weight(u, v))
………………………dist[v] = dist[u] + weight(u, v)
C++代码实现如下:
#include<iostream>
#include <list>
#include <stack>
#include <limits.h>
#define INF INT_MAX
using namespace std;
// 邻接表节点
class AdjListNode
{
int v;
int weight;
public:
AdjListNode(int _v, int _w) { v = _v; weight = _w;}
int getV() { return v; }
int getWeight() { return weight; }
};
// 图
class Graph
{
int V; // 顶点个数
list<AdjListNode> *adj;
void topologicalSortRecall(int v, bool visited[], stack<int> &stk);
public:
Graph(int V);
void addEdge(int u, int v, int weight);
void shortestPath(int s);
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<AdjListNode>[V];
}
void Graph::addEdge(int u, int v, int weight)
{
AdjListNode node(v, weight);
adj[u].push_back(node);
}
// 拓扑排序,递归调用。详细解释参考这里:
void Graph::topologicalSortRecall(int v, bool visited[], stack<int> &stk)
{
// 标记当前节点是访问过的
visited[v] = true;
list<AdjListNode>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
AdjListNode node = *i;
if (!visited[node.getV()])
topologicalSortRecall(node.getV(), visited, stk);
}
stk.push(v);
}
// 从给定的源点s 找出到其它顶点的最短距离.
void Graph::shortestPath(int s)
{
stack<int> stk;
int dist[V];
//标记所有顶点为未访问过的
bool *visited = new bool[V];
for (int i = 0; i < V; i++)
visited[i] = false;
// 拓扑排序,结果存入stk中
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortRecall(i, visited, stk);
// 初始化距离
for (int i = 0; i < V; i++)
dist[i] = INF;
dist[s] = 0;
// 按照拓扑排序的顺序处理 各个顶点
while (stk.empty() == false)
{
// 获得拓扑排序的下一个顶点
int u = stk.top();
stk.pop();
// 更新所有相邻的顶点
list<AdjListNode>::iterator i;
if (dist[u] != INF)
{
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (dist[i->getV()] > dist[u] + i->getWeight())
dist[i->getV()] = dist[u] + i->getWeight();
}
}
// 打印结果
for (int i = 0; i < V; i++)
(dist[i] == INF)? cout << "INF ": cout << dist[i] << " ";
}
// 测试
int main()
{
Graph g(6);
g.addEdge(0, 1, 5);
g.addEdge(0, 2, 3);
g.addEdge(1, 3, 6);
g.addEdge(1, 2, 2);
g.addEdge(2, 4, 4);
g.addEdge(2, 5, 2);
g.addEdge(2, 3, 7);
g.addEdge(3, 4, -1);
g.addEdge(4, 5, -2);
int s = 1;
cout << "Following are shortest distances from source " << s <<" \n";
g.shortestPath(s);
return 0;
}时间复杂度
拓扑排序的时间复杂度是O(V + E)。找到拓扑顺序后,算法依次处理所有顶和其相邻顶点的顶点。总相邻顶点的个数是O(E)。因此,内循环运行O(V + E)。所以,这个算法的总体时间复杂度是O(V + E)。































 463
463

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








