红黑树的简单实现-RBTree

红黑树是一个被广泛运用的平衡二叉树，同时满足以下规则
1.每个节点不是红色就是黑色
2.根节点为黑
3.不存在连续红节点
4.每条路径上黑色节点数相等，（空节点视为黑色）
这样一来，红黑树可以保持最长路径不超过最短路径的两倍，保持近似平衡，搜索时间复杂度是O(lgN)

下面是红黑树调节节点平衡与颜色的简介，当插入节点后出现连续红节点后，判断叔叔是否存在和叔叔的颜色，
若是叔叔存在且颜色为红时

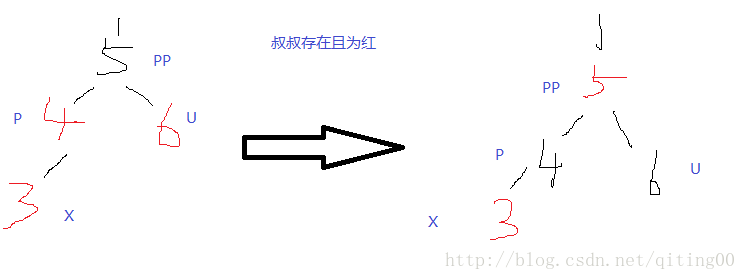
叔叔不存在 或者 叔叔存在且颜色为黑时，如下图调整，四种情况四种旋转

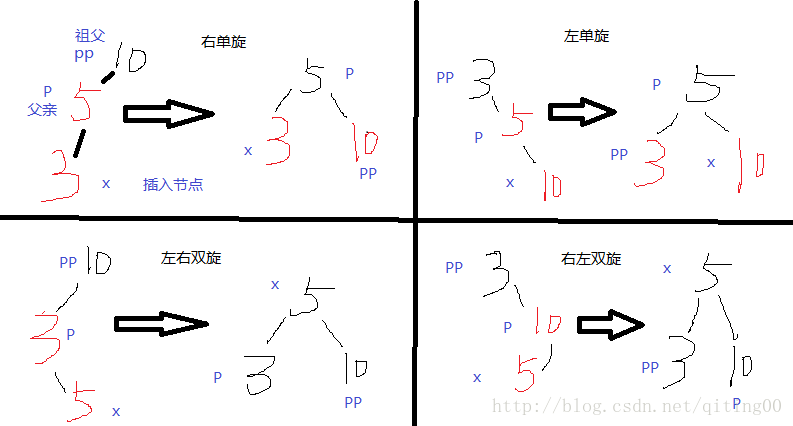
下面是实现代码：

#include <iostream>
using namespace std;


enum Color
{
    RED,
    BLACK
};
template <class T>
struct RBTreeNode
{
    RBTreeNode<T>* _left;
    RBTreeNode<T>* _right;
    RBTreeNode<T>* _parent;
    Color _color;
    T _key;

    RBTreeNode(T key)
        :_left(NULL),
        _right(NULL),
        _parent(NULL),
        _color(RED),
        _key(key)
    {}
};

template <class T>
class RBTree
{
    typedef RBTreeNode<T> Node;
public:
    RBTree()
        :_root(NULL)
    {}
    void RotateR(Node* parent)
    {
        Node* subL = parent->_left;
        Node* PParent = parent->_parent;
        Node* subLR = subL->_right;

        parent->_left = subLR;
        subL->_right = parent;
        parent->_parent = subL;
        if (subLR)
        {
            subLR->_parent = parent;
        }
        if (PParent==NULL)
        {
            _root = subL;
            subL->_parent = NULL;
        }
        else if (PParent->_key > parent->_key)
        {
            subL->_parent = PParent;
            PParent->_left = subL;
        }
        else if (PParent->_key < parent->_key)
        {
            subL->_parent = PParent;
            PParent->_right = subL;
        }

    }
    void RotateL(Node* parent)
    {
        Node* PParent = parent->_parent;
        Node* subR = parent->_right;
        Node* subRL = subR->_left;

        parent->_right = subRL;
        subR->_left = parent;
        parent->_parent = subR;
        if (subRL)
        {
            subRL->_parent = parent;
        }
        if (PParent == NULL)
        {
            _root = subR;
            subR->_parent = NULL;
        }
        else if (PParent->_key > parent->_key)
        {
            subR->_parent = PParent;
            PParent->_left = subR;
        }
        else if (PParent->_key < parent->_key)
        {
            subR->_parent = PParent;
            PParent->_right = subR;
        }

    }
    bool Insert(const T& key)
    {
        if (_root == NULL)//空树直接插入
        {
            _root = new Node(key);
            _root->_color = BLACK;
            return true;
        }
        Node* cur = _root;//非空 从根节点开始 向下找位置
        Node* parent = NULL;
        while (cur)
        {
            if (key == cur->_key)
            {
                return false;
            }
            else if (key < cur->_key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else if (key>cur->_key)
            {
                parent = cur;
                cur = cur->_right;
            }
        }

        cur = new Node(key);
        cur->_parent = parent;

        if (parent->_key > key)
        {
            parent->_left = cur;
        }
        else if (parent->_key < key)
        {
            parent->_right = cur;
        }

        //调节节点颜色
        while (parent&&parent->_color == RED)
        {
            Node* PParent = parent->_parent;
            if (PParent->_left == parent)//父亲是祖父的左
            {
                Node* uncle = PParent->_right;
                if (uncle&&uncle->_color == RED)//叔叔为红
                {
                    parent->_color = uncle->_color = BLACK;
                    PParent->_color = RED;
                    cur = PParent;
                    parent = cur->_parent;
                }
                else//叔叔不存在  或者叔叔为黑
                {
                    if (cur == parent->_left)
                    {
                        //右单旋
                        RotateR(PParent);
                        PParent->_color = RED;//祖父变红
                        parent->_color = BLACK;//父亲变黑
                    }
                    else//左右双旋
                    {
                        RotateL(parent);
                        RotateR(PParent);
                        PParent->_color = RED;//祖父 变红
                        cur->_color = BLACK;//当前节点变黑
                    }
                }
            }
            else if (PParent->_right == parent)//父亲是祖父的右
            {
                Node* uncle = PParent->_left;
                if (uncle&&uncle->_color == RED)//叔叔为红
                {
                    parent->_color = uncle->_color = BLACK;
                    PParent->_color = RED;
                    cur = PParent;
                    parent = cur->_parent;
                }
                else//叔叔不存在  或者叔叔为黑
                {
                    if (cur == parent->_right)//cur为父亲的右 左单旋
                    {
                        RotateL(PParent);//左单旋
                        parent->_color = BLACK;//父亲变红
                        PParent->_color = RED;//祖父变黑
                    }
                    else
                    {
                        //右左双旋
                        RotateR(parent);
                        RotateL(PParent);
                        cur->_color = BLACK;
                        PParent->_color = RED;
                    }
                }
            }_root->_color = BLACK;

        }return true;

    }

    void Printf()
    {
        _printf(_root);
    }
    void _printf(Node*& root)
    {
        if (root == NULL)
            return;
        _printf(root->_left);
        printf("%d  ",root->_key);
        _printf(root->_right);
    }
protected:
    Node* _root;
};


int main()
{
    int a[] = {3,2,4,5,7,9,8,0,12,13,15};
    /*int a[] = { 10,5,3 };*/
    /*int a[] = { 10,5,8 };*/
    /*int a[] = { 3,5,10 };*/
    /*int a[] = { 3,10,5};*/
    RBTree<int> t;
    for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
        t.Insert(a[i]);
    t.Printf();
    system("pause");
    return 0;
}

结果如下

如有不足 ，请不吝赐教