假如你有一张地图,地图上给出了每一对相邻城市的距离,从一个地点到另外一个地点,如何找到一条最短的路?最短路算法要解决的就是这类问题。定义:给定一个有(无)向图,每一条边有一个权值 w,给定一个起始点 S 和终止点 T ,求从 S 出发走到 T 的权值最小路径,即为最短路径。最短路算法依赖一种性质:一条两顶点间的最短路径包含路径上其他最短路径。简单的说就是:最短路径的子路径是最短路径。这个用反证法很好证明。
一、松弛技术(Relaxation)
了解最短路算法前,必须先了解松弛技术, 为什么叫松弛,有特定原因,有兴趣可以去查查相关资料,如果简化理解松弛技术,它本质上就是一个贪心操作。松弛操作:对每个顶点v∈V,都设置一个属性d[v],用来描述从源点 s 到 v 的最短路径上权值的上界,成为最短路径估计(Shortest-path Estimate),同时π[v]代表前趋。初始化伪代码:
INITIALIZE-SINGLE-SOURCE(G, s)
for each vertex v ∈ V[G]
do d[v] ← ∞ //距离
π[v] ← NIL //是否遍历过
d[s] ← 0
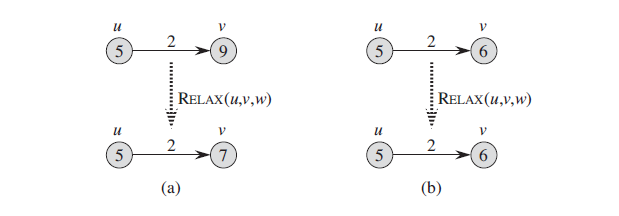
初始化之后,对所有 v∈V,π[v] = NIL,对v∈V – {s},有 d[s] = 0 以及 d[v] = ∞。松弛一条边(u, v),如果这条边可以对最短路径改进,则更新 d[v] 和π[v] 。一次松弛操作可以减小最短路径估计的值 d[v] ,并更新 v 的前趋域π[v]。下面的伪代码对边(u,v)进行了一步松弛操作:
RELAX(u, v, w)
if d[v] > d[u] + w(u, v)
then d[v] ← d[u] + w(u, v)
π[v] ← u上边的图示中,左边例子,最短路径估计值减小,右边例子,最短路径估计值不变。当发现 v 到 u 有更近的路径时,更新 d[v] 和π[v] 。
二、Dijkstra算法
解决最短路问题,最经典的算法是 Dijkstra算法,它是一种单源最短路算法,其核心思想是贪心算法(Greedy Algorithm),Dijkstra算法由荷兰计算机科学家Dijkstra发现,这个算法至今差不多已有50年历史,但是因为它的稳定性和通俗性,到现在依然强健。另外,Dijkstra算法要求所有边的权值非负。
Dijkstra算法思想为:设 G = (V, E) 是一个带权有向图,把图中顶点集合 V 分成两组,第一组为已求出最短路径的顶点集合(用 S 表示,初始时 S 中只有一个源点,以后每求得一条最短路径 , 就将其加入到集合 S 中,直到全部顶点都加入到 S 中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用 U 表示),按最短路径长度的递增次序依次把第二组的顶点加入 S 中。在加入的过程中,总保持从源点 v 到 S 中各顶点的最短路径长度不大于从源点 v 到 U 中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S 中的顶点的距离就是从 v 到此顶点的最短路径长度,U 中的顶点的距离,是从 v 到此顶点只包括 S 中的顶点为中间顶点的当前最短路径长度。 (在实际的实现中只用一个布尔数组,true表示在S中,false表示在U中)伪代码:(维基百科版):
u := Extract_Min(Q) 在顶点集合 Q 中搜索有最小的 d[u] 值的顶点 u。这个顶点被从集合 Q 中删除并返回给用户。
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity
4 previous[v] := undefined
5 d[s] := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijkstra演算法主體
9 u := Extract_Min(Q)
10 S := S union {u}
11 for each edge (u,v) outgoing from u
12 if d[v] > d[u] + w(u,v) // 拓展边(u,v)
13 d[v] := d[u] + w(u,v)
14 previous[v] := u
如果我们只对在 s 和 t 之间寻找一条最短路径的话,我们可以在第9行添加条件如果满足 u = t 的话终止程序。现在我们可以通过迭代来回溯出 s 到 t 的最短路径:
1 s := empty sequence
2 u := t
3 while defined u
4 insert u to the beginning of S
5 u := previous[u]
现在序列 S 就是从 s 到 t 的最短路径的顶点集.
(算法导论版)
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G]
4 while Q ≠ Ø
5 do u ←EXTRACT-MIN(Q)
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w)
第 1 行将 d 和 π 初始化,第 2 行初始化集合 S 为空集,4 ~ 8 行每次迭代,都从 U 中选取一个点加入到 S 中,然后所有的边进行松弛操作,即每次迭代,整个图的 d 和π 都更新一遍。过程本身很简单,下边是图示:
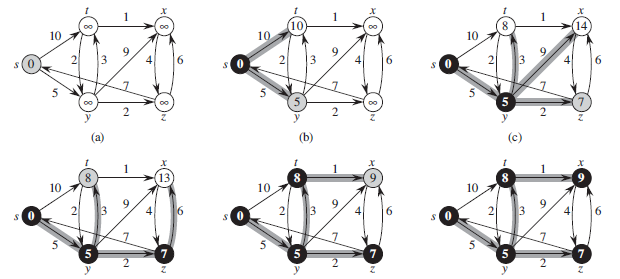
源点 s 是最左端顶点。最短路径估计被标记在顶点内,阴影覆盖的边指出了前趋的值。黑色顶点在集合 S中,而白色顶点在最小优先队列 Q = V – S 中。a) 第 4 ~ 8 行 while 循环第一次迭代前的情形。阴影覆盖的顶点具有最小的 d 值,而且在第 5 行被选为顶点 u 。b) ~ f) while 循环在第一次连续迭代后的情形。每个图中阴影覆盖的顶点被选作下一次迭代第 5 行的顶点 u。f) 图中的 d 和π 值是最终结果。
Dijkstra算法时间主要消耗在寻找最小权值的边,和松弛所有剩余边,所以 EXTRACT-MIN(Q) 这一步,更好的方法是使用优先队列,优先队列可以用二叉堆,斐波那契堆等来实现,下面的代码,我用库自带的优先队列,经这样改造后,效率还是很可观的。
理解最短路算法,最基础,最简单,最经典的要数这个题目:HDU 2544 最短路,纯粹的算法练习题,用Dijkstra,我写了三个代码来实现。
1)邻接矩阵 + Dijkstra,最简单的方式,当然也是最好理解的方式:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <climits>
int map2544[105][105];
bool mark2544[105];
int dist2544[105];
int N2544,M2544;//顶点、边
void init2544()
{
for(int i=0;i<105;++i)
for(int j=0;j<105;++j)
map2544[i][j]=INT_MAX>>1;
}
void Dijkstra1(int src)//临接矩阵
{
for(int i=1;i<=N2544;++i)
{
dist2544[i]=map2544[src][i];
mark2544[i]=false;
}
dist2544[src]=0;
for(int i=1;i<=N2544;++i)
{
if(mark2544[i]) continue;
int min=INT_MAX >> 1,k=src;
for(int j=1;j<=N2544;++j)
{
if(!mark2544[j] && dist2544[j]<min)
{
min=dist2544[j],k=j;
}
}
mark2544[k]=true;
for(int i=1;i<=N2544;++i)
{
if(!mark2544[i] && dist2544[k]+map2544[k][i]<dist2544[i])
dist2544[i]=dist2544[k]+map2544[k][i];
}
}
}
void Dijkstra2(int src)//临接矩阵
{
for(int i=1;i<=N2544;++i)
{
dist2544[i]=map2544[src][i];
mark2544[i]=false;
}
dist2544[src]=0;
for(;;)
{
int min=INT_MAX>>1,k=src;
for(int j=1;j<=N2544;++j)
{
if(!mark2544[j] && dist2544[j]<min)
{
min=dist2544[j],k=j;
}
}
if(min == INT_MAX>>1) break;
mark2544[k]=true;
for(int i=1;i<=N2544;++i)
{
if(!mark2544[i] && dist2544[k]+map2544[k][i]<dist2544[i])
dist2544[i]=dist2544[k]+map2544[k][i];
}
}
}
int main()
{
freopen("in.txt","r",stdin);
while(scanf("%d%d",&N2544,&M2544))
{
if(N2544==0 && M2544==0) break;
init2544();
int A,B,C;
for(int i=0;i<M2544;++i)
{
scanf("%d %d %d",&A,&B,&C);
map2544[A][B]=map2544[B][A]=C;
}
Dijkstra2(1);
printf("%d\n",dist2544[N2544]);
}
return 0;
}2)邻接表 + 优先队列优化 +Dijkstra,效率更高,更实用的方式:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <climits>
#include <queue>
using namespace std;
#define MAXLEN 102 // 最大顶点数为10
int N2544,M2544;//顶点、边
int dist2544[MAXLEN];
bool mark2544[MAXLEN];
typedef struct node{ // 边表结点
node(){ next=NULL; }
int adjvex; // 邻接点域
int info; //数据域info
struct node *next; // 指向下一个邻接点的指针域
}EdgeNode;
typedef struct vnode{ // 顶点表结点
vnode(){ firstedge=NULL; }
int vertex; // 顶点域
EdgeNode *firstedge; // 边表头指针
}VertexNode;
typedef VertexNode AdjList[MAXLEN]; // AdjList是邻接表类型
typedef struct{
AdjList adjlist; // 接表
int n,e; // 顶点数和边数
}ALGraph; // ALGraph是以邻接表方式存储的图类型
ALGraph G;//此处发现如果在函数中传递G的指针式,HDU中一直WA,估计和传递参数有关,具体解释请看《高质量C/C++指南》中7.4节
int top=0;
EdgeNode node2544[20005];
EdgeNode* GetNode2544()
{
return node2544+top++;
}
bool CreateGraphAL ()
{
int A,B,C;
EdgeNode * s;
scanf("%d%d",&(G.n),&(G.e)); // 读入顶点数和边数
N2544=G.n,M2544=G.e;
if(G.n==0 && G.e==0) return true;
for (int k=0;k<G.e;k++) // 建立边表
{
scanf("%d %d %d",&A,&B,&C); // 读入边<Vi,Vj>的顶点对应序号
//s=new EdgeNode; // 生成新边表结点s
s=GetNode2544();
s->adjvex=B; // 邻接点序号为j
s->info=C; // 边的权重
s->next=G.adjlist[A].firstedge; // 将新边表结点s插入到顶点Vi的边表头部
G.adjlist[A].firstedge=s;
//s=new EdgeNode; // 生成新边表结点s
s=GetNode2544();
s->adjvex=A; // 邻接点序号为j
s->info=C; // 边的权重
s->next=G.adjlist[B].firstedge; // 将新边表结点s插入到顶点Vi的边表头部
G.adjlist[B].firstedge=s;
}
return false;
}
void init2544()
{
for(int i=1;i<=G.n;++i)
G.adjlist[i].firstedge=NULL;
for(int i=0;i<20005;++i)
node2544[i].next=NULL;
top=0;
}
struct cmpnode {
int v, dis;
cmpnode () {}
cmpnode (int V, int DIS) : v(V), dis(DIS) {}
friend bool operator < (const cmpnode a, const cmpnode b) {
return a.dis > b.dis;
}
};
void Dijkstra3(int src)
{
priority_queue<cmpnode> q;
cmpnode first;
for(int i=1;i<=N2544;++i)
{
dist2544[i]=INT_MAX>>1;
mark2544[i]=false;
}
dist2544[src]=0;
q.push(cmpnode(src,0));
while(!q.empty())
{
first=q.top();q.pop();
mark2544[first.v]=true;
EdgeNode *s;
s=G.adjlist[first.v].firstedge;
while(s!=NULL)
{
if(!mark2544[s->adjvex] && first.dis+s->info < dist2544[s->adjvex])//第一个bool判断能成立的原因,边中没有负值,所以根据贪心第一次遍历到的时候距离最短
{
dist2544[s->adjvex]=first.dis+s->info;
q.push(cmpnode(s->adjvex,dist2544[s->adjvex]));
}
s=s->next;
}
}
}
int main()
{
freopen("in.txt","r",stdin);
while(1)
{
init2544();
if(CreateGraphAL()) break;
Dijkstra3(1);
printf("%d\n",dist2544[N2544]);
}
return 0;
}如果对Dijkstra算法核心思想不是很理解,可能会问:Dijkstra算法为什么不能处理负权边?
Dijkstra由于是贪心的,每次都找一个距源点最近的点(dmin),然后将该距离定为这个点到源点的最短路径(d[i] ← dmin);但如果存在负权边,那就有可能先通过并不是距源点最近的一个次优点(dmin’),再通过这个负权边 L (L < 0),使得路径之和更小(dmin’ + L < dmin),则 dmin’ + L 成为最短路径,并不是dmin,这样Dijkstra就被囧掉了。(总结一句话:由于次优点的距离已经大于最有优点,所以就算加上负值小于最优解也不对)比如n = 3,邻接矩阵:
0, 3, 4
3, 0,-2
4,-2, 0
用Dijkstra求得 d[1,2] = 3,事实上 d[1,2] = 2,就是通过了 1-3-2 使得路径减小。Dijkstra的贪心是建立在边都是正边的基础上,这样,每次往前推进,路径长度都是变大的,如果出现负边,那么先前找到的最短路就不是真正的最短路,比如上边的例子,这个算法也就算废了。
另外,Dijkstra算法时间复杂度为O(V2 +E)。源点可达的话,O(V * lgV + E * lgV) => O(E * lgV)。当是稀疏图的情况时,此时 E = V2/lgV,所以算法的时间复杂度可为 O(V2)。若是斐波那契堆作优先队列的话,算法时间复杂度为O(V * lgV + E)。
参考文献:
http://www.cppblog.com/doer-xee/archive/2009/11/26/101972.aspx 参考普通的Dijkstra、优先队列优化的Dijkstra、 堆优化的Dijkstra的代码
http://mindlee.net/2011/11/18/shortest-paths-algorithm/ 参考各种最近距离的计算方法
http://blog.csdn.net/v_JULY_v/article/details/6096981 结构之法,参考效率分析部分

























 619
619

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








