1.BIRCH算法概念
BIRCH(Balanced Iterative Reducing and Clustering Using Hierarchies)全称是:利用层次方法的平衡迭代规约和聚类。BIRCH算法是1996年由Tian Zhang提出来的,参考文献1。首先,BIRCH是一种聚类算法,它最大的特点是能利用有限的内存资源完成对大数据集的高质量的聚类,同时通过单遍扫描数据集能最小化I/O代价。
首先解释一下什么是聚类,从统计学的观点来看,聚类就是给定一个包含N个数据点的数据集和一个距离度量函数F(例如计算簇内每两个数据点之间的平均距离的函数),要求将这个数据集划分为K个簇(或者不给出数量K,由算法自动发现最佳的簇数量),最后的结果是找到一种对于数据集的最佳划分,使得距离度量函数F的值最小。从机器学习的角度来看,聚类是一种非监督的学习算法,通过将数据集聚成n个簇,使得簇内点之间距离最小化,簇之间的距离最大化。
BIRCH算法特点:
(1)BIRCH试图利用可用的资源来生成最好的聚类结果,给定有限的主存,一个重要的考虑是最小化I/O时间。
(2)BIRCH采用了一种多阶段聚类技术:数据集的单边扫描产生了一个基本的聚类,一或多遍的额外扫描可以进一步改进聚类质量。
(3)BIRCH是一种增量的聚类方法,因为它对每一个数据点的聚类的决策都是基于当前已经处理过的数据点,而不是基于全局的数据点。
(4)如果簇不是球形的,BIRCH不能很好的工作,因为它用了半径或直径的概念来控制聚类的边界。
BIRCH算法中引入了两个概念:聚类特征和聚类特征树,以下分别介绍。
1.1 聚类特征(CF)
CF是BIRCH增量聚类算法的核心,CF树中得节点都是由CF组成,一个CF是一个三元组,这个三元组就代表了簇的所有信息。给定N个d维的数据点{x1,x2,....,xn},CF定义如下:
CF=(N,LS,SS)
其中,N是子类中节点的数目,LS是N个节点的线性和,SS是N个节点的平方和。
CF有个特性,即可以求和,具体说明如下:CF1=(n1,LS1,SS1),CF2=(n2,LS2,SS2),则CF1+CF2=(n1+n2, LS1+LS2, SS1+SS2)。
例如:
假设簇C1中有三个数据点:(2,3),(4,5),(5,6),则CF1={3,(2+4+5,3+5+6),(2^2+4^2+5^2,3^2+5^2+6^2)}={3,(11,14),(45,70)},同样的,簇C2的CF2={4,(40,42),(100,101)},那么,由簇C1和簇C2合并而来的簇C3的聚类特征CF3计算如下:
CF3={3+4,(11+40,14+42),(45+100,70+101)}={7,(51,56),(145,171)}
另外在介绍两个概念:簇的质心和簇的半径。假如一个簇中包含n个数据点:{Xi},i=1,2,3...n.,则质心C和半径R计算公式如下:
C=(X1+X2+...+Xn)/n,(这里X1+X2+...+Xn是向量加)
R=(|X1-C|^2+|X2-C|^2+...+|Xn-C|^2)/n
其中,簇半径表示簇中所有点到簇质心的平均距离。CF中存储的是簇中所有数据点的特性的统计和,所以当我们把一个数据点加入某个簇的时候,那么这个数据点的详细特征,例如属性值,就丢失了,由于这个特征,BIRCH聚类可以在很大程度上对数据集进行压缩。
1.2 聚类特征树(CF tree)
CF tree的结构类似于一棵B-树,它有两个参数:内部节点平衡因子B,叶节点平衡因子L,簇半径阈值T。树中每个节点最多包含B个孩子节点,记为(CFi,CHILDi),1<=i<=B,CFi是这个节点中的第i个聚类特征,CHILDi指向节点的第i个孩子节点,对应于这个节点的第i个聚类特征。例如,一棵高度为3,B为6,L为5的一棵CF树的例子如图所示:
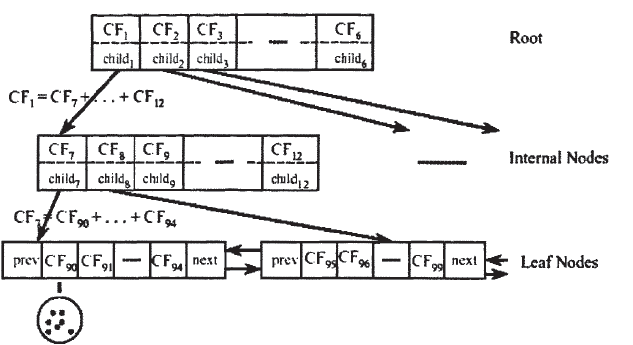
一棵CF树是一个数据集的压缩表示,叶子节点的每一个输入都代表一个簇C,簇C中包含若干个数据点,并且原始数据集中越密集的区域,簇C中包含的数据点越多,越稀疏的区域,簇C中包含的数据点越少,簇C的半径小于等于T。随着数据点的加入,CF树被动态的构建,插入过程有点类似于B-树。加入算法表示如下:
(1)从根节点开始,自上而下选择最近的孩子节点
(2)到达叶子节点后,检查最近的元组CFi能否吸收此数据点
是,更新CF值
否,是否可以添加一个新的元组
是,添加一个新的元组
否则,分裂最远的一对元组,作为种子,按最近距离重新分配其它元组
(3)更新每个非叶节点的CF信息,如果分裂节点,在父节点中插入新的元组,检查分裂,直到root
计算节点之间的距离函数有多种选择,常见的有欧几里得距离函数和曼哈顿距离函数,具体公式如下:
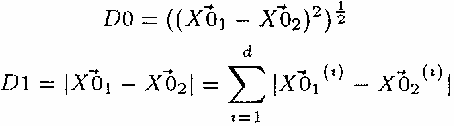
构建CF树的过程中,一个重要的参数是簇半径阈值T,因为它决定了CF tree的规模,从而让CF tree适应当前内存的大小。如果T太小,那么簇的数量将会非常的大,从而导致树节点数量也会增大,这样可能会导致所有数据点还没有扫描完之前内存就不够用了。
2.算法流程
BIRCH算法流程如下图所示:
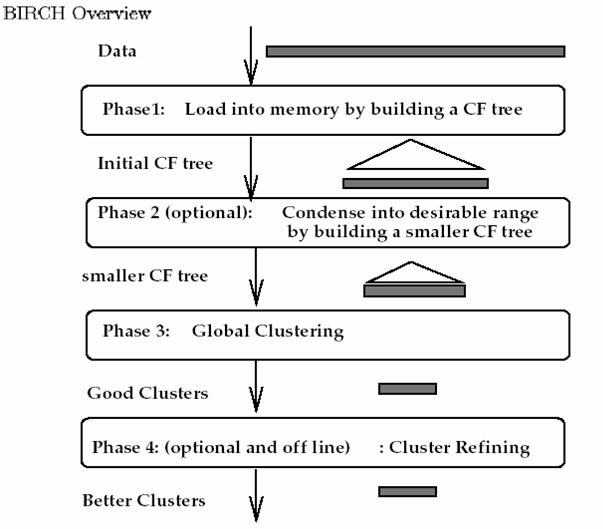
整个算法的实现分为四个阶段:
(1)扫描所有数据,建立初始化的CF树,把稠密数据分成簇,稀疏数据作为孤立点对待
(2)这个阶段是可选的,阶段3的全局或半全局聚类算法有着输入范围的要求,以达到速度与质量的要求,所以此阶段在阶段1的基础上,建立一个更小的CF树
(3)补救由于输入顺序和页面大小带来的分裂,使用全局/半全局算法对全部叶节点进行聚类
(4)这个阶段也是可选的,把阶段3的中心点作为种子,将数据点重新分配到最近的种子上,保证重复数据分到同一个簇中,同时添加簇标签
详细流程请参考文献1。
3.算法实现
BIRCH算法的发明者于1996年完成了BIRCH算法的实现,是用c++语言实现的,已在solaris下编译通过。
另外算法的实现也可参考:http://blog.sina.com.cn/s/blog_6e85bf420100om1i.html
参考文献:
1.BIRCH:An Efficient Data Clustering Method for Very Large Databases

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








