[BZOJ 1063][NOI 2008]道路设计(树形DP)

题目链接

http://www.lydsy.com/JudgeOnline/problem.php?id=1063

题面大意

给一个有$n$个结点的有根树，树根为点1，树上有若干条不相交的链，定义一个点的不便利值为它到根节点的路径上不属于链的边的个数，定义整棵树的不便利值为树中点的最大不便利值，求这棵树的最小不便利值，以及取最小值时的方案数。

思路

由题目限制任意两条链不能相交，可以发现这相当于一个点最多只能和它的两个儿子连链边。
显然对于一个点而言，只有可能在它有3个儿子的情况下，它对应的子树的不便利值取$max\{1,(子树v的不便利值)\}$，在点数$n$相同的情况下，满三叉树的不便利值是最大的，约$log_3n$。
一个不严格的证明如下：因为在儿子个数为1或2的情况下，该点到其儿子可以保证有链覆盖，当儿子个数>=3时，该点对应的子树的不便利值取$max\{1,(子树v的不便利值)\}$，而儿子个数越少，整棵树的深度就能尽量深，因此儿子个数取3时，这个点对应子树的不便利值才能尽量大。以此类推，每个点都有三个儿子(除了叶子节点)，故满三叉树的不便利值是最大的。
因此，在数据规模达到极限范围的情况下整棵树的不便利值最多为$log_3{10^5},大概是10$
10非常小，因此我们可以暴力枚举一个子树的不便利值。
用$f[u][i][j]$表示对于子树$u$,它的不便利值为$i$，它与它的$j$个儿子连边的方案数。
可以得到一个初步的DP方程：

(以上图片引自“将狼踩尽”(http://www.cnblogs.com/jianglangcaijin/archive/2013/12/06/3462328.html))

其实可以看作一个树上的计数问题。
注意到一个点能往下引多少条链边其实是有限制的，如果该点和其父亲之间的边是链边(如下图a)，那么该点只能往下引0或1条链边。反之，该点可以往下引0或1或2条链边(如下图b)。

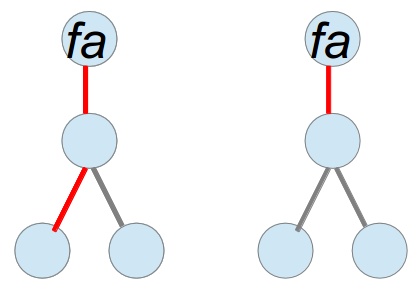
图(a)

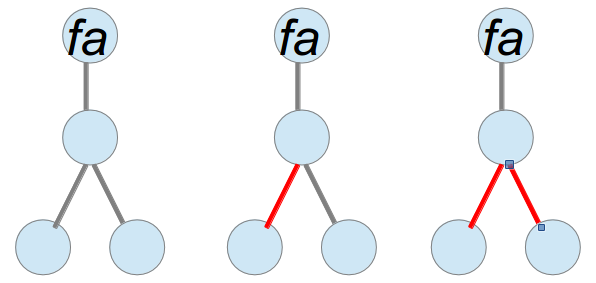
图(b)
$f[i][j][0]$的情况下，$i$的儿子的不便利值肯定要增加1，因此$f[i][j][0]就是从f[x][j-1][0...2]$转移来的($x$是$i$的儿子)
$f[i][j][1]$情况下，$i$的其中一个儿子($x$)的不便利值是不变的，这个儿子往下只能延伸1条链或者不延伸，然后其他的儿子($y$)的不便利值要增加1，它们向下走可以引出0条、1条、2条链边
$f[i][j][2]$情况下，$i$的两个儿子($x$,$y$)的不便利值是不变的，它们继续向下走只能连0或1条链边，对于其他的儿子($z$)，它们的不便利值要加1，它们继续向下走可以引0、1、2条链边。

这个公式看上去很显然，虽然用这个公式来求虽然可行，但是比较麻烦，实际上可以把这个公式化简，对于点$i$的每个儿子$x$，进行下面的操作(实际上就是将$x对i$的贡献一次性加进去)：

(以上图片引自“将狼踩尽”(http://www.cnblogs.com/jianglangcaijin/archive/2013/12/06/3462328.html))

然后有个细节需要注意：由于是模意义下的运算，再加上DP过程中有乘法操作，因此如果碰到取模以前不是0，取模以后为0的，那么标记它取模以后为模数，防止做完乘法以后，如果本来不取模答案就不是0，取模以后反而变成0了，以后再做乘法，答案还是0，导致WA。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>

#define MAXN 110000

using namespace std;

typedef long long int LL;

int n,m;
LL f[MAXN][11][3],mod;

struct edge
{
    int u,v,next;
}edges[2*MAXN];

int head[MAXN],nCount=0;

void AddEdge(int U,int V)
{
    edges[++nCount].u=U;
    edges[nCount].v=V;
    edges[nCount].next=head[U];
    head[U]=nCount;
}

LL cal(LL x)
{
    if(x&&x%mod==0) return mod;
    return x%mod;
}

void DFS(int u,int fa)
{
    for(int i=0;i<=10;i++) f[u][i][0]=1LL;
    for(int p=head[u];p!=-1;p=edges[p].next)
    {
        int v=edges[p].v;
        if(v==fa) continue;
        DFS(v,u);
        for(int j=0;j<=10;j++) //枚举子树u的最大不便利值
        {
            LL f1=cal(f[v][j][0]+f[v][j][1]);
            LL f2=0;
            if(j) f2=cal(f[v][j-1][0]+f[v][j-1][1]+f[v][j-1][2]); //!!!!!!!
            f[u][j][2]=cal(f[u][j][2]*f2+f[u][j][1]*f1);
            f[u][j][1]=cal(f[u][j][1]*f2+f[u][j][0]*f1);
            f[u][j][0]=cal(f[u][j][0]*f2);
        }
    }
}

int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%lld",&n,&m,&mod);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        AddEdge(u,v);
        AddEdge(v,u);
    }
    if(m!=n-1)
    {
        puts("-1");
        puts("-1");
        return 0;
    }
    DFS(1,-1);
    for(int i=0;i<=10;i++) //暴力枚举整个树最大不便利值的最小值
    {
        if(f[1][i][0]+f[1][i][1]+f[1][i][2]>0) //有方案
        {
            printf("%d\n",i);
            printf("%lld\n",(f[1][i][0]+f[1][i][1]+f[1][i][2])%mod);
            return 0;
        }
    }
    return 0;
}