[BZOJ 1913][APIO 2011]信号覆盖(计算几何)

题目链接

http://www.lydsy.com/JudgeOnline/problem.php?id=1913

思路

很容易发现，最终的答案为

$$\frac{每种方案在圆上和圆中的点的个数}{C_n^3(总方案数)}$$
其实我们可以无视掉确定下圆的那三个点，那么答案可以表示为
$$\frac{ans}{C_n^3(总方案数)}+3$$
圆里面只会包含1个点，那么我们可以考虑枚举由确定圆的三个点和圆里面包含的那个点所构成的四边形。对于一个确定的四边形而言，每种方案要么是给ans贡献1种方案(凹四边形)，要么是贡献2种方案(凸四边形)，为什么呢？如下图

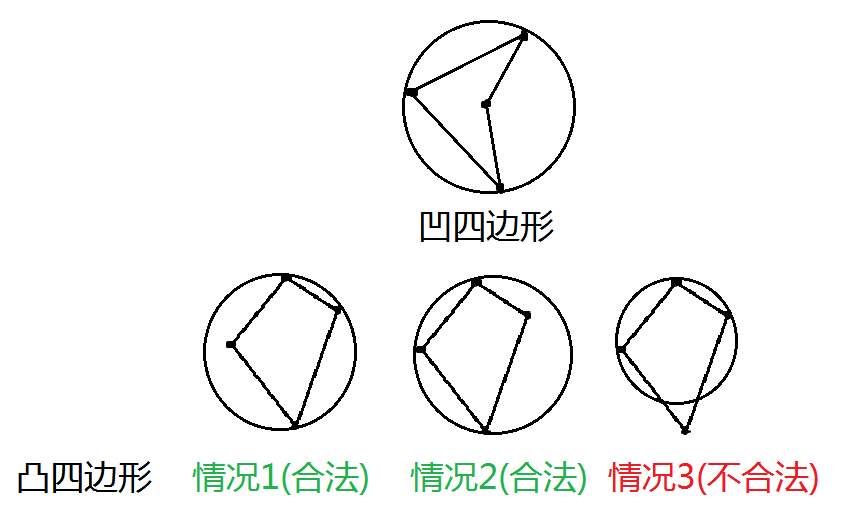
凹四边形相当于是一个三角形内包含1个点，此时只能找到一个圆，为 $ans$贡献加1
而凸四边形的情况则有4种(图中只画了3种)，由于题目限制了任意四点不共圆，因此其中只有2种是合法的，为 $ans$贡献加2
因此最终答案可以表示为
$$\frac{num_{凹四边形}+2num_{凸四边形}}{C_n^3(总方案数)}+3$$
其实 $num_{凹四边形}+num_{凸四边形}=C_n^4$，那么这两个集合中我们只要枚举其中一个集合的大小就可以了，显然凹四边形比凸四边形好枚举一些。答案简化为
$$\frac{num_{凹四边形}+2(C_n^4-num_{凹四边形})}{C_n^3(总方案数)}+3$$
考虑如何求 $num_{凹四边形}$。我们可以枚举那个被其他三个点构成的三角形覆盖的点 $x$，然后求有多少个不同的三角形覆盖了这个点，就是凹四边形的个数了。这样做还是不好求，不如求有多少个不同的三角形没有覆盖此点。我们可以以点$x$为原点构建一个坐标系，将其他的点按照极角排序，这样就能得到一个极角按逆时针顺序的 $n-1$个点的序列。如下图

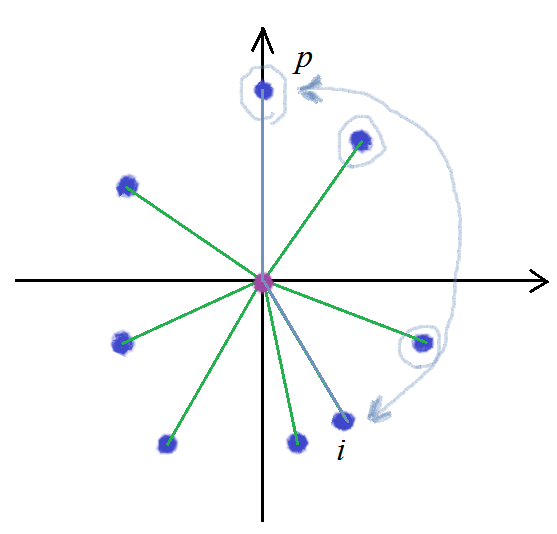
然后枚举点 $i$，找在逆时针方向上在它后面的点$p$(注意 $p$在$i$逆时针方向后面，这是为了防止重复计算)，使得点 $i+1$到 $p$的极角线夹角刚好小于$180$度，且点 $i+1$到 $p+1$的极角线夹角刚好大于 $180$度，这样的话，点 $i+1$到 $p$中选2个点，和点$i$构成的三角形显然是不覆盖点 $x$的。我们可以维护一个指针代表点$p$，按极角序枚举点 $i$，这样就能在线性时间内求出不覆盖点$x$的所有三角形个数。

代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <cmath>

#define MAXN 110000
#define PI 3.1415926535897384626

using namespace std;

typedef long long int LL;

int n;

struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y):x(_x),y(_y){}
}points[MAXN],tmp[MAXN];

int top=0;

Point operator-(Point a,Point b)
{
    return Point(a.x-b.x,a.y-b.y);
}

double cross(Point a,Point b)
{
    return a.x*b.y-a.y*b.x;
}

double ang[MAXN];

LL C(LL n,LL m)
{
    if(m==1) return n;
    if(m==2) return n*(n-1)/2;
    if(m==3) return n*(n-1)*(n-2)/6;
    return n*(n-1)*(n-2)*(n-3)/24;
}

LL ans=0; //ans=凹多边形个数

void calc(int x) //以点x为原点，找没有覆盖点x的三角形个数
{
    top=0; //!!!!!
    for(int i=1;i<=n;i++)
        if(i!=x)
            ang[++top]=atan2((points[i]-points[x]).y,(points[i]-points[x]).x);
    sort(ang+1,ang+top+1);
    LL tot=0; //tot=没有盖住点x的三角形个数
    int t=top;
    for(int i=1;i<=t;i++)
        ang[++top]=ang[i]+2*PI; //让负极角复制一遍变成正的
    int p=1; //x->i和x->p所夹的夹角小于等于2PI
    for(int i=1;i<=t;i++)
    {
        p=max(p,i+1);
        while(p<=top&&ang[p]<ang[i]+PI) p++;
        if(p-i-1>=2) tot+=C(p-i-1,2);
    }
    ans+=C(n-1,3)-tot;
}

int main()
{
    scanf("%d",&n);
    if(n<=3) { printf("0\n"); return 0; }
    for(int i=1;i<=n;i++)
        scanf("%lf%lf",&points[i].x,&points[i].y);
    for(int i=1;i<=n;i++)
        calc(i);
    LL ao=ans,tu=C(n,4)-ao; //ao=凹多边形个数，tu=凸多边形个数
    printf("%lf\n",(double)(ao+2*tu)/C(n,3)+3); //!!!!!
    return 0;
}