A. 填填填
题目
题目描述:
输入格式:
输出格式:
样例输入:
3
0 3 0
2 0 0
样例输出:
2
数据范围:

时间限制:
0.2s
空间限制:
512MB
思路
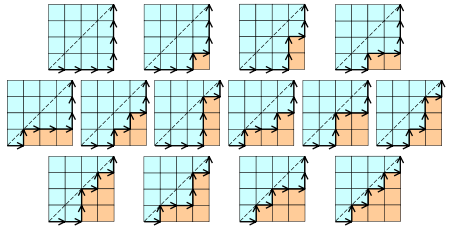
此题来自于2014年百度之星初赛的Grids一题。原题目没有在初始的空格里填入任何数字,答案为 catalan(n) 。
为什么呢?注意到,前
i
个数字一定是填在最前面的列里(如果有数字填在后面,最前面的列里不是连续的,有空格的话,之后只能用大于
?????0000
???000000
这非常类似于catalan数里的一个模型:给你一个
(似乎扯远了。。。不过补充一下原题的解法,对做出这个题还是有好处的)
此题由于已经填入了某些数字,因此单纯用组合数学来解决此题是不行的。考虑DP,用
f[i][j](j>=⌊i+12⌋)
来表示数字
1
到
其实也就是对原题的DP解法,加上一些限制而已。
然后此题最丧病的地方要数高精度了,此题时限太小,很容易卡时,因此需要卡常数写个比较快的压位高精才行
代码
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#define MAXN 1000 //数字长度
#define SYS 1000000000000000000LL //进制
using namespace std;
typedef long long int LL;
struct Hugeint //高精度
{
LL s[60];
int siz; //数字大小
Hugeint()
{
siz=0;
memset(s,0,sizeof(s));
}
Hugeint operator + (Hugeint b) //高精度加法
{
int i,j;
Hugeint out;
out.siz=max(siz,b.siz);
for(i=1;i<=out.siz;i++)
{
out.s[i]+=s[i]+b.s[i];
if(out.s[i]>=SYS)
{
out.s[i+1]++;
out.s[i]-=SYS;
}
}
if(out.s[out.siz+1]!=0)
{
out.siz++;
}
return out;
}
void print() //输出
{
int i;
if(!siz)
{
printf("0");
return;
}
printf("%lld",s[siz]);
for(i=siz-1;i>=1;i--)
{
printf("%018lld",s[i]);
}
}
}f[2][1100];
int mp[2][1100];
pair<int,int>pos[2200];
int n;
int main()
{
scanf("%d",&n);
for(int i=1;i<=2;i++)
{
for(int j=1;j<=n;j++)
{
int x;
scanf("%d",&x);
if(x)
{
pos[x]=make_pair(i,j);
}
}
}
f[0][0].siz=1;
f[0][0].s[1]=1;
int now=1,pre=0;
for(int i=1;i<=2*n;i++)
{
memset(f[now],0,sizeof(f[now]));
for(int j=(i+1)>>1;j<=i&&j<=n;j++)
{
if(pos[i]==make_pair(0,0))
f[now][j]=f[pre][j-1]+f[pre][j];
else
{
if(pos[i]==make_pair(1,j))
f[now][j]=f[pre][j-1];
else if(pos[i]==make_pair(2,i-j))
f[now][j]=f[pre][j];
}
}
swap(now,pre);
}
f[pre][n].print();
return 0;
}B. 线线线
题目
题目描述:
输入格式:
输出格式:
样例输入:
8
3 3
3 1
9 1
7 4
10 4
4 5
1 6
5 9
8 8
样例输出:
4.472
数据范围:

时间限制:
5s
空间限制:
512MB
思路
我的做法就是直接三分穿过点
p
<script type="math/tex" id="MathJax-Element-3422">p</script>的直线的极角。。。
不太好造数据卡三分,但是jcvb的数据还是比较刁,炸了我三分的精度。。。
这个题三分EPS要设1e-13才行,刚开始我设1e-6只有10分,非常悲剧。。
代码
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <cmath>
#define MAXN 220000
#define PI 3.1415926535897384626
#define EPS 1e-13
using namespace std;
typedef long double LD;
struct Point
{
double x,y;
Point(){}
Point(double _x,double _y):x(_x),y(_y){}
}points[MAXN],p;
int n;
Point operator-(Point a,Point b)
{
return Point(a.x-b.x,a.y-b.y);
}
Point operator+(Point a,Point b)
{
return Point(a.x+b.x,a.y+b.y);
}
double cross(Point a,Point b)
{
return a.x*b.y-a.y*b.x;
}
double dist(Point a,Point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
struct Line
{
Point st,ed;
Line(){}
Line(Point _st,Point _ed):st(_st),ed(_ed){}
};
double dist(Line a,Point b)
{
return fabs(cross(b-a.st,a.ed-a.st))/dist(a.ed,a.st);
}
double calc(double ang)
{
Line t=Line(p,p+Point(cos(ang),sin(ang)));
double maxdis=0;
for(int i=1;i<=n;i++)
maxdis=max(maxdis,dist(t,points[i]));
return maxdis;
}
int main()
{
scanf("%d",&n);
scanf("%lf%lf",&p.x,&p.y);
for(int i=1;i<=n;i++)
scanf("%lf%lf",&points[i].x,&points[i].y);
double lowerBound=0,upperBound=PI;
while(fabs(upperBound-lowerBound)>EPS)
{
double mid1=lowerBound+(upperBound-lowerBound)/3;
double mid2=upperBound-(upperBound-lowerBound)/3;
if(calc(mid1)<calc(mid2))
upperBound=mid2;
else lowerBound=mid1;
}
double ans=1e20;
double L=max((double)0,lowerBound-0.05),R=min(PI,upperBound+0.05);
ans=min(ans,calc((lowerBound+upperBound)/2));
double mint=(lowerBound+upperBound)/2;
for(double t=L;t<=R;t+=0.001)
{
if(ans>calc(t))
{
ans=calc(t);
mint=t;
}
}
L=max((double)0,mint-0.005),R=min(PI,mint+0.005);
for(double t=L;t<=R;t+=0.0001)
{
if(ans>calc(t))
{
ans=calc(t);
mint=t;
}
}
long long int t=ans*1000;
printf("%.3lf",(double)t/1000);
return 0;
}C. 凸凸凸
题目
题目描述:
输入格式:

输出格式:
样例输入:
9 7
1 1
1 3
3 3
3 1
6 5
6 6
7 3
3
0 4 0 4
2 7 0 7
3 7 3 6
样例输出:
4.0
10.0
6.0
数据范围:
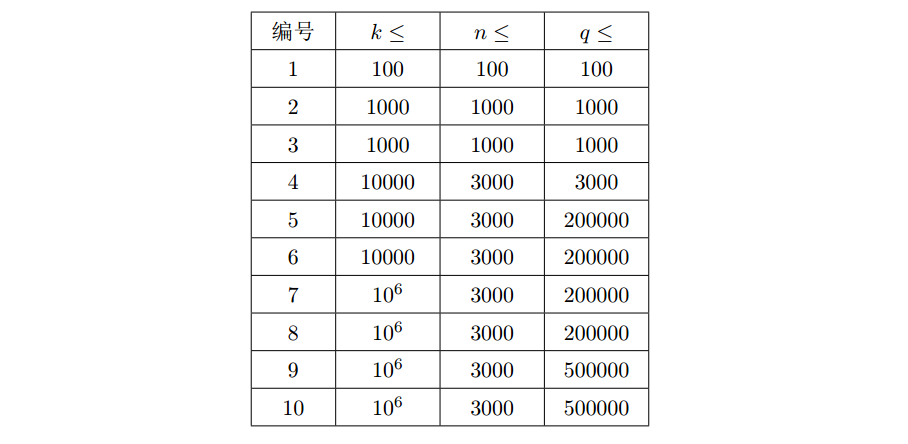
时间限制:
5s
空间限制:
512MB
思路
我不会写标解。。。直接打了40分的裸暴力
代码
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#define MAXN 11000
using namespace std;
typedef long long int LL;
__attribute__((optimize("-O2")))
int n,k,q;
struct Point
{
LL x,y;
Point(){}
Point(LL _x,LL _y):x(_x),y(_y){}
}points[MAXN],sta[MAXN],tmp[MAXN];
inline Point operator-(Point a,Point b)
{
return Point(a.x-b.x,a.y-b.y);
}
inline Point operator+(Point a,Point b)
{
return Point(a.x+b.x,a.y+b.y);
}
inline LL cross(Point a,Point b)
{
return a.x*b.y-a.y*b.x;
}
inline bool cmp(Point a,Point b)
{
if(a.x==b.x) return a.y<b.y;
return a.x<b.x;
}
int top=0,tot=0;
inline double Graham()
{
top=0;
sort(tmp+1,tmp+tot+1,cmp);
for(int i=1;i<=tot;i++)
{
while(top>=2&&cross(tmp[i]-sta[top-1],sta[top]-sta[top-1])>=0) top--;
sta[++top]=tmp[i];
}
int tmptop=top;
for(int i=tot-1;i>=1;i--)
{
while(top>=tmptop+1&&cross(tmp[i]-sta[top-1],sta[top]-sta[top-1])>=0) top--;
sta[++top]=tmp[i];
}
top--;
double sqr=0;
for(int i=1;i<=top;i++)
sqr+=(double)cross(sta[i],sta[i%top+1]);
return sqr/(double)2;
}
int main()
{
scanf("%d%d",&k,&n);
for(int i=1;i<=n;i++)
scanf("%lld%lld",&points[i].x,&points[i].y);
scanf("%d",&q);
while(q--)
{
LL a,b,c,d;
scanf("%lld%lld%lld%lld",&a,&b,&c,&d);
tot=0;
for(int i=1;i<=n;i++)
if(a<=points[i].x&&points[i].x<=b&&c<=points[i].y&&points[i].y<=d)
tmp[++tot]=points[i];
//cout<<Graham()<<endl;
printf("%.1lf\n",Graham());
}
return 0;
}
















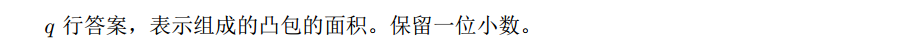
















 573
573

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








