红黑树 节点的删除

接上一篇。

红黑树的插入操作！

红黑树的删除继续分各种情况进行考虑。

首先考虑红黑树的单支情况，即只有父节点只有一个子节点，另外一个为NULL，这样的话，只有一种情况，即父节点为黑色，子节点为红色，因为其他情况都会是孩子为黑色，因为孩子为红色父为红色，则与红父黑子矛盾。而当孩子是黑色时，另一个孩子是黑色的NULL，则必定使左右路径上黑色节点数量不等。所以单支只能为黑父红子。

这里的单支情况，是对任意一点的，若其只有一个孩子，则其必为黑色，孩子必为红色，且孩子为叶子节点。孩子为红色，如果有孙子，其孙子必为黑色，则路径黑子数量不等，不平衡。

情况一：

单支，删除红色节点，则不会影响其他路径情况，不影响平衡，直接删除即可。

情况二：

单支，删除黑节点

若s节点为黑色，则用单支下的红色孩子替代自己，然后删除黑色节点，这样路径上少了一个黑色节点，影响平衡，需要进行调整。

情况三:

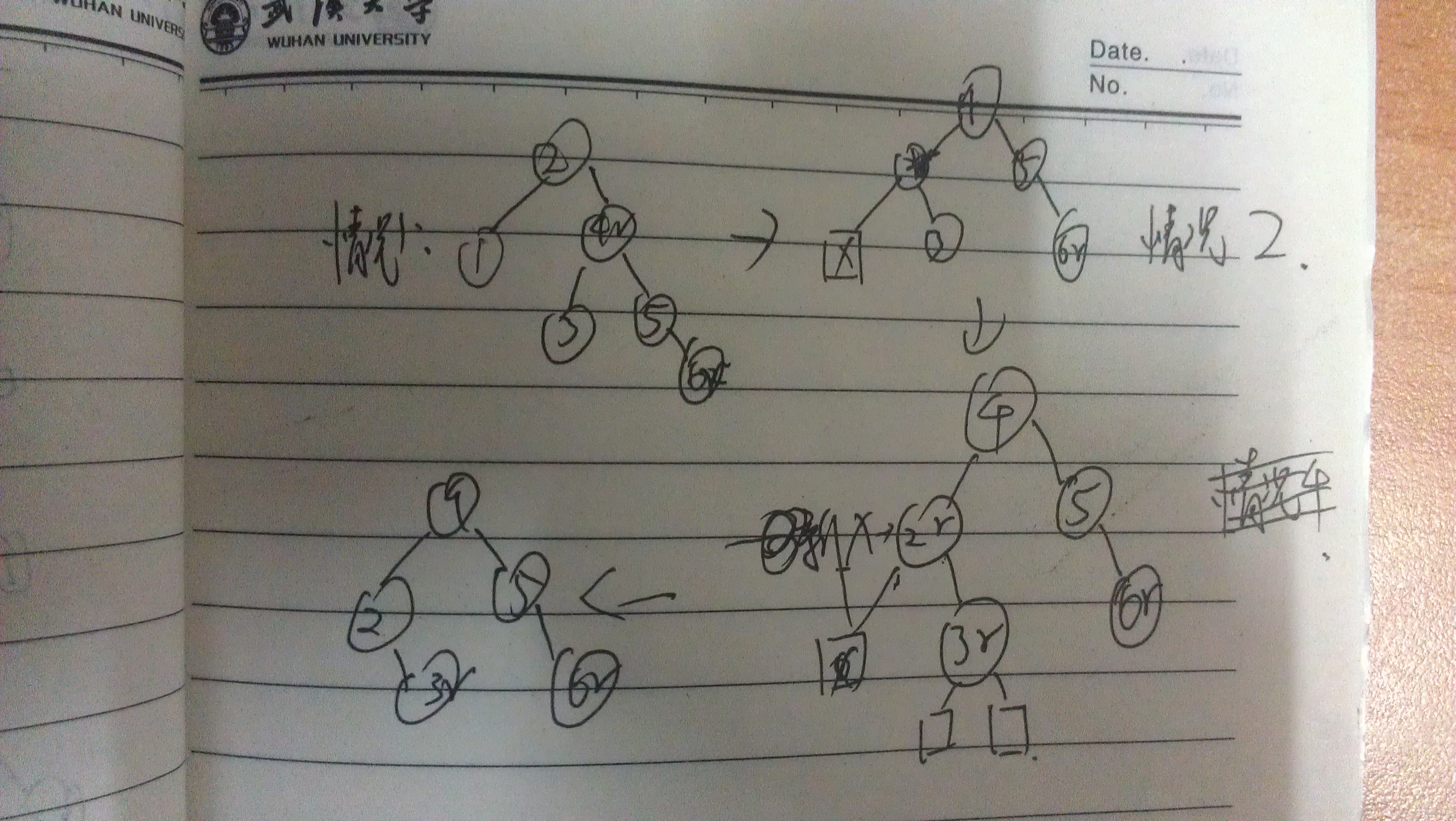
删除节点有两个非空孩子，这时候又用到向下旋转的思路，寻找删除节点p的中序遍历的后继节点s，即正常排序后位于p之后的数字，而且s节点必定最多有一颗子树，即s最多有一颗右子树，或者没有。若s节点有一颗右子树，则必为单支情况，其孩子为红色，且无孙子，则这就是情况二，转到情况二。若s节点为叶子节点，则其可为红色或黑色，红色为情况一。

这种情况将p与s的数据交换，但颜色不换，则情况转换为删除s点，而删除之前树还是平衡的。

或者这样分析：

若s节点为红色，则其必定不是单支，则其为叶子节点，则是情况一，直接删除即可。

若s节点为黑色，则用s的孩子null或者单支下的红色孩子替代自己，然后删除黑色节点，这样路径上少了一个黑色节点，影响平衡，需要进行调整。（这里又要注意，如果是孩子为NULL，替代后，如何找到s节点的父节点。没有哨兵节点，这个地方麻烦了。。。。好吧，调用的递归调整函数的参数加一个父节点指针）

然后如同插入一样设置一个递归的调整函数，调整有4种情况：

首先以删除判断节点为x，为黑色，父节点为p，兄弟节点为w。以x为根的子树的黑色节点树减一，则需要进行平衡操作。

一般是有一下4种情况，但，还有一个特殊情况，即x为根节点时，跟插入时判断相同，如果x为根节点，且现在为红色， 则将其改为黑色。对于以下情况2，可能转换到这种情况。第二次被别人的博客坑，等会写完了再测试有没有其他错误。

情况1：w为红色。

则w的孩子都为黑色，p为黑色。改变w和p的颜色，即w改为黑色，p改为红色，然后以p为支点进行左旋，或右旋，根据x位于p的位置决定，若x为左孩子，左旋，右孩子右旋。更新后x获得了新的兄弟节点，然后继续对x进行判断调节。

情况2：w为黑色，且w的孩子都为黑色。这里由于之前是在x所在子树上删除了一个黑色的节点，则w所在子树上必定有一个黑色节点，即w必定不为NULL。

将w置为红色，使w所在子树上黑色数量减一，则p所在子树上黑色节点数量也减一，则需要以p节点作为当前节点，即新的x节点。如果新的x为红，则将其置为黑色，则整个树平衡，结束，如果为黑，则继续判断新的x节点的情况。

情况3：w为黑色。

如果x为p的左孩子， w的左孩子为红色，右孩子为黑色。

则将w置为红色，左孩子为黑色，然后以w节点为支点右旋。

如果x为p的右孩子， w的右孩子为红色，左孩子为黑色、

则将w为红，右孩子为黑，然后以w节点左旋。

获得新的兄弟节点，进入情况4. 这里进行情况3的旋转不会对改变任何子树的平衡性。

情况4：w为黑色。

如果x为p的左孩子，w的右孩子为红色，左孩子可以为红色或黑色或NULL。

则交换w和p的颜色，因为之后w要成为新的父节点，所以要获得原来p的颜色，防止与p的父节点冲突。

将w的右孩子设置为黑色，这样w的右子树黑色节点树+1，

再以p节点为支点左旋，这样w的颜色黑色会移动到左子树，使其节点树 -1 + 1 =0，而右子树减少了一个黑节点 +1 -1 = 0；且新的p节点为原来的颜色，整个树是平衡的。结束、

如果x为p的右孩子，w的左孩子是红色。同理、

交换w和p的颜色，将w的做孩子改为黑色，以p为节点右旋。结束判断。

最终调整完成。这里也有一个很重要的地方，在左旋和右旋时交换父节点p与其对应左右孩子c的颜色，导致旋转后得到的新父节点p颜色未变，则不用再向上检测。

中间测试的时候有出错了，尝试画了一些图并找出了错误，只画了一张图，其他都是看别人的博客思考的。

删除其实也不是特别复杂，尝试写出代码：

template <typename T>
void RBTree<T>::GetParentLinked(RBNode<T> *a,RBNode<T> *b){
	if(a == root){
		root = b;
		if(b)
			b->parent = 0;
		return;
	}
	if(a->parent->left == a){
		a->parent->left = b;
		if(b)
			b->parent = a->parent;
	}else{
		a->parent->right = b;
		if(b)
			b->parent = a->parent;
	}

}
template <typename T>
bool RBTree<T>::Delete(const T &x){
	RBNode<T> *p = root ,*s,*fa;
	if(!root)return false;
	while(p){
		if(p->value == x)break;
		else if(x < p->value)p = p->left;
		else p = p->right;
	}
	if(p){
		if( p->left &&  p->right){//当存在左右孩子时，向下旋转
			s = p->right;
			while(s->left){
				s = s->left;
			}
			int temp = p->value;
			p->value = s->value;
			s->value = temp;
			p = s;
		}
		if(p->red){//为红色叶子节点，直接删除
			GetParentLinked(p,p->left);
			delete p;
		}else{//为黑色时，将其红色子孩子替代他
			//由于之前已经向下旋转，则这里只有一种特殊可能，即单支情况删除黑色根节点。			
			fa = p->parent;//之后可能没有父节点。
			if(p->left){
				s = p->left;
				GetParentLinked(p,p->left);				
			}
			else {
				s = p->right;
				GetParentLinked(p,p->right);
			}
			delete p;
			AdjustAfterDelete(s,fa);
		}
		return true;
	}else return false;

	
}
template <typename T>
void RBTree<T>::AdjustAfterDelete(RBNode<T> *x ,RBNode<T> *p){
	if(p){//如果有父指针，则有四种情况。
		RBNode<T> *w ;
		bool inLeftTree = true;//标记左右情况，左右情况不同旋转方向以及判断方式也不同。
		if(p->left == x)w = p->right;
		else {
			w = p->left;
			inLeftTree = false;
		}
		if(w->red){
			w->red = false;
			p->red = true;
			if(inLeftTree)
				LRotation(p);//以p为支点进行旋转，不用考虑当前节点是否为空。
			else
				RRotation(p);
			AdjustAfterDelete(x,p);
		}else{
			if( !GetColorWithNULL(w->left) && !GetColorWithNULL(w->right) ){
				w->red = true;
				x = p;
				if(x ->red)x->red = false;//出错一次，要根据新的x节点进行判断。
				else	AdjustAfterDelete(x,x->parent);
			}else if(( inLeftTree && GetColorWithNULL(w->right) ) //情况4
				|| ( !inLeftTree && GetColorWithNULL(w->left) )  ){
					bool tempRed = p->red;
					p->red = w->red;
					w->red = tempRed;
					if(inLeftTree){
						w->right->red = false;						
						LRotation(p);
					}else{
						w->left->red = false;
						RRotation(p);
					}
			}else {//情况3
				w->red = true;
				if(inLeftTree){
					w->left->red = false;
					RRotation(w);
					AdjustAfterDelete(x,p);
				}else{
					w->right->red = false;
					LRotation(w);
					AdjustAfterDelete(x,p);
				}
			}
		}
	}else{//如果不存在父节点，则此节点为根节点，则置为黑色结束。
		if(x)
			x->red = false;
		return ;
	}

}

我的红黑树代码！