贷款买房问题的决策分析研究

系统简介

近些年来，由于房地产经济的持续火热，人们对贷款买房也充满了关注。商业性的贷款方式和公积金的贷款方式是目前比较重要的贷款方式。等额本金的还贷方式和等额本息的还贷方式也是目前比较时兴的还贷方式。本文首先是在贷款买房问题和还款问题的分析的基础上，对月还款额、总利息等进行一个递推，运用迭代法，建立一个购房还款模型，对贷款买房问题给予一定程度的决策分析，使工薪阶层的人士买房这个梦想更加合理快捷地变成现实。并且结合一个具体的实例进行求解得出最优方案。最后依据所建数学模型进行数据剖析，对贷款买房的问题进一步探讨。
关键词 还款模型 迭代法 决策分析 数据分析

1.绪论

1.1论文研究的背景
由于购买商品房已经成为近些年来的热点问题，使得许多工薪阶层的人士也参与其中。从目前所收集到的数据来看，大多数工薪阶层人士会倾向于选择贷款买房，是因为这些年来房价涨幅较快，多数人难以一次性支付全部房款，通过对贷款买房问题的决策性分析，这样可以解决无法一次性付清房款的问题。
假设某个工薪阶层人士，在某地预买一间住房，因为手头不够富裕，他会选择贷款买房，贷款多久才最划算，选择什么贷款方式和还贷方式最便利，这些都是现在的工薪阶层人士最想知道答案的问题。所以在我们考虑贷款而去银行前，就一定要对贷款方式和还款方式有一些了解，同时也要依据自身的经济情况采取最佳方案完成贷款和买房。目前，在社会上热度最高的还款方式是等额本息贷款和等额本金贷款，两者皆各有其优劣，所以需要进一步的决策分析。
存贷款利率由中国人民银行统一发布，如图 1、图 2所示：

图 1商业住房贷款基准利率

图 2公积金的贷款方式的利率
1.2贷款介绍
1.2.1按揭贷款
在目前高速发展的社会大背景下，对于一些家庭经济状况有富余的买房者，他们面对日渐高昂的房价也没有足够的底气拿出全款买房，若他们一定要等到钱凑够了再买房，在这期间房价也会有一定的增长，这个过程可能比较漫长，同时也需要接受在攒钱期间可能会产生的意外情况等等。若他们选择贷款买房的方式，虽然每个月需要清偿一些钱款，但是这些资金的运转对家庭生活本身是没有影响的，与此同时，买房者还可以住进新房。
当然，这种贷款方式不只对买房者有好处，它对房屋的开发公司和银行的好处都是非常大的，对整个国家的市场都是有一定影响的。按揭贷款从银行的角度而言，若银行对房屋的开发公司提供贷款业务，房屋的开发公司可以用这笔贷款建房，但是卖房会有一定的流程，会耗费比较长的时间。因此会对房屋的开发公司还银行的贷款有一些影响。若银行对买房者提供贷款业务，买房者本身也还是要给一些钱款，因为银行提供的贷款数一般比需要买房的少，但因为买房者将房屋当作抵押给了银行，这提高了清偿贷款的信誉度；且对房屋的开发公司的整体资金的流通有很大的益处。
按揭贷款的含义是指买房者在接受贷款前已付清首付款，并且将用所贷资金买的房屋给银行当作抵押以此来保证可清偿余下金额的贷款形式。按揭贷款包括两种不同方面的意义，分别是房屋的抵押和划分不同期限归还钱款。它是指买房者将财产的产权转让于银行作为归还钱款的保证，在还清钱款后，买房者才可以得到房屋的产权。买房者依据与银行的合同中的规定按时还贷，银行可以依据相应的的利率获得利息。如果买房者不按时还贷，银行可以随时收回房屋。
1.2.2公积金贷款
公积金贷款的含义是指员工和他的单位定时上交的公积金被公积金的管理办公室交给银行使用，银行会将公积金提供给上交公积金的员工用来买房服务。到现在为止，公积金有几种重要的形式，分别是商品房屋的贷款形式、二手房屋的贷款形式等等。
应用公积金贷款需要满足的要求包括以下几点：（1）买房者的经济状况证明其有及时还贷的能力并且其本身的信誉较好；（2）买房者要提供可证明其身份的材料；（3）买房者要正常交存公积金大于或者等于一年；（4）买房者本身和他的丈夫（妻子）要确保他们没有其余的公积金贷款需要偿还；（5）买房者要将此公积金贷款买的房屋给银行当作抵押且要提交相应的保证材料；（6）在接受公积金贷款前要结清所买房屋的首付款。
1.2.3商业性贷款
商业性的贷款方式的本质是指当买房者在城市买房或是建立住房时，银行的信贷资金所提供的贷款服务。买房者将所贷的资金用来买的房屋给银行当作抵押，以此来证明自己可以清偿贷款。
应用商业性贷款需要满足的要求包括以下几点：（1）买房者的经济状况证明其有及时还贷的能力并且其本身没有失信行为；（2）买房者要提供可证明其身份的材料；（3）买房者要和房屋的开发公司订立正当的协议；（4）年纪对可贷的时间有一定的影响，买房者的年纪要超过18周岁且低于65周岁；（6）在接受商业性贷款前要结清所买房屋的首付款。
1.2.4.公积金贷款和商业性贷款的区别
（1）获取贷款的渠道不一样。员工和其工作单位正常交存的住房公积金是公积金贷款方式获取贷款的渠道；商业性质银行的人民或者单位的存款是商业性贷款方式获取贷款的渠道。
（2）对应的贷款人不一样。交存公积金大于等于一年，且保持固定的经济情况，有能力进行还款的就可以进行公积金贷款；有能对自身负责并有安稳经济情况的居民，都可以进行商业性贷款。
（3）两者的年利率不一样。二者对比下，公积金贷款方式的年利率要比商业性贷款方式的年利率低，并且当所贷的时间变长，二者需还的钱款会差距更大。
（4）两者前期的花费不一样。商业性的贷款方式在前期需要投入保险用费、律师的用费等。
（5）二者的可贷数额不一样。公积金的交存状况、房屋价格的成数、可贷的最大额数和买房者的还贷能力中的最小值就是公积金贷款方式的可贷数额。有公式：买房者的还贷能力：每个月需还的钱款+买房者负担的其余欠款+1230×2<家庭经济可承担的度。
房屋价格的成数、买房者的还贷能力两个因素其中相对小的就是商业性贷款的额度，有公式：买房者的还贷能力：（每个月需还的钱款+买房者负担的其余欠款+物业费）×2<家庭经济可承担的度。
（6）两者在贷款中的程序不一样。商业性贷款的程序是买房者签好合同文件后就可以到银行享受贷款业务。公积金贷款的程序会首先要去管理公积金的地方进行申请，若通过才可享受银行的贷款业务。因此公积金贷款的程序繁琐且耗费时间长。
1.3等额本息还贷法和等额本金还贷法的介绍
等额本息的还贷方式是不同于等额本金还贷方式的清偿贷款的计算方式。它们的本质是相同的：每个月开始余下的本金×当月的利率（年利率÷12）＝每个月需支付的利息。所不同的是等额本金前期每月的还款额比等额本息要多，多的部分就是所还的贷款本金。
等额本息还款法是指一种清偿所贷钱款的还款方法，买房者在还款期内，每个月归还相等额数的息金，其中本金根据买房者的借款时期（月）通过计算分配到每月，买房者按月还清。每个月所还的本金和利息的金额不相同，但所还的本金加要付的利息总额相同。随着贷款余下本金额的不断减少每个月所付的贷款利息额在递减，每个月所还的贷款本金额在增加。
等额本金的还贷方式的本质就是在与银行签订的截止日期前将所贷的钱款的本金部分按月均分，之后按月还的本金数是固定的，利息数是依据减去前一个月已经归还的钱款后剩余本金部分产生的。这样的还贷方式会导致月份增加后，需还的钱款却变少的情况。
1.4迭代法的介绍
迭代法的另一个名字是辗转法，是使用可变量之前的值不断的类推出新的值的过程。迭代的算法方式是一类比较基本的计算方法，尤其是在利用计算机来计算数值时应用最为广泛。因为计算机本身比较擅长相似性的计算，在使用可变量之前的值不断的类推出新的值的过程中，计算机依然可以保持非常迅速。
迭代的算法方式是一种利用类推公式或者循环性算法通过构造序列来求问题近似值的方法。例如，对于非线性方程，利用类推关系式，从开始按次序计算，来贴近方程的根值的方法，若只与有关，即，则称此迭代法为单步迭代法；对于线性方程组，由关系式从开始依次计算来贴近方程的解的方法。若对某一正整数，当时，与没有关系，该迭代的算法方式通常被称为定常迭代的算法方式，序列被称为迭代的序列。
迭代的算法方式使用的三个步骤如下：第一步就是找到算法方式中的可变量。在使用可变量之前的值不断的类推出新的值的过程前，要最少找到一个变量。第二步是构造出关于变量的相应迭代式。这个迭代式就是使用可变量之前的值不断的类推出新的值的过程。迭代的算法方式中最重要的一步就是构造相应迭代式，一般会按顺序一步步往后推得或者从结果往前推得。第三步是指要把握迭代的算法方式的整体进程。这种把握整体进程有两种情况，要么迭代的次数一定且易算，要么迭代的次数不一定。对于迭代的次数一定时，把握整体进程的方法就要建立确定次数的循环；对于迭代的次数不一定时，把握整体进程的方法就要继续深究怎么将整体进程终止。

2.模型建立

2.1模型假设和符号说明
2.1.1模型假设
(1)假设此工薪阶层人士在规定的贷款时间内经济情况正常。
(2)银行在贷款期限内月利率不变。
(3)每个月的月末贷款人将还款额付给银行。
(4)银行使用复利计算的方法来计息。
2.1.2符号说明
表 1符号说明表
符号 符号说明
需向银行贷款本金；
在第月还款后,仍欠银行的本息；
第月的还款额；
第月的利息；
贷款月利率；
还款总利息；
总还款期限。

2.4等额本金还款
根据等额本金贷款的定义所知，等额本金还贷方法是指先清偿本金然后再清偿利息，所以首先要将还款的总期限按月划分为时间段，其中每个时间段中还款本金是相同的，同时，还款利息会随着时间段发生变化而递减，从而得出等额本金贷款的模型。采用数学归纳法证明。
由等额本金还贷法的定义可知，第一个月，贷款本金，先还本金的部分为，然后再加上利息的部分为，则第一个月需归还的还款额为。
第二个月，每月需还本金相同为，此时的利息部分为，则第二个月需归还的还款额为。
第三个月，每月需还本金依然为，此时由利率可得的利息为，则可以得知第三个月需归还的还款额为。
使用递推法，以此类推……
最终得到第个月需归还银行的还款额为：
（10）

所需还款利息总额为：
（11）

由此可知,第一个月还款的额数最大,随着时间的递增,还款额数将会减少。

3.具体实例分析

本章我们将运用几个具体实例来对前面所讲述的贷款买房策略做实际分析，这对直观地认识贷款买房不同策略。

3.1引例
例：林先生是一名工薪阶层人士，收入稳定，2020年前计划买一套商品房作为婚房，婚房面积是115平米，他选择公积金贷款方式贷款了60万，还贷的期限为15年，利率为3.25%，林先生每个月的收入为7000元，我们可以分别使用等额本金法和等额本息法对此案例进行分析。在以上背景条件下，林先生每月的还款额数以及总利息是多少，并由此对林先生应该使用等额本息还贷法还是等额本金还贷法去还贷进行决策。
解：等额本息还贷法每一个月需还贷的金额数：

等额本息总利息：

等额本金还贷法每一个月需还贷的金额数：
第一个月:

第二个月:

第三个月：

最后一个月：

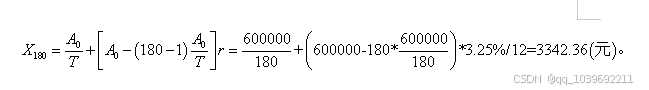
等额本金总利息：

答：在已知条件背景下，林先生使用等额本息的还贷方式时每个月的需还4216.01元，利息总和158882.27元；使用等额本金的还贷方式时最初的一个月需还4958.33元，第二个月需要还4949.31元，最后一个月需要的还3342.36元，利息总和是147062.5元。由于林先生收入的30%要留下以供日常开销，残余金额为4900元，故虽然等额本金还贷法的利息数比等额本息法还贷时利息数要少一些，然而基于林先生的详细经济情况，还是应选择等额本息还贷法。
3.2问题举例
例：曹女士在宿迁市预备买一套商品房，其经济条件稳定，该商品房价值120万元，首付为房价的30%，这是曹女士的第二套房，曹女士一家每一个月总的收入为12000元，剩余房款可选择采用公积金贷款或商业性贷款进行贷款。现有四个贷款方案可供曹女士来选择，如下：
方案一：贷10年期，84万元，公积金的贷款方式，等额本息的还贷方式。
方案二：贷12年期，84万元，公积金的贷款方式，等额本金的还贷方式。
方案三：贷9年期， 78万元，商业性的贷款方式，等额本息的还贷方式。
方案四：贷11年期，78万元，商业性的贷款方式，等额本金的还贷方式。
对这四种方案进行分析，帮助曹女士得出贷款买房的最优方案。
解：方案一：当选择采用公积金贷款方式时，可贷10年的期限，则年利率是3.25%。应用等额本息的还贷方式时需还的利息为：

方案二：当选择采用公积金贷款方式时，可贷12年的期限，则年利率是3.25%。使用等额本金的还贷方式所需还的利息为：

方案三： 当选择采用商业性贷款时，可贷9年的期限，则年利率是4.9%。应用等额本息的还贷方式所需还的利息为：

方案四：当选择采用商业性贷款方式时，可贷11年的期限，则年利率是4.9%，使用等额本金的还贷方式所需还的利息为：

答：经过以上对四个方案的总利息的计算，由方案一可知每月需要还8208.4元，利息总和为145007.81元；方案二中最初的一个月需要还8108.33元，利息总和为164937.5元；方案三每月需要还8945.89元，利息总和为186156.41元；方案四最初的一个月需要还为9094.09元，利息总和为211802.5元。由题目可知，曹女士一家每一个月总的收入为12000元，则他们可支配用来还贷的资金为8400元，因此，结合还款额和总利息的数据对比，曹女士一家应选择方案一进行还款。

4.数据对比分析

4.1等额本息时数据对比分析
当还贷方式为等额本息还贷法时，由于贷款金额主要是由贷款者的实际情况决定的，不具备统一讨论的意义，故可将贷款金额固定来进行数据分析。且由实际情况可知，贷款买房最多可贷30年。
表 2等额本息还款计算对比
年份(年） 贷款金额（元） 公积金贷款利率 公积金贷款每月还款额（元） 公积金贷款总利息（元） 商业性贷款利率 商业性贷款每月还款额（元） 商业性贷款总利息（元）
0.5 200000 2.75% 33,601.20 1607.23 4.35% 33,757.53 2545.15
1 200000 2.75% 16,915.97 2991.67 4.35% 17,061.98 4743.76
2 200000 2.75% 8,574.14 5779.44 4.75% 8,751.90 10045.67
3 200000 2.75% 5,794.23 8592.37 4.75% 5,971.76 14983.23
4 200000 2.75% 4,404.80 11430.47 4.75% 4,583.24 19995.69
5 200000 2.75% 3,571.56 14293.72 4.75% 3,751.38 25082.94
6 200000 3.25% 3,061.16 20403.2 4.90% 3,211.72 31243.66
7 200000 3.25% 2,665.25 23881.41 4.90% 2,817.39 36661.07
8 200000 3.25% 2,368.69 27394.59 4.90% 2,522.47 42157.41
9 200000 3.25% 2,138.36 30942.7 4.90% 2,293.82 47732.41
10 200000 3.25% 1,954.38 34525.67 4.90% 2,111.55 53385.75
11 200000 3.25% 1,804.12 38143.43 4.90% 1,963.01 59117.07
12 200000 3.25% 1,679.14 41795.91 4.90% 1,839.76 64925.99
13 200000 3.25% 1,573.61 45483.02 4.90% 1,735.97 70812.08
14 200000 3.25% 1,483.36 49204.66 4.90% 1,647.47 76774.89
15 200000 3.25% 1,405.34 52960.76 4.90% 1,571.19 82813.92

年份(年） 贷款金额（元） 公积金贷款利率 公积金贷款每月还款额（元） 公积金贷款总利息（元） 商业性贷款利率 商业性贷款每月还款额（元） 商业性贷款总利息（元）
16 200000 3.25% 1,337.25 56751.19 4.90% 1,504.84 88928.66
17 200000 3.25% 1,277.33 60575.84 4.90% 1,446.66 95118.55
18 200000 3.25% 1,224.23 64434.61 4.90% 1,395.29 101383
19 200000 3.25% 1,176.87 68327.36 4.90% 1,349.66 107721.42
20 200000 3.25% 1,134.39 72253.97 4.90% 1,308.89 114133.14
21 200000 3.25% 1,096.09 76214.28 4.90% 1,272.29 120617.52
22 200000 3.25% 1,061.39 80208.17 4.90% 1,239.29 127173.84
23 200000 3.25% 1,029.84 84235.48 4.90% 1,209.43 133801.39
24 200000 3.25% 1,001.03 88296.06 4.90% 1,182.29 140499.42
25 200000 3.25% 974.63 92389.74 4.90% 1,157.56 147267.17
26 200000 3.25% 950.37 96516.34 4.90% 1,134.95 154103.84
27 200000 3.25% 928.01 100675.71 4.90% 1,114.22 161008.62
28 200000 3.25% 907.34 104867.66 4.90% 1,095.18 167980.69
29 200000 3.25% 888.20 109092 4.90% 1,077.64 175019.18
30 200000 3.25% 870.41 113348.55 4.90% 1,061.45 182123.24
由表 2可知，在还贷的方式是等额本息还贷方式的前提下，贷款的总金额一定时，随着贷款年限的增加和贷款方式的不同，贷款基准利率会产生相应的增长，这使得最后需要还付的利息也产生相应的增加，可以看到在还款期限增加的过程中，总利息增长区间较大，但每月还款金额会相对减少。从数据可以大致分析出来，贷款1年时，每月还款额较大，总利息较少；贷款15年时，每月还款额较少，总利息较多；贷款5年时，每月还款额适中，总利息也适中。

图 3等额本息还款每月还款额及总利息变化
由图 3可以看出在等额本息还贷方式的前提下公积金贷款方式与商业性贷款方式的趋势对比，总的来说，商业性贷款方式下每月的还贷额数和利息总和数都比公积金贷款方式下每月还贷额数和利息总和数要多，公积金贷款方式的增长趋势相对于商业性贷款方式要缓慢一些，商业性贷款涨幅较大。此外，可以看出当使用商业性贷款时的贷款期限是4年期最为划算，但是使用公积金贷款方式的贷款期限为5年期时最划算。
4.2等额本金时数据对比分析
当还贷的方式为等额本金还贷法时，每个月需要还的本金数是相同的，每月需要还的利息会有所改变，同样可以固定贷款金额为200000元进行数据分析。
表 3等额本金还款计算对比
年份(年） 公积金贷款利率 第1个月还款额（元） 第2个月还款额（元） 最后一个月还款额（元） 等额本金公积金贷款总利息（元） 商业性贷款利率 等额本金商业性贷款总利息
0.5 2.75% 33,791.67 33,715.28 33,409.72 1604.17 4.35% 2537.5
1 2.75% 17,125.00 17,086.81 16,704.86 2979.17 4.35% 4712.5
2 2.75% 8,791.67 8,772.57 8,352.43 5729.17 4.75% 9895.83
3 2.75% 6,013.89 6,001.16 5,568.29 6013.89 4.75% 14645.83
4 2.75% 4,625.00 4,615.45 4,176.22 11229.17 4.75% 19395.83
5 2.75% 3,791.67 3,784.03 3,340.97 13979.17 4.75% 24145.83

年份(年） 公积金贷款利率 第1个月还款额（元） 第2个月还款额（元） 最后一个月还款额（元） 等额本金公积金贷款总利息（元） 商业性贷款利率 等额本金商业性贷款总利息
6 3.25% 3,319.44 3,311.92 2,785.30 19770.83 4.90% 29808.33
7 3.25% 2,922.62 2,916.17 2,387.40 23020.83 4.90% 34708.33
8 3.25% 2,625.00 2,619.36 2,088.98 26270.83 4.90% 39608.33
9 3.25% 2,393.52 2,388.50 1,856.87 29520.83 4.90% 44508.33
10 3.25% 2,208.33 2,203.82 1,671.18 32770.83 4.90% 49408.33
11 3.25% 2,056.82 2,052.71 1,519.26 36020.83 4.90% 54308.33
12 3.25% 1,930.56 1,926.79 1,392.65 39270.83 4.90% 59208.33
13 3.25% 1,823.72 1,820.25 1,285.52 42520.83 4.90% 64108.33
14 3.25% 1,732.14 1,728.92 1,193.70 45770.83 4.90% 69008.33
15 3.25% 1,652.78 1,649.77 1,114.12 49020.83 4.90% 73908.33
16 3.25% 1,583.33 1,580.51 1,044.49 52270.83 4.90% 78808.33
17 3.25% 1,522.06 1,519.40 983.05 55520.83 4.90% 83708.33
18 3.25% 1,467.59 1,465.08 928.43 58770.83 4.90% 88608.33
19 3.25% 1,418.86 1,416.48 879.57 62020.83 4.90% 93508.33
20 3.25% 1,375.00 1,372.74 835.59 65270.83 4.90% 98408.33
21 3.25% 1,335.32 1,333.17 795.80 68520.83 4.90% 103308.33
22 3.25% 1,299.24 1,297.19 759.63 71770.83 4.90% 108208.33
23 3.25% 1,266.30 1,264.34 726.60 75020.83 4.90% 113108.33
24 3.25% 1,236.11 1,234.23 696.33 78270.83 4.90% 118008.33
25 3.25% 1,208.33 1,206.53 668.47 81520.83 4.90% 122908.33
26 3.25% 1,182.69 1,180.96 642.76 84770.83 4.90% 127808.33
27 3.25% 1,158.95 1,157.28 618.96 88020.83 4.90% 132708.33
28 3.25% 1,136.90 1,135.29 596.85 91270.83 4.90% 137608.33
29 3.25% 1,116.38 1,114.82 576.27 94520.83 4.90% 142508.33
30 3.25% 1,097.22 1,095.72 557.06 97770.83 4.90% 147408.33
由表 3可知，在等额本金的还贷方式的前提下，每个月需要的还款额数都会减少，且减少的金额在随着贷款期限的增加而增加，成正比。在同一期限下，等额本金还贷方式的月还贷额数会每个月减少同样的金额。商业性贷款方式的利息总和和每个月的还贷额数都比公积金贷款方式的要多一些。在贷款期限的增加过程中，商业性贷款的总利息也比公积金贷款的总利息要多。

图 4等额本息方式和等额本金方式下总利息的对比
由图 4可以看出等额本息方式和等额本金方式下总利息的对比，随着贷款期限的增加，等额本金下的总利息和总额本息下的总利息变化都呈现上升趋势，且可以发现商业性贷款无论是在等额本息还款下还是等额本金还款下的总利息变化都比公积金贷款的总利息趋势更加陡峭，所以商业性贷款总利息要比公积金贷款总利息要多。

图 5月还贷额比较

由图 5可知等额本金的还贷方式在开始的一个区间内的月还贷额会比等额本息还贷方式的月还贷额高一些，开始时需要还6297.5元，最后需要还3677.6元，逐月递减10.96元。但是到了第106个月的点时，两者会产生交汇，接下来等额本息还款的月还款额将会比等额本金的月还款额高。

结论

5.1模型结论
通过对所提出的问题的研究探讨和数据分析，我们首先了解到贷款利率、贷款本金、还款期限和贷款方式等因素都对最后得出的月还款额和总利息产生较大的影响，贷款利率是通过改变贷款方式及贷款年限而产生不同的，使用等额本金还款和使用等额本息还款的月还款额和总利息也随着还款期限等因素的变化而不同。其次从实际生活的角度出发，选择贷款的具体方式不仅仅因为银行的基准利率、贷款限制的时间等因素的影响,它最终还是由买房者的经济详细状况来决定。
在现实生活中来看，等额本金还款法与等额本息还款法二者之间没有非常明确的关于好或坏的划分，尽管等额本息还款法比等额本金还款法的需还款金额数相对少一些，然而主要都是依据不同买房者本身的收入详细状况来决定的。等额本息还款法的好处就在于它能够使之后的规划和还款更加便利，并且它的每个月的还款额数是相同的，对于本金与利息之间的清偿比重来说，在前一段时间里需还的本金比利息要少，当规定的还贷期限超过一个临界点后需要还的本金就比利息要多。同时可以得出结论，等额本金的还贷方式相较于等额本息的还贷方式需要清偿的的总利息数要少一些，并且当贷款的时间越久，总利息数额间的差数就会越来越多。然而由于等额本息的还贷方式的每个月还贷额数是相同的，对于工薪阶层家庭日常支出的估计是有利的，尤其是青年人，适合采用等额本息还款法，并依据自己的具体收入来选择合适的还款期限,因为有可能随着年龄增长或者职位高升，经济收入会有一定的增加。
等额本金还贷方式在每一个月的还贷额数都是不一样的，详细来说就是本金的总额数会依据还贷规定的月份数进行均分，与上一个月残余本金所产生的利息相加，从而得到这个月的还贷总额数。因此等额本金的还贷方式最开始的时候需要还的金额是最大的，随着还贷月数的递增，后面需要还贷的金额就会变少。一些年纪偏大的买房者可以考虑使用这种还贷方式进行还贷，主要的原因就是等额本金这种还贷方式在贷款的前一时期还款总额数还是比较高的，年纪偏大的买房者后期可能会经历退休等变动，还贷能力有可能会下降。如果有些人的收入状况比较乐观，希望前期就可以多还一些，减少后面的还贷压力，也可以考虑这种还贷方式。如果买房者对自己的收入没有自信,觉得自己的收入不够稳定,那么可以适量的延长一点还款期限,虽然这样的选择会使需偿还的利息数增大,但是在较长的时间里,该买房者可以有更多的机会进行投资,如果买房者投资所获得的收益大于需还给银行的利息数,那么这样的选择也是可行的。
5.2模型改进
通过对上文模型的思考理解，我们主要是从还款方式出发，来对具体应用进行分析决策，但贷款买房方面的问题还有很多可以深究的地方，比如对贷款的风险估测，还可以从贷款方式作为突破口来深入考虑，所以本模型还具有很大的改良空间，以后能够在这些方面继续做更多的探究。
另一方面，由于本篇文章只研究了工薪阶层人士选择公积金贷款方式或者商业性贷款方式进行贷款，但是在现实生活中，人们还可以选择组合贷款的方式，即选择一些使用公积金贷款的方式，另外一些选择使用商业性贷款的方式。并且在使用商业性贷款的方式中有的银行可能会提供一些折扣，这些都要根据实际情况决定的。