最近要学习R-CNNs,参考的论文是< Rich feature hierarchies for accurate object detection and semantic segmentation > 。首先的步骤就是selective search。所以先学习下。
Exhaustive Search
选择一个窗口(window)扫描整张图像(image),改变窗口的大小,继续扫描整张图像。显然这种做法是比较“原始的”,改变窗口大小,扫描整张图像。这种做法很费时。因此,J.R.R. Uijlings发表的2012 IJCV介绍了选择性搜索的算法。
Selective Search
Part 1 Efficient Graph-Based Image Segmentation
首先介绍使用的一种分割算法,这个算法是2004年由Felzenszwalb发表在IJCV上的。主要介绍了基于贪心选择的图像分割,这种方法能考虑到全局特征。
We then develop an efficient segmentation algorithm based on this predicate,and show that although this algorithm makes greedy decisions it produces segmentations that satisfy global properties.
对于一个分割算法,要想得到broad utility,应该能提取出重要区域并且能高效的运行。就像Urquhart 1982 所用的方法类似,文章的算法基于用图表示图像:图像中的每个像素表示图上的一个节点,每一条连接节点的无向边都具有一个权重(weights),以衡量其连接的两个节点之间的不相似度(dissimilarity)。与传统方法不同的是,本文会根据相邻区域在特征值上变化速度的大小动态调整分割阈值(Adaptively adjusts the segmentation criterion based on the degree of variability in neighboring regions of the image)。

上图这个例子说明,图像分割算法既不能单一的使用像素强度值的变化作为分割依据,也不能使用单一的分割阈值来决定分割与否。所以文章中提到的算法基于两个特征来判断两个区域是否应该合并:
区域间间距和区域内间距。
如果两个区域的区域间间距明显大于其中任意一个区域的区域内间距,那么就认为这两个区域之间存在明显的界限(即不可以merge两个区域)。
Pairwise region comparison predicate 区域对比较断言


1)定义了区域内间距
即区域对应MST(minimum spanning tree最小生成树)中权重最大的边的权重值。
2)定义了区域间间距
即在所有分别属于两个区域且有边连接的点对中,寻找权重最小的那对(若两个区域内的点没有边相连,则定义间距为正无穷大)。
有了区域内间距和区域间间距的定义之后,通过比较两者之间的关系,就可以得出断言函数的形式:


注意,此处的τ是一个阈值函数,用来控制两个区域的区域间间距要在多大程度上大于他们的区域内间距才能被认定为两个区域间有明显的分割界限。
举个例子来说,当其中一个区域很小时,Int(C)并不能很好的反应其区域内间距(极端的情况是当C只含一个节点时,Int(C)=0)
本文在此处对τ的定义为|C|的负相关函数:

其中k是一个常数。k要根据实验的具体情况来确定其值,但当k越大时,我们界定的可以区分两个区域的界限就越明显。更重要的是,只要不与实验目的相悖,任何非负函数都可以用来表示τ。比如:如果我们需要将图像分割成为特定形状的区域,则可以将τ定义为与复合这个特定形状正相关的函数。而且τ对特定形状的倾向性可强可弱。这确保了开头提到的第一条性质的实现。
segmentation 分割算法
输入是一个有n个节点和m条边的图G,输出是一系列区域。步骤如下:
0.将边按照权重值以非递减方式排序
1.最初的分割记为S(0),即每一个节点属于一个区域
2.按照以下的方式由S(q-1)构造S(q):记第q条边连接的两个节点为vi和vj,如果在S(q-1)中vi和vj是分别属于两个区域并且第q条边的权重小于两个区域的区域内间距,则合并两个区域。否则令S(q) = S(q-1)。
3.从q=1到q=m,重复步骤2
4.返回S(m)即为所求分割区域集合
算法过程保证了开头提到的第二条性质。
接下来论文具体实现了两种算法:基于Grid Graphs的和基于Nearest Neighber Graphs的方法。
两者的区别在于graph中节点和边的选取方式的不同:GG方法将图像中的每个元素视为一个节点,只要两个像素相邻,则认为其对应的节点之间有边连接(一般来说,每个节点有8条边)。边的权重值为对应两个节点的像素值差值的绝对值。(细节方面,1预处理过程使用σ=0.8的高斯函数来对图像进行平滑以减少噪声。2当图像为三通道图像时,将算法应用于全部三个通道,只有当三个通道全部给出合并区域的建议时才合并区域。3文章中使用的k值,当图片是128*128时k=150,当图片是320*240时k=300,即k值大概与图片尺寸成正比)。NNG方法先将图像的每个像素映射到特征空间形成图的节点,然后利用特征空间中的距离选取与其距离最近的点作为他们的邻居(有多种方法来选择邻居节点,即可以选择与其最近的k个邻居点,也可以选择与其距离不超过d的所有点作为邻居点),连接邻居点的边权重为两个对应节点在特征空间内的距离。
结果说明,NNG算法比GG算法在保证算法第一条性质的效果上要更好一些。
part 2 Hierarchical Grouping Algorithm

我们首先用上述分割算法得到一些初始化的区域R={r1,….rn}
计算出每个相邻区域的相似性s(ri,rj)
1. 找出相似性最大的区域max(S)={ri,rj}
2. 合并rt=ri∪rj
3. 从S集合中,移走所有与ri,rj相关的数据
4. 计算新集合rt与所有与它相邻区域的相似性s(rt,r*)
5. R=R∪rt
直到S集合为空,重复1~5。
Scolor(ri,rj)用于计算ri,rj的相似性。对每个区域,我们都可以得到一个一维的颜色分布直方图。直方图一共有25个区间,区域i的颜色分布直方图为
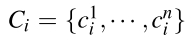
如果有3个颜色通道,则n=75。还要用L1 norm来进行归一化。
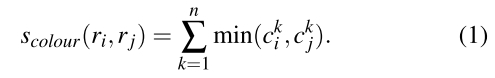
当i和j合并成t,区域t的颜色分布直方图可以用下面式子进行计算:
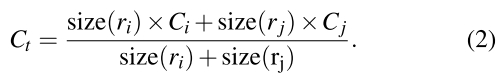
t 的size用下面式子计算:
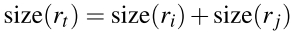
Stexture(ri,rj)我们可以用到SIFT(局部特征描述子)
我们取8个方向,方差为1的高斯滤波器,10个空间的直方图来描述。
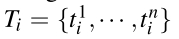
如果有3个颜色通道,n=240=8*3*10,同理得到区域i的纹理直方图要用L1norm归一化。
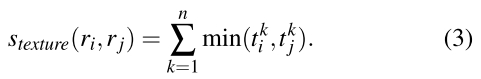
同理,纹理的传递性也可以用(2)式解决。
Ssize (ri,rj)鼓励小的区域尽早合并。
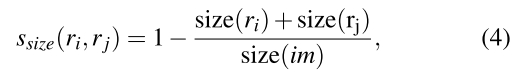
size(im)表示整个图片的像素数目。
Sfill (ri,rj)鼓励有相交或者有包含关系的区域先合并。
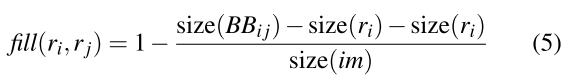
BBij指包含i,j区域的最小外包区域。
在这篇文章中,我们用到如下计算相似性:








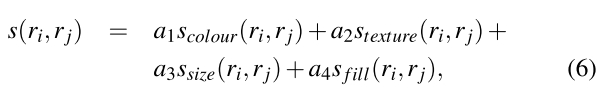














 1362
1362

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








