LeetCode 100道题目和答案（面试必备）（三）

75.跳跃游戏

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

答案

方法一：贪心
我们可以用贪心的方法解决这个问题。

设想一下，对于数组中的任意一个位置 y，我们如何判断它是否可以到达？根据题目的描述，只要存在一个位置 x，它本身可以到达，并且它跳跃的最大长度为 x+nums[x]，这个值大于等于 y，即 x+nums[x]≥y，那么位置 y 也可以到达。

换句话说，对于每一个可以到达的位置 x，它使得 x+1,x+2,⋯,x+nums[x] 这些连续的位置都可以到达。

这样以来，我们依次遍历数组中的每一个位置，并实时维护 最远可以到达的位置。对于当前遍历到的位置 x，如果它在 最远可以到达的位置 的范围内，那么我们就可以从起点通过若干次跳跃到达该位置，因此我们可以用 x+nums[x] 更新 最远可以到达的位置。

在遍历的过程中，如果 最远可以到达的位置 大于等于数组中的最后一个位置，那就说明最后一个位置可达，我们就可以直接返回 True 作为答案。反之，如果在遍历结束后，最后一个位置仍然不可达，我们就返回 False 作为答案。
public class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;
        int rightmost = 0;
        for (int i = 0; i < n; ++i) {
            if (i <= rightmost) {
                rightmost = Math.max(rightmost, i + nums[i]);
                if (rightmost >= n - 1) {
                    return true;
                }
            }
        }
        return false;
    }
}

76.跳跃游戏II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

方法一：反向查找出发位置
我们的目标是到达数组的最后一个位置，因此我们可以考虑最后一步跳跃前所在的位置，该位置通过跳跃能够到达最后一个位置。

如果有多个位置通过跳跃都能够到达最后一个位置，那么我们应该如何进行选择呢？直观上来看，我们可以「贪心」地选择距离最后一个位置最远的那个位置，也就是对应下标最小的那个位置。因此，我们可以从左到右遍历数组，选择第一个满足要求的位置。

找到最后一步跳跃前所在的位置之后，我们继续贪心地寻找倒数第二步跳跃前所在的位置，以此类推，直到找到数组的开始位置。
class Solution {
    public int jump(int[] nums) {
        int position = nums.length - 1;
        int steps = 0;
        while (position > 0) {
            for (int i = 0; i < position; i++) {
                if (i + nums[i] >= position) {
                    position = i;
                    steps++;
                    break;
                }
            }
        }
        return steps;
    }
}

77.H 指数

给你一个整数数组 citations ，其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。

根据维基百科上 h 指数的定义：h 代表“高引用次数” ，一名科研人员的 h 指数 是指他（她）至少发表了 h 篇论文，并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值，h 指数 是其中最大的那个。

方法一：排序
首先我们可以将初始的 H 指数 h 设为 0，然后将引用次数排序，并且对排序后的数组从大到小遍历。

根据 H 指数的定义，如果当前 H 指数为 h 并且在遍历过程中找到当前值 citations[i]>h，则说明我们找到了一篇被引用了至少 h+1 次的论文，所以将现有的 h 值加 1。继续遍历直到 h 无法继续增大。最后返回 h 作为最终答案。

class Solution {
    public int hIndex(int[] citations) {
        Arrays.sort(citations);
        int h = 0, i = citations.length - 1; 
        while (i >= 0 && citations[i] > h) {
            h++; 
            i--;
        }
        return h;
    }
}

78.除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

方法一：左右乘积列表
思路
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案，而是利用索引左侧所有数字的乘积和右侧所有数字的乘积（即前缀与后缀）相乘得到答案。
对于给定索引 i，我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。

初始化两个空数组 L 和 R。对于给定索引 i，L[i] 代表的是 i 左侧所有数字的乘积，R[i] 代表的是 i 右侧所有数字的乘积。
我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L，L[0] 应该是 1，因为第一个元素的左边没有元素。对于其他元素：L[i] = L[i-1] * nums[i-1]。
同理，对于数组 R，R[length-1] 应为 1。length 指的是输入数组的大小。其他元素：R[i] = R[i+1] * nums[i+1]。
当 R 和 L 数组填充完成，我们只需要在输入数组上迭代，且索引 i 处的值为：L[i] * R[i]。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        int length = nums.length;

        // L 和 R 分别表示左右两侧的乘积列表
        int[] L = new int[length];
        int[] R = new int[length];

        int[] answer = new int[length];

        // L[i] 为索引 i 左侧所有元素的乘积
        // 对于索引为 '0' 的元素，因为左侧没有元素，所以 L[0] = 1
        L[0] = 1;
        for (int i = 1; i < length; i++) {
            L[i] = nums[i - 1] * L[i - 1];
        }

        // R[i] 为索引 i 右侧所有元素的乘积
        // 对于索引为 'length-1' 的元素，因为右侧没有元素，所以 R[length-1] = 1
        R[length - 1] = 1;
        for (int i = length - 2; i >= 0; i--) {
            R[i] = nums[i + 1] * R[i + 1];
        }

        // 对于索引 i，除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
        for (int i = 0; i < length; i++) {
            answer[i] = L[i] * R[i];
        }

        return answer;
    }
}

79.加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

方法一：一次遍历
思路与算法

最容易想到的解法是：从头到尾遍历每个加油站，并检查以该加油站为起点，最终能否行驶一周。我们可以通过减小被检查的加油站数目，来降低总的时间复杂度。

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int n = gas.length;
        int i = 0;
        while (i < n) {
            int sumOfGas = 0, sumOfCost = 0;
            int cnt = 0;
            while (cnt < n) {
                int j = (i + cnt) % n;
                sumOfGas += gas[j];
                sumOfCost += cost[j];
                if (sumOfCost > sumOfGas) {
                    break;
                }
                cnt++;
            }
            if (cnt == n) {
                return i;
            } else {
                i = i + cnt + 1;
            }
        }
        return -1;
    }
}

80.三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

方法一：排序 + 双指针
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 枚举 a
        for (int first = 0; first < n; ++first) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            // c 对应的指针初始指向数组的最右端
            int third = n - 1;
            int target = -nums[first];
            // 枚举 b
            for (int second = first + 1; second < n; ++second) {
                // 需要和上一次枚举的数不相同
                if (second > first + 1 && nums[second] == nums[second - 1]) {
                    continue;
                }
                // 需要保证 b 的指针在 c 的指针的左侧
                while (second < third && nums[second] + nums[third] > target) {
                    --third;
                }
                // 如果指针重合，随着 b 后续的增加
                // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环
                if (second == third) {
                    break;
                }
                if (nums[second] + nums[third] == target) {
                    List<Integer> list = new ArrayList<Integer>();
                    list.add(nums[first]);
                    list.add(nums[second]);
                    list.add(nums[third]);
                    ans.add(list);
                }
            }
        }
        return ans;
    }
}

81.无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

方法一：滑动窗口
思路和算法

我们先用一个例子考虑如何在较优的时间复杂度内通过本题。

我们不妨以示例一中的字符串 abcabcbb 为例，找出从每一个字符开始的，不包含重复字符的最长子串，那么其中最长的那个字符串即为答案。对于示例一中的字符串，我们列举出这些结果，其中括号中表示选中的字符以及最长的字符串：

以 (a)bcabcbb 开始的最长字符串为 (abc)abcbb；
以 a(b)cabcbb 开始的最长字符串为 a(bca)bcbb；
以 ab(c)abcbb 开始的最长字符串为 ab(cab)cbb；
以 abc(a)bcbb 开始的最长字符串为 abc(abc)bb；
以 abca(b)cbb 开始的最长字符串为 abca(bc)bb；
以 abcab(c)bb 开始的最长字符串为 abcab(cb)b；
以 abcabc(b)b 开始的最长字符串为 abcabc(b)b；
以 abcabcb(b) 开始的最长字符串为 abcabcb(b)。
发现了什么？如果我们依次递增地枚举子串的起始位置，那么子串的结束位置也是递增的！这里的原因在于，假设我们选择字符串中的第 k 个字符作为起始位置，并且得到了不包含重复字符的最长子串的结束位置为 r 
k
​
 。那么当我们选择第 k+1 个字符作为起始位置时，首先从 k+1 到 r 
k
​
  的字符显然是不重复的，并且由于少了原本的第 k 个字符，我们可以尝试继续增大 r 
k
​
 ，直到右侧出现了重复字符为止。

这样一来，我们就可以使用「滑动窗口」来解决这个问题了：

我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界，其中左指针代表着上文中「枚举子串的起始位置」，而右指针即为上文中的 r 
k
​
 ；

在每一步的操作中，我们会将左指针向右移动一格，表示 我们开始枚举下一个字符作为起始位置，然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后，这个子串就对应着 以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；

在枚举结束后，我们找到的最长的子串的长度即为答案。

判断重复字符

在上面的流程中，我们还需要使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合（即 C++ 中的 std::unordered_set，Java 中的 HashSet，Python 中的 set, JavaScript 中的 Set）。在左指针向右移动的时候，我们从哈希集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。
class Solution {
    public int lengthOfLongestSubstring(String s) {
        // 哈希集合，记录每个字符是否出现过
        Set<Character> occ = new HashSet<Character>();
        int n = s.length();
        // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
        int rk = -1, ans = 0;
        for (int i = 0; i < n; ++i) {
            if (i != 0) {
                // 左指针向右移动一格，移除一个字符
                occ.remove(s.charAt(i - 1));
            }
            while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
                // 不断地移动右指针
                occ.add(s.charAt(rk + 1));
                ++rk;
            }
            // 第 i 到 rk 个字符是一个极长的无重复字符子串
            ans = Math.max(ans, rk - i + 1);
        }
        return ans;
    }
}

82.有效的数独

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

方法一：一次遍历
有效的数独满足以下三个条件：

同一个数字在每一行只能出现一次；

同一个数字在每一列只能出现一次；

同一个数字在每一个小九宫格只能出现一次。

可以使用哈希表记录每一行、每一列和每一个小九宫格中，每个数字出现的次数。只需要遍历数独一次，在遍历的过程中更新哈希表中的计数，并判断是否满足有效的数独的条件即可。

class Solution {
    public boolean isValidSudoku(char[][] board) {
        int[][] rows = new int[9][9];
        int[][] columns = new int[9][9];
        int[][][] subboxes = new int[3][3][9];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                if (c != '.') {
                    int index = c - '0' - 1;
                    rows[i][index]++;
                    columns[j][index]++;
                    subboxes[i / 3][j / 3][index]++;
                    if (rows[i][index] > 1 || columns[j][index] > 1 || subboxes[i / 3][j / 3][index] > 1) {
                        return false;
                    }
                }
            }
        }
        return true;
    }
}

83.生命游戏

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

方法一：复制原数组进行模拟
思路

这个问题看起来很简单，但有一个陷阱，如果你直接根据规则更新原始数组，那么就做不到题目中说的 同步 更新。假设你直接将更新后的细胞状态填入原始数组，那么当前轮次其他细胞状态的更新就会引用到当前轮已更新细胞的状态，但实际上每一轮更新需要依赖上一轮细胞的状态，是不能用这一轮的细胞状态来更新的。

class Solution {
    public void gameOfLife(int[][] board) {
        int[] neighbors = {0, 1, -1};

        int rows = board.length;
        int cols = board[0].length;

        // 创建复制数组 copyBoard
        int[][] copyBoard = new int[rows][cols];

        // 从原数组复制一份到 copyBoard 中
        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {
                copyBoard[row][col] = board[row][col];
            }
        }

        // 遍历面板每一个格子里的细胞
        for (int row = 0; row < rows; row++) {
            for (int col = 0; col < cols; col++) {

                // 对于每一个细胞统计其八个相邻位置里的活细胞数量
                int liveNeighbors = 0;

                for (int i = 0; i < 3; i++) {
                    for (int j = 0; j < 3; j++) {

                        if (!(neighbors[i] == 0 && neighbors[j] == 0)) {
                            int r = (row + neighbors[i]);
                            int c = (col + neighbors[j]);

                            // 查看相邻的细胞是否是活细胞
                            if ((r < rows && r >= 0) && (c < cols && c >= 0) && (copyBoard[r][c] == 1)) {
                                liveNeighbors += 1;
                            }
                        }
                    }
                }

                // 规则 1 或规则 3      
                if ((copyBoard[row][col] == 1) && (liveNeighbors < 2 || liveNeighbors > 3)) {
                    board[row][col] = 0;
                }
                // 规则 4
                if (copyBoard[row][col] == 0 && liveNeighbors == 3) {
                    board[row][col] = 1;
                }
            }
        }
    }
}

84.赎金信

给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成。

如果可以，返回 true ；否则返回 false 。

magazine 中的每个字符只能在 ransomNote 中使用一次。

方法一：字符统计
题目要求使用字符串 magazine 中的字符来构建新的字符串 ransomNote，且ransomNote 中的每个字符只能使用一次，只需要满足字符串 magazine 中的每个英文字母 (’a’-’z’) 的统计次数都大于等于 ransomNote 中相同字母的统计次数即可。

如果字符串 magazine 的长度小于字符串 ransomNote 的长度，则我们可以肯定 magazine 无法构成 ransomNote，此时直接返回 false。
首先统计 magazine 中每个英文字母 a 的次数 cnt[a]，再遍历统计 ransomNote 中每个英文字母的次数，如果发现 ransomNote 中存在某个英文字母 c 的统计次数大于 magazine 中该字母统计次数 cnt[c]，则此时我们直接返回 false。

class Solution {
    public boolean canConstruct(String ransomNote, String magazine) {
        if (ransomNote.length() > magazine.length()) {
            return false;
        }
        int[] cnt = new int[26];
        for (char c : magazine.toCharArray()) {
            cnt[c - 'a']++;
        }
        for (char c : ransomNote.toCharArray()) {
            cnt[c - 'a']--;
            if(cnt[c - 'a'] < 0) {
                return false;
            }
        }
        return true;
    }
}

85.同构字符串

给定两个字符串 s 和 t ，判断它们是否是同构的。

如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。

每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。

方法一：哈希表
此题是「290. 单词规律」的简化版，需要我们判断 s 和 t 每个位置上的字符是否都一一对应，即 s 的任意一个字符被 t 中唯一的字符对应，同时 t 的任意一个字符被 s 中唯一的字符对应。这也被称为「双射」的关系。

以示例 2 为例，t 中的字符 a 和 r 虽然有唯一的映射 o，但对于 s 中的字符 o 来说其存在两个映射 {a,r}，故不满足条件。

因此，我们维护两张哈希表，第一张哈希表 s2t 以 s 中字符为键，映射至 t 的字符为值，第二张哈希表 t2s 以 t 中字符为键，映射至 s 的字符为值。从左至右遍历两个字符串的字符，不断更新两张哈希表，如果出现冲突（即当前下标 index 对应的字符 s[index] 已经存在映射且不为 t[index] 或当前下标 index 对应的字符 t[index] 已经存在映射且不为 s[index]）时说明两个字符串无法构成同构，返回 false。

如果遍历结束没有出现冲突，则表明两个字符串是同构的，返回 true 即可

class Solution {
    public boolean isIsomorphic(String s, String t) {
        Map<Character, Character> s2t = new HashMap<Character, Character>();
        Map<Character, Character> t2s = new HashMap<Character, Character>();
        int len = s.length();
        for (int i = 0; i < len; ++i) {
            char x = s.charAt(i), y = t.charAt(i);
            if ((s2t.containsKey(x) && s2t.get(x) != y) || (t2s.containsKey(y) && t2s.get(y) != x)) {
                return false;
            }
            s2t.put(x, y);
            t2s.put(y, x);
        }
        return true;
    }
}

86.单词规律

给定一种规律 pattern 和一个字符串 s ，判断 s 是否遵循相同的规律。

这里的 遵循 指完全匹配，例如， pattern 里的每个字母和字符串 s 中的每个非空单词之间存在着双向连接的对应规律。

方法一：哈希表
思路及解法

在本题中，我们需要判断字符与字符串之间是否恰好一一对应。即任意一个字符都对应着唯一的字符串，任意一个字符串也只被唯一的一个字符对应。在集合论中，这种关系被称为「双射」。

想要解决本题，我们可以利用哈希表记录每一个字符对应的字符串，以及每一个字符串对应的字符。然后我们枚举每一对字符与字符串的配对过程，不断更新哈希表，如果发生了冲突，则说明给定的输入不满足双射关系。

在实际代码中，我们枚举 pattern 中的每一个字符，利用双指针来均摊线性地找到该字符在 str 中对应的字符串。每次确定一个字符与字符串的组合，我们就检查是否出现冲突，最后我们再检查两字符串是否比较完毕即可

class Solution {
    public boolean wordPattern(String pattern, String str) {
        Map<String, Character> str2ch = new HashMap<String, Character>();
        Map<Character, String> ch2str = new HashMap<Character, String>();
        int m = str.length();
        int i = 0;
        for (int p = 0; p < pattern.length(); ++p) {
            char ch = pattern.charAt(p);
            if (i >= m) {
                return false;
            }
            int j = i;
            while (j < m && str.charAt(j) != ' ') {
                j++;
            }
            String tmp = str.substring(i, j);
            if (str2ch.containsKey(tmp) && str2ch.get(tmp) != ch) {
                return false;
            }
            if (ch2str.containsKey(ch) && !tmp.equals(ch2str.get(ch))) {
                return false;
            }
            str2ch.put(tmp, ch);
            ch2str.put(ch, tmp);
            i = j + 1;
        }
        return i >= m;
    }
}

87.汇总区间

给定一个 无重复元素 的 有序 整数数组 nums 。

返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个范围但不属于 nums 的数字 x 。

列表中的每个区间范围 [a,b] 应该按如下格式输出：

“a->b” ，如果 a != b
“a” ，如果 a == b

方法一：一次遍历
我们从数组的位置 0 出发，向右遍历。每次遇到相邻元素之间的差值大于 1 时，我们就找到了一个区间。遍历完数组之后，就能得到一系列的区间的列表。

在遍历过程中，维护下标 low 和 high 分别记录区间的起点和终点，对于任何区间都有 low≤high。当得到一个区间时，根据 low 和 high 的值生成区间的字符串表示。

当 low<high 时，区间的字符串表示为 ‘‘low→high"；

当 low=high 时，区间的字符串表示为 ‘‘low"。

class Solution {
    public List<String> summaryRanges(int[] nums) {
        List<String> ret = new ArrayList<String>();
        int i = 0;
        int n = nums.length;
        while (i < n) {
            int low = i;
            i++;
            while (i < n && nums[i] == nums[i - 1] + 1) {
                i++;
            }
            int high = i - 1;
            StringBuffer temp = new StringBuffer(Integer.toString(nums[low]));
            if (low < high) {
                temp.append("->");
                temp.append(Integer.toString(nums[high]));
            }
            ret.add(temp.toString());
        }
        return ret;
    }
}

88.合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

方法一：排序
思路

如果我们按照区间的左端点排序，那么在排完序的列表中，可以合并的区间一定是连续的。如下图所示，标记为蓝色、黄色和绿色的区间分别可以合并成一个大区间，它们在排完序的列表中是连续的

class Solution {
    public int[][] merge(int[][] intervals) {
        if (intervals.length == 0) {
            return new int[0][2];
        }
        Arrays.sort(intervals, new Comparator<int[]>() {
            public int compare(int[] interval1, int[] interval2) {
                return interval1[0] - interval2[0];
            }
        });
        List<int[]> merged = new ArrayList<int[]>();
        for (int i = 0; i < intervals.length; ++i) {
            int L = intervals[i][0], R = intervals[i][1];
            if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
                merged.add(new int[]{L, R});
            } else {
                merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
            }
        }
        return merged.toArray(new int[merged.size()][]);
    }
}

89.插入区间

给你一个 无重叠的 ，按照区间起始端点排序的区间列表 intervals，其中 intervals[i] = [starti, endi] 表示第 i 个区间的开始和结束，并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval = [start, end] 表示另一个区间的开始和结束。

在 intervals 中插入区间 newInterval，使得 intervals 依然按照 starti 升序排列，且区间之间不重叠（如果有必要的话，可以合并区间）。

返回插入之后的 intervals。

注意 你不需要原地修改 intervals。你可以创建一个新数组然后返回它。

方法一：模拟
思路与算法

在给定的区间集合 X 互不重叠的前提下，当我们需要插入一个新的区间 S=[left,right] 时，我们只需要：

找出所有与区间 S 重叠的区间集合 X 
′
 ；
将 X 
′
  中的所有区间连带上区间 S 合并成一个大区间；
最终的答案即为不与 X 
′
  重叠的区间以及合并后的大区间。

class Solution {
    public int[][] insert(int[][] intervals, int[] newInterval) {
        int left = newInterval[0];
        int right = newInterval[1];
        boolean placed = false;
        List<int[]> ansList = new ArrayList<int[]>();
        for (int[] interval : intervals) {
            if (interval[0] > right) {
                // 在插入区间的右侧且无交集
                if (!placed) {
                    ansList.add(new int[]{left, right});
                    placed = true;                    
                }
                ansList.add(interval);
            } else if (interval[1] < left) {
                // 在插入区间的左侧且无交集
                ansList.add(interval);
            } else {
                // 与插入区间有交集，计算它们的并集
                left = Math.min(left, interval[0]);
                right = Math.max(right, interval[1]);
            }
        }
        if (!placed) {
            ansList.add(new int[]{left, right});
        }
        int[][] ans = new int[ansList.size()][2];
        for (int i = 0; i < ansList.size(); ++i) {
            ans[i] = ansList.get(i);
        }
        return ans;
    }
}

90.有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

方法一：栈
判断括号的有效性可以使用「栈」这一数据结构来解决。

我们遍历给定的字符串 s。当我们遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。

当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。

在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。

注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，省去后续的遍历判断过程。

class Solution {
    public boolean isValid(String s) {
        int n = s.length();
        if (n % 2 == 1) {
            return false;
        }

        Map<Character, Character> pairs = new HashMap<Character, Character>() {{
            put(')', '(');
            put(']', '[');
            put('}', '{');
        }};
        Deque<Character> stack = new LinkedList<Character>();
        for (int i = 0; i < n; i++) {
            char ch = s.charAt(i);
            if (pairs.containsKey(ch)) {
                if (stack.isEmpty() || stack.peek() != pairs.get(ch)) {
                    return false;
                }
                stack.pop();
            } else {
                stack.push(ch);
            }
        }
        return stack.isEmpty();
    }
}

91.简化路径

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 ‘/’ 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （…） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，‘//’）都被视为单个斜杠 ‘/’ 。 对于此问题，任何其他格式的点（例如，‘…’）均被视为文件/目录名称。

请注意，返回的 规范路径 必须遵循下述格式：

始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名（如果存在）不能 以 ‘/’ 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 ‘.’ 或 ‘…’）。
返回简化后得到的 规范路径 。

方法一：栈
思路与算法

我们首先将给定的字符串 path 根据 / 分割成一个由若干字符串组成的列表，记为 names。根据题目中规定的「规范路径的下述格式」，names 中包含的字符串只能为以下几种：

空字符串。例如当出现多个连续的 /，就会分割出空字符串；

一个点 .；

两个点 ..；

只包含英文字母、数字或 _ 的目录名。

对于「空字符串」以及「一个点」，我们实际上无需对它们进行处理，因为「空字符串」没有任何含义，而「一个点」表示当前目录本身，我们无需切换目录。

对于「两个点」或者「目录名」，我们则可以用一个栈来维护路径中的每一个目录名。当我们遇到「两个点」时，需要将目录切换到上一级，因此只要栈不为空，我们就弹出栈顶的目录。当我们遇到「目录名」时，就把它放入栈。

这样一来，我们只需要遍历 names 中的每个字符串并进行上述操作即可。在所有的操作完成后，我们将从栈底到栈顶的字符串用 / 进行连接，再在最前面加上 / 表示根目录，就可以得到简化后的规范路径。

class Solution {
    public String simplifyPath(String path) {
        String[] names = path.split("/");
        Deque<String> stack = new ArrayDeque<String>();
        for (String name : names) {
            if ("..".equals(name)) {
                if (!stack.isEmpty()) {
                    stack.pollLast();
                }
            } else if (name.length() > 0 && !".".equals(name)) {
                stack.offerLast(name);
            }
        }
        StringBuffer ans = new StringBuffer();
        if (stack.isEmpty()) {
            ans.append('/');
        } else {
            while (!stack.isEmpty()) {
                ans.append('/');
                ans.append(stack.pollFirst());
            }
        }
        return ans.toString();
    }
}

92.路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

方法一：广度优先搜索
思路及算法

首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        Queue<TreeNode> queNode = new LinkedList<TreeNode>();
        Queue<Integer> queVal = new LinkedList<Integer>();
        queNode.offer(root);
        queVal.offer(root.val);
        while (!queNode.isEmpty()) {
            TreeNode now = queNode.poll();
            int temp = queVal.poll();
            if (now.left == null && now.right == null) {
                if (temp == sum) {
                    return true;
                }
                continue;
            }
            if (now.left != null) {
                queNode.offer(now.left);
                queVal.offer(now.left.val + temp);
            }
            if (now.right != null) {
                queNode.offer(now.right);
                queVal.offer(now.right.val + temp);
            }
        }
        return false;
    }
}
方法二：递归
思路及算法

观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }
}

93.二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

方法一：中序遍历
class Solution {
    int pre;
    int ans;

    public int getMinimumDifference(TreeNode root) {
        ans = Integer.MAX_VALUE;
        pre = -1;
        dfs(root);
        return ans;
    }

    public void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        if (pre == -1) {
            pre = root.val;
        } else {
            ans = Math.min(ans, root.val - pre);
            pre = root.val;
        }
        dfs(root.right);
    }
}

94.课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

方法一：深度优先搜索
思路

我们可以将深度优先搜索的流程与拓扑排序的求解联系起来，用一个栈来存储所有已经搜索完成的节点。

对于一个节点 u，如果它的所有相邻节点都已经搜索完成，那么在搜索回溯到 u 的时候，u 本身也会变成一个已经搜索完成的节点。这里的「相邻节点」指的是从 u 出发通过一条有向边可以到达的所有节点。

假设我们当前搜索到了节点 u，如果它的所有相邻节点都已经搜索完成，那么这些节点都已经在栈中了，此时我们就可以把 u 入栈。可以发现，如果我们从栈顶往栈底的顺序看，由于 u 处于栈顶的位置，那么 u 出现在所有 u 的相邻节点的前面。因此对于 u 这个节点而言，它是满足拓扑排序的要求的。

这样以来，我们对图进行一遍深度优先搜索。当每个节点进行回溯的时候，我们把该节点放入栈中。最终从栈顶到栈底的序列就是一种拓扑排序。

class Solution {
    List<List<Integer>> edges;
    int[] visited;
    boolean valid = true;

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        edges = new ArrayList<List<Integer>>();
        for (int i = 0; i < numCourses; ++i) {
            edges.add(new ArrayList<Integer>());
        }
        visited = new int[numCourses];
        for (int[] info : prerequisites) {
            edges.get(info[1]).add(info[0]);
        }
        for (int i = 0; i < numCourses && valid; ++i) {
            if (visited[i] == 0) {
                dfs(i);
            }
        }
        return valid;
    }

    public void dfs(int u) {
        visited[u] = 1;
        for (int v: edges.get(u)) {
            if (visited[v] == 0) {
                dfs(v);
                if (!valid) {
                    return;
                }
            } else if (visited[v] == 1) {
                valid = false;
                return;
            }
        }
        visited[u] = 2;
    }
}

95.全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

方法一：回溯
这个问题可以看作有 n 个排列成一行的空格，我们需要从左往右依此填入题目给定的 n 个数，每个数只能使用一次。那么很直接的可以想到一种穷举的算法，即从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，在程序中我们可以用「回溯法」来模拟这个过程。

我们定义递归函数 backtrack(first,output) 表示从左往右填到第 first 个位置，当前排列为 output。 那么整个递归函数分为两个情况：

如果 first=n，说明我们已经填完了 n 个位置（注意下标从 0 开始），找到了一个可行的解，我们将 output 放入答案数组中，递归结束。
如果 first<n，我们要考虑这第 first 个位置我们要填哪个数。根据题目要求我们肯定不能填已经填过的数，因此很容易想到的一个处理手段是我们定义一个标记数组 vis 来标记已经填过的数，那么在填第 first 个数的时候我们遍历题目给定的 n 个数，如果这个数没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个位置，即调用函数 backtrack(first+1,output)。回溯的时候要撤销这一个位置填的数以及标记，并继续尝试其他没被标记过的数。
使用标记数组来处理填过的数是一个很直观的思路，但是可不可以去掉这个标记数组呢？毕竟标记数组也增加了我们算法的空间复杂度。

答案是可以的，我们可以将题目给定的 n 个数的数组 nums 划分成左右两个部分，左边的表示已经填过的数，右边表示待填的数，我们在回溯的时候只要动态维护这个数组即可。

具体来说，假设我们已经填到第 first 个位置，那么 nums 数组中 [0,first−1] 是已填过的数的集合，[first,n−1] 是待填的数的集合。我们肯定是尝试用 [first,n−1] 里的数去填第 first 个数，假设待填的数的下标为 i，那么填完以后我们将第 i 个数和第 first 个数交换，即能使得在填第 first+1 个数的时候 nums 数组的 [0,first] 部分为已填过的数，[first+1,n−1] 为待填的数，回溯的时候交换回来即能完成撤销操作。

举个简单的例子，假设我们有 [2,5,8,9,10] 这 5 个数要填入，已经填到第 3 个位置，已经填了 [8,9] 两个数，那么这个数组目前为 [8,9 ∣ 2,5,10] 这样的状态，分隔符区分了左右两个部分。假设这个位置我们要填 10 这个数，为了维护数组，我们将 2 和 10 交换，即能使得数组继续保持分隔符左边的数已经填过，右边的待填 [8,9,10 ∣ 2,5] 。

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();

        List<Integer> output = new ArrayList<Integer>();
        for (int num : nums) {
            output.add(num);
        }

        int n = nums.length;
        backtrack(n, output, res, 0);
        return res;
    }

    public void backtrack(int n, List<Integer> output, List<List<Integer>> res, int first) {
        // 所有数都填完了
        if (first == n) {
            res.add(new ArrayList<Integer>(output));
        }
        for (int i = first; i < n; i++) {
            // 动态维护数组
            Collections.swap(output, first, i);
            // 继续递归填下一个数
            backtrack(n, output, res, first + 1);
            // 撤销操作
            Collections.swap(output, first, i);
        }
    }
}

96.寻找峰值

峰值元素是指其值严格大于左右相邻值的元素。

给你一个整数数组 nums，找到峰值元素并返回其索引。数组可能包含多个峰值，在这种情况下，返回 任何一个峰值 所在位置即可。

你可以假设 nums[-1] = nums[n] = -∞ 。

你必须实现时间复杂度为 O(log n) 的算法来解决此问题。

方法一：寻找最大值
思路与算法

由于题目保证了 nums[i]

=nums[i+1]，那么数组 nums 中最大值两侧的元素一定严格小于最大值本身。因此，最大值所在的位置就是一个可行的峰值位置。

我们对数组 nums 进行一次遍历，找到最大值对应的位置即可。

class Solution {
    public int findPeakElement(int[] nums) {
        int idx = 0;
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] > nums[idx]) {
                idx = i;
            }
        }
        return idx;
    }
}

方法二：迭代爬坡
思路与算法

俗话说「人往高处走，水往低处流」。如果我们从一个位置开始，不断地向高处走，那么最终一定可以到达一个峰值位置。

因此，我们首先在 [0,n) 的范围内随机一个初始位置 i，随后根据 nums[i−1],nums[i],nums[i+1] 三者的关系决定向哪个方向走：

如果 nums[i−1]<nums[i]>nums[i+1]，那么位置 i 就是峰值位置，我们可以直接返回 i 作为答案；

如果 nums[i−1]<nums[i]<nums[i+1]，那么位置 i 处于上坡，我们需要往右走，即 i←i+1；

如果 nums[i−1]>nums[i]>nums[i+1]，那么位置 i 处于下坡，我们需要往左走，即 i←i−1；

如果 nums[i−1]>nums[i]<nums[i+1]，那么位置 i 位于山谷，两侧都是上坡，我们可以朝任意方向走。

如果我们规定对于最后一种情况往右走，那么当位置 i 不是峰值位置时：

如果 nums[i]<nums[i+1]，那么我们往右走；

如果 nums[i]>nums[i+1]，那么我们往左走。

class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        int idx = (int) (Math.random() * n);

        while (!(compare(nums, idx - 1, idx) < 0 && compare(nums, idx, idx + 1) > 0)) {
            if (compare(nums, idx, idx + 1) < 0) {
                idx += 1;
            } else {
                idx -= 1;
            }
        }
        
        return idx;
    }

    // 辅助函数，输入下标 i，返回一个二元组 (0/1, nums[i])
    // 方便处理 nums[-1] 以及 nums[n] 的边界情况
    public int[] get(int[] nums, int idx) {
        if (idx == -1 || idx == nums.length) {
            return new int[]{0, 0};
        }
        return new int[]{1, nums[idx]};
    }

    public int compare(int[] nums, int idx1, int idx2) {
        int[] num1 = get(nums, idx1);
        int[] num2 = get(nums, idx2);
        if (num1[0] != num2[0]) {
            return num1[0] > num2[0] ? 1 : -1;
        }
        if (num1[1] == num2[1]) {
            return 0;
        }
        return num1[1] > num2[1] ? 1 : -1;
    }
}

97.寻找旋转排序数组中的最小值

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

方法一：二分查找
class Solution {
    public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            } else {
                low = pivot + 1;
            }
        }
        return nums[low];
    }
}

98. 阶乘后的零

给定一个整数 n ，返回 n! 结果中尾随零的数量。

提示 n! = n * (n - 1) * (n - 2) * … * 3 * 2 * 1

方法一：数学
n! 尾零的数量即为 n! 中因子 10 的个数，而 10=2×5，因此转换成求 n! 中质因子 2 的个数和质因子 5 的个数的较小值。

由于质因子 5 的个数不会大于质因子 2 的个数（具体证明见方法二），我们可以仅考虑质因子 5 的个数。

而 n! 中质因子 5 的个数等于 [1,n] 的每个数的质因子 5 的个数之和，我们可以通过遍历 [1,n] 的所有 5 的倍数求出。

class Solution {
    public int trailingZeroes(int n) {
        int ans = 0;
        for (int i = 5; i <= n; i += 5) {
            for (int x = i; x % 5 == 0; x /= 5) {
                ++ans;
            }
        }
        return ans;
    }
}

99.买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

方法一：动态规划
思路与算法

由于我们最多可以完成两笔交易，因此在任意一天结束之后，我们会处于以下五个状态中的一种：

未进行过任何操作；

只进行过一次买操作；

进行了一次买操作和一次卖操作，即完成了一笔交易；

在完成了一笔交易的前提下，进行了第二次买操作；

完成了全部两笔交易。

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        int buy1 = -prices[0], sell1 = 0;
        int buy2 = -prices[0], sell2 = 0;
        for (int i = 1; i < n; ++i) {
            buy1 = Math.max(buy1, -prices[i]);
            sell1 = Math.max(sell1, buy1 + prices[i]);
            buy2 = Math.max(buy2, sell1 - prices[i]);
            sell2 = Math.max(sell2, buy2 + prices[i]);
        }
        return sell2;
    }
}

100.最大正方形

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

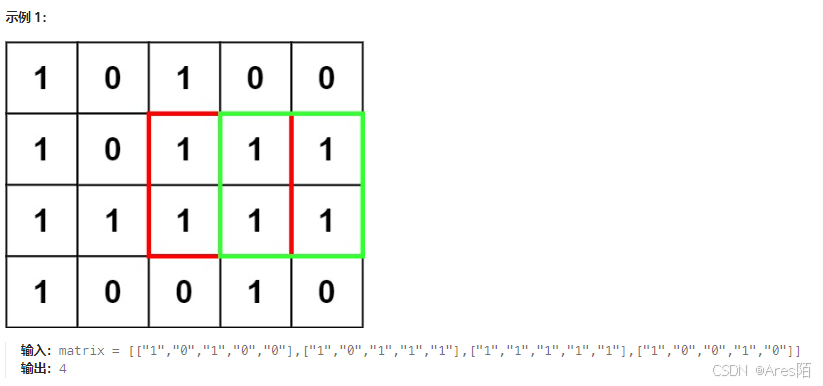
方法一：暴力法
由于正方形的面积等于边长的平方，因此要找到最大正方形的面积，首先需要找到最大正方形的边长，然后计算最大边长的平方即可。

暴力法是最简单直观的做法，具体做法如下：

遍历矩阵中的每个元素，每次遇到 1，则将该元素作为正方形的左上角；

确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围不能超出矩阵的行数和列数），在该边长范围内寻找只包含 1 的最大正方形；

每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 1。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    // 遇到一个 1 作为正方形的左上角
                    maxSide = Math.max(maxSide, 1);
                    // 计算可能的最大正方形边长
                    int currentMaxSide = Math.min(rows - i, columns - j);
                    for (int k = 1; k < currentMaxSide; k++) {
                        // 判断新增的一行一列是否均为 1
                        boolean flag = true;
                        if (matrix[i + k][j + k] == '0') {
                            break;
                        }
                        for (int m = 0; m < k; m++) {
                            if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0') {
                                flag = false;
                                break;
                            }
                        }
                        if (flag) {
                            maxSide = Math.max(maxSide, k + 1);
                        } else {
                            break;
                        }
                    }
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}