机器学习5-Logistic回归-CSDN博客

本文链接：https://blog.csdn.net/qq_15799355/article/details/52722927

机器学习5-Logistic回归

Sigmoid函数和逻辑回归分类器
最优化理论初步
梯度下降最优化算法
数据中的缺失项处理

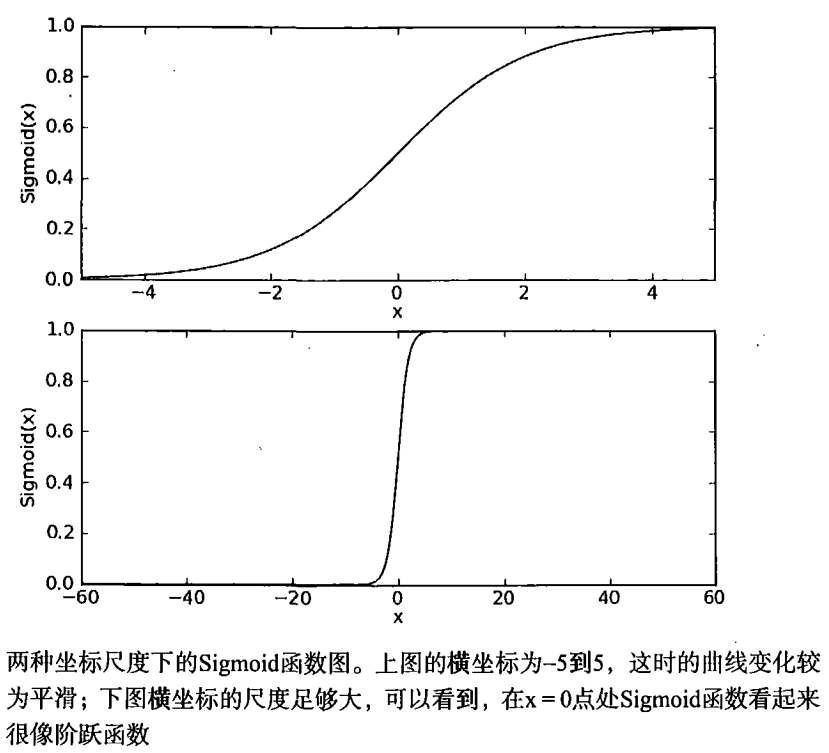
sigmoid函数

x>0         0.5<Sigmoid(x)=1
x<0         0=Sigmoid(x)<0.5

$\sigma(z)=\dfrac{1}{1+e^{-z}}$

梯度下降（上升）法（gradAscent）

梯度公式
这里写图片描述

背景知识（额外的，此部分可以最后再看）：
这里写图片描述

这里写图片描述

与批量梯度下降相比，随机梯度下降每次迭代只用到了一个样本，在样本量很大的情况下，常见的情况是只用到了其中一部分样本数据即可将θ迭代到最优解。因此随机梯度下降比批量梯度下降在计算量上会大大减少。

SGD有一个缺点是，其噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。而且SGD因为每次都是使用一个样本进行迭代，因此最终求得的最优解往往不是全局最优解，而只是局部最优解。但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

对比其优劣点如下：
批量梯度下降：
优点：全局最优解；易于并行实现；总体迭代次数不多
缺点：当样本数目很多时，训练过程会很慢，每次迭代需要耗费大量的时间。

随机梯度下降：
优点：训练速度快，每次迭代计算量不大
缺点：准确度下降，并不是全局最优；不易于并行实现；总体迭代次数比较多。

Logistic 回归梯度上升优化算法

example:testSet.txt
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
…

w e i g h t s = we i g h t s + alpha * d a t a M a t r i x .transpose()* error
$weights:=weights+\alpha{A^{T}error}$

from numpy import *


def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat


def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))


def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)  # convert to NumPy matrix
    labelMat = mat(classLabels).transpose()  # convert to NumPy matrix
    m, n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n, 1))
    for k in range(maxCycles):  # heavy on matrix operations
        h = sigmoid(dataMatrix * weights)  # matrix mult
        error = (labelMat - h)  # vector subtraction
        weights = weights + alpha * dataMatrix.transpose() * error  # matrix mult
    return weights

运行

>>> import logRegres
>>> dataMat, labelMat=logRegres.loadDataSet()
>>> w=logRegres.gradAscent(dataMat, labelMat)
>>> w
matrix([[ 4.12414349],
        [ 0.48007329],
        [-0.6168482 ]])

可视化

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = [];
    ycord1 = []
    xcord2 = [];
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1]);
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1]);
            ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]
    ax.plot(x, y)
    plt.xlabel('X1');
    plt.ylabel('X2');
    plt.show()

运行

from numpy import *
reload(logRegres)
weights=logRegres.gradAscent(dataArr,labelMat)
logRegres.plotBestFit(weights.getA()) #Matrix to Arrary

批处理

批处理：梯度上升，每次计算全部样本，固定轮数
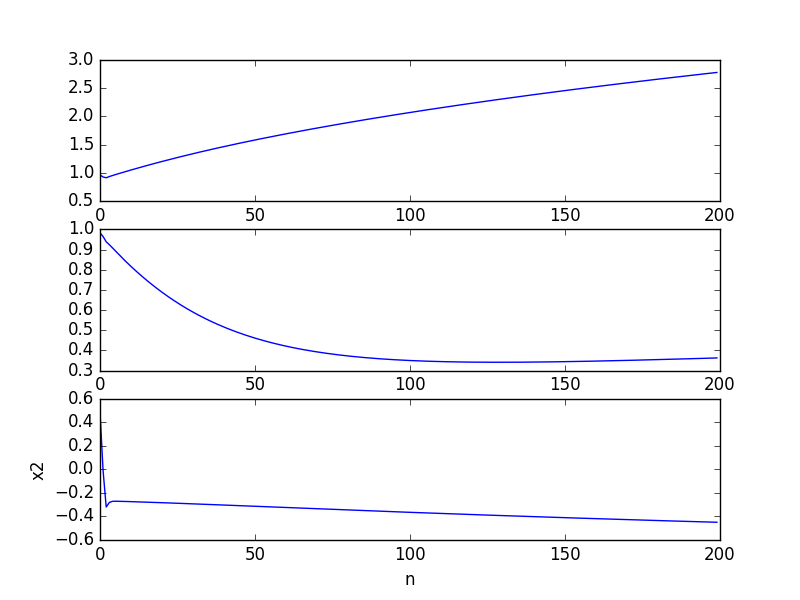
各权值变化速度图：

随机梯度上升（stochastic grad ascent）

在线学习法：随机梯度上升，每次计算一个样本，增量式计算

def stocGradAscent0(dataMatrix, classLabels):
    m, n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)  # initialize to all ones
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

运行

from numpy import *
reload(logRegres)
dataArr,labelMat=logRegres.loadDataSet()
weights=logRegres.stocGradAscent0(array(dataArr),labelMat)
logRegres.plotBestFit(weights)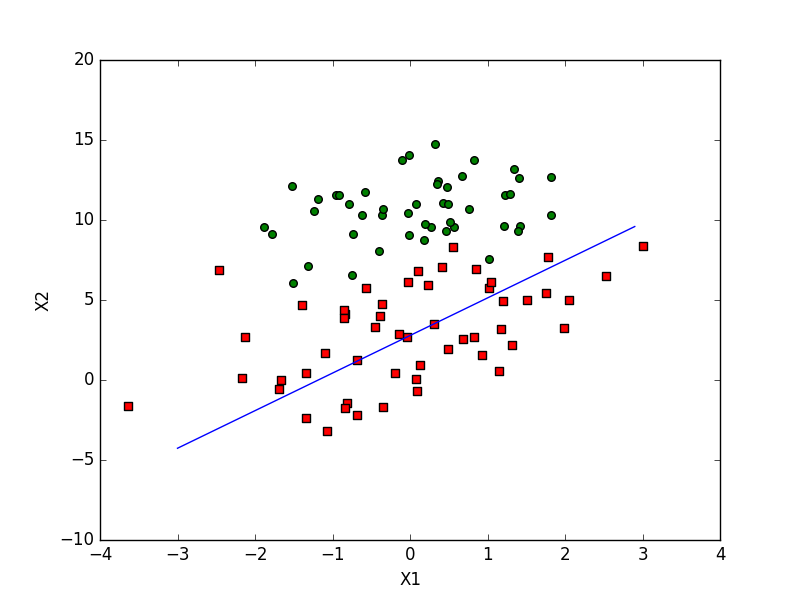

这里写图片描述
改进的随机梯度上升算法

步长变化
样本随机

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m, n = shape(dataMatrix)
    weights = ones(n)  # initialize to all ones
    for j in range(numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.0001  # apha decreases with iteration, does not
            randIndex = int(random.uniform(0, len(dataIndex)))  # go to 0 because of the constant
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del (dataIndex[randIndex])
    return weights

运行

from numpy import *
reload(logRegres)
dataArr,labelMat=logRegres.loadDataSet()
weights=logRegres.stocGradAscent1(array(dataArr),labelMat，20)
logRegres.plotBestFit(weights)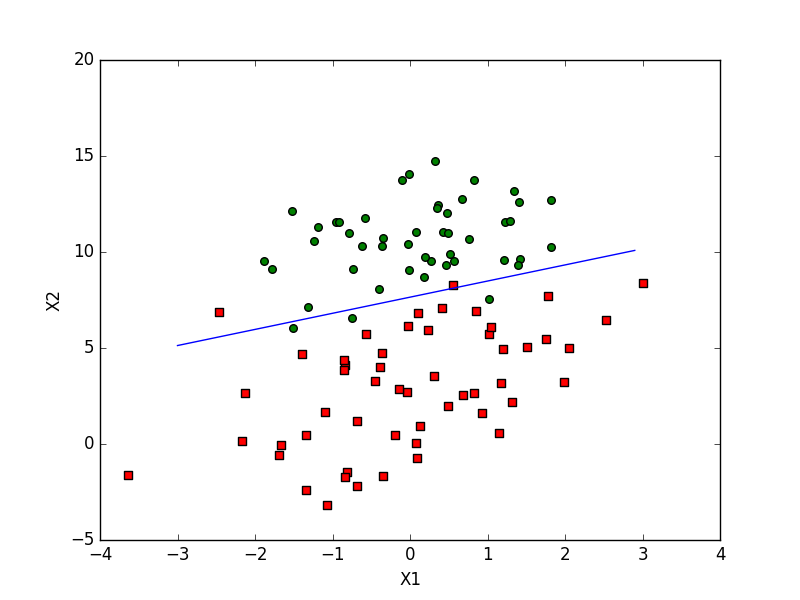

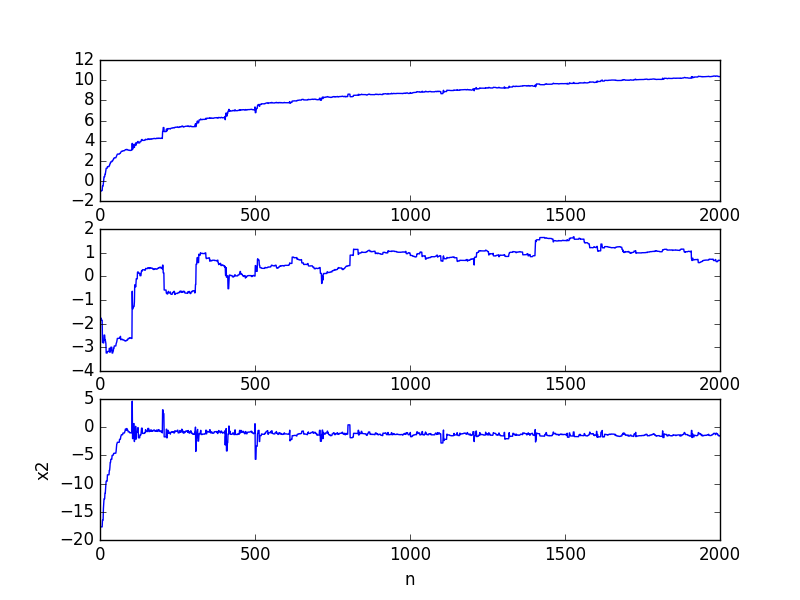
这里写图片描述
各权值变化速度图（20轮）：

处理数据中的缺失值

使用可用特征值的均值来填补
使用特殊值来填补（0，-1）
忽略所有含缺失值的样本（不可取）
使用相似样本的均值填补缺失值（难度高）
使用另外的机器学习算法预测缺失值（同上）

由于本章讨论梯度上升法，当特征值取0时不影响修改权值，相当于丢掉这条样本中缺失特征值部分而不是一条样本数据。
同时sigmoid函数当x=0时，值为0.5。不具有任何分类倾向。
因此本章采用0特殊值来填补缺失值。

注意：当类别标签丢失时，直接丢弃此样本。

示例：从疝气病症预测病马的死亡率
example ‘horseColicTraining.txt’：
2 1 38.50 54 20 0 1 2 2 3 4 1 2 2 5.90 0 2 42.00 6.30 0 0 1
2 1 37.60 48 36 0 0 1 1 0 3 0 0 0 0 0 0 44.00 6.30 1 5.00 1
…
example ‘horseColicTest.txt’：
2.000000 1.000000 38.500000 66.000000 28.000000 3.000000 3.000000 0.000000 2.000000 5.000000 4.000000 4.000000 0.000000 0.000000 0.000000 3.000000 5.000000 45.000000 8.400000 0.000000 0.000000 0.000000
1.000000 1.000000 39.200000 88.000000 20.000000 0.000000 0.000000 4.000000 1.000000 3.000000 4.000000 2.000000 0.000000 0.000000 0.000000 4.000000 2.000000 50.000000 85.000000 2.000000 2.000000 0.000000
…

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    if prob > 0.5:
        return 1.0
    else:
        return 0.0


def colicTest():
    frTrain = open('horseColicTraining.txt');
    frTest = open('horseColicTest.txt')
    trainingSet = [];
    trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet), trainingLabels, 1000)
    errorCount = 0;
    numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount) / numTestVec)
    print "the error rate of this test is: %f" % errorRate
    return errorRate


def multiTest():
    numTests = 10;
    errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests, errorSum / float(numTests))

运行结果

the error rate of this test is: 0.313433
the error rate of this test is: 0.328358
the error rate of this test is: 0.313433
the error rate of this test is: 0.388060
the error rate of this test is: 0.328358
the error rate of this test is: 0.358209
the error rate of this test is: 0.432836
the error rate of this test is: 0.238806
the error rate of this test is: 0.313433
the error rate of this test is: 0.358209
after 10 iterations the average error rate is: 0.337313

10次迭代后的平均误差为33%，这个结果还不错。如果调整随机梯度算法中的迭代轮数和步长，平均误差可以降到20%左右。

转自《机器学习实战》机器学习实战官网 Github代码地址
参考博客梯度下降法及其Python实现