不得不说,我已经卡在了这个原则两个周末了(因为只有周末有时间,平时加班回来基本洗澡完就睡死了,睡眠严重不足!)
看到刚刚才感觉能有点理解,这周末之前会把这篇日记补完,并附上代码。(嗯,已经立好flag了!)
啊哈哈哈,就知道flag这种鬼东西是真实有效了,我活活躺尸了两个月了。(每周只有半天一天的休息时间被基友什么鬼的占满了,加上几乎是一两周一次的通宵干活,搞的整个人都不成样了,精神状态好差,成天只想睡觉,日渐消瘦。)
Liskov替换原则:
子类型必须能够替换他们的基类型
举个栗子:
在数学上,正方形,长方形都是矩形,正方形是矩形中一个特殊的存在,长宽相等。那么我们将矩形定义为基类
//创建基类 矩形
class Rectangle
{
private double width;
private double height;
public double Width
{
get{ return width;}
set{ width = value;}
}
public double Height
{
get{ return height;}
set{ height = value;}
}
}
//1.当创建长方形时,继承基类,条件符合。(因为长方形的长跟宽与基类矩形一致,各自控制。)
//2.当创建正方形时,继承基类,条件不符合。(正方形的只有一条边,而矩形是控制两条边边,在特定情况下,使用基类调用的话,会出问题)
如:
class Rectangle
{
...
public void Area()
{
Console.WriteLine("矩形的面积:"+(width * height));
}
}
//长方形设置对应长宽,调用该方法时,得出的结果是所预期的。
//正方形设置边长(长或宽中的一个),调用该方法时,得出的结果并非预期中的值。因为矩形的算法是 长 * 宽 = 面积。而正方形只有一个边,这种情况下,我们可以通过以下方式解决(但治标不治本,依旧不是最佳的处理方式)
class Square : Rectangle
{
//基类的该方法记得加上 virtual
public override double Width
{
set
{
base.width = value;
base.height = value;
}
}
public override double Height
{
set
{
base.width = value;
base.height = value;
}
}
}
//为什么会治标不治本呢?看下面这个方法
void g (Rectangle r)
{
r.Width = 5;
r.Height = 4;
if (r.Area() != 20)
{
throw new Exception("该矩形有问题!");
}
}
//这就是问题所在~看完例子后,就可以得出以下的结论了。
这里的子类型(也就是基类型的派生类 ,这是个人理解,也不确定是否有误)必须遵循以下规则:
在重新声明派生类中的例程时只能使用相等或者更弱的牵制条件来替换原始的前置条件,只能使用相等或或者更强的后置条件来替换原始的后置条件。
按上面的例子而言,就是,正方形 setter的后置条件比基类的弱(也就是,子类没有遵从基类的的约束,这就称为弱。)
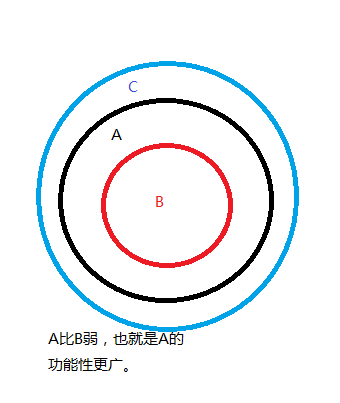
画个图 ,可以比较好理解一些。
前置条件:假设A是基类,B是各种各样的子类,A可以任意调用各种B来执行各种行为,也就是,B可以是A也可以是继承A的派生类。
后置条件:假设A是基类的约束条件,那么子类必须符合A或比A更小(强)的约束。(C比A的约束弱,所以C的违反了A定下的约束。)
大概这样子了。躺两个月了,还是要起来诈尸一下的。坐等悦天王检查作业,希望我的理解没错!
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








