转载自ACMdreamer的博客:<a target=_blank href="http://blog.csdn.net/acdreamers/article/details/8883285" target="_blank">http://blog.csdn.net/acdreamers/article/details/8883285</a> 定义:设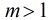
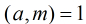

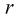
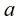

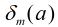
定理:如果模
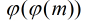
定理:若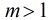
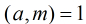
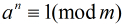
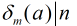
定理:如果


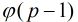
定理:设



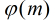


假设一个数

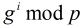
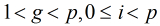


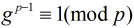


模
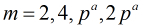
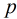
求模素数

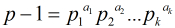

成立,则

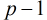
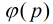
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>
#include <bitset>
using namespace std;
typedef long long LL;
const int N = 1000010;
bitset<N> prime;
int p[N],pri[N];
int k,cnt;
void isprime()
{
prime.set();
for(int i=2; i<N; i++)
{
if(prime[i])
{
p[k++] = i;
for(int j=i+i; j<N; j+=i)
prime[j] = false;
}
}
}
void Divide(int n)
{
cnt = 0;
int t = (int)sqrt(1.0*n);
for(int i=0; p[i]<=t; i++)
{
if(n%p[i]==0)
{
pri[cnt++] = p[i];
while(n%p[i]==0) n /= p[i];
}
}
if(n > 1)
pri[cnt++] = n;
}
LL quick_mod(LL a,LL b,LL m)
{
LL ans = 1;
a %= m;
while(b)
{
if(b&1)
{
ans = ans * a % m;
b--;
}
b >>= 1;
a = a * a % m;
}
return ans;
}
int main()
{
int P;
isprime();
while(cin>>P)
{
Divide(P-1);
for(int g=2; g<P; g++)
{
bool flag = true;
for(int i=0; i<cnt; i++)
{
int t = (P - 1) / pri[i];
if(quick_mod(g,t,P) == 1)
{
flag = false;
break;
}
}
if(flag)
{
int root = g;
cout<<root<<endl;
}
}
}
return 0;
}








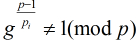
















 260
260

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








