Leetcode 1388：3n块披萨（超详细的解法！！！）

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

• 你挑选 任意 一块披萨。
• Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
• Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
• 重复上述过程直到没有披萨剩下。

每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

示例 1：

输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

示例 2：

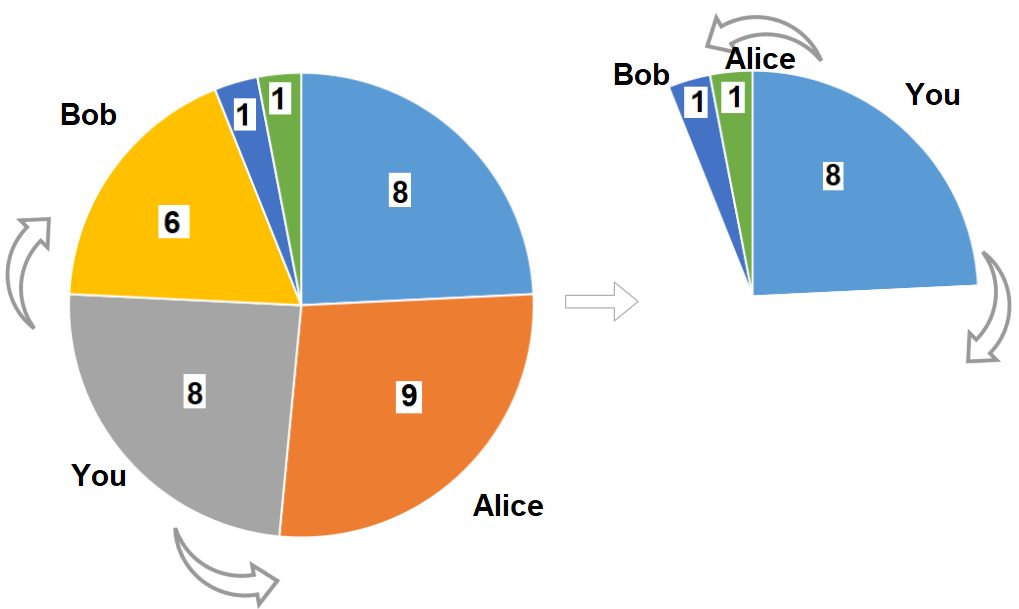
输入：slices = [8,9,8,6,1,1]
输出：16
解释：两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨，你的朋友们就会选择大小为 8 的披萨，这种情况下你的总和不是最大的。

示例 3：

输入：slices = [4,1,2,5,8,3,1,9,7]
输出：21

示例 4：

输入：slices = [3,1,2]
输出：3

提示：

• 1 <= slices.length <= 500
• slices.length % 3 == 0
• 1 <= slices[i] <= 1000

解题思路

这个问题和之前问题Leetcode 213：打家劫舍 II类似，区别在于这个问题中我们只可以选n//3个数，而之前的问题可以选(n-1)//2个数，但是思路相同。

对着这种环形问题只需分成两种情况讨论：1）第一个位置选。 2）最后一个位置选。（本质就是保证首尾不相邻）

该过程就是将环形问题转为非环问题，非环问题就是Leetcode 198：打家劫舍有n//3个数限制的情况。

from functools import lru_cache
class Solution:
    def maxSizeSlices(self, nums: List[int]) -> int:
        n = len(nums)
        
        @lru_cache(None)
        def dfs(cur, r, k):
            if k == 0: return 0
            if cur >= r: return 0
            return max(dfs(cur + 1, r, k), dfs(cur + 2, r, k - 1) + nums[cur])
        return max(dfs(0, n - 1, n // 3), dfs(1, n, n // 3))

按照和之前问题相同的处理手法，可以写出相应的动态规划形式。

class Solution:
    def maxSizeSlices(self, nums: List[int]) -> int:
        n = len(nums)
        k = n // 3
        
        def cal(l, r):
            dp = [[0] * (k + 1) for _ in range(n + 2)]
            for i in range(l, r):
                for j in range(k):
                    dp[i][j] = max(dp[i - 1][j], dp[i - 2][j - 1] + nums[i])
            return dp[r - 1][k - 1]
        return max(cal(0, n - 1), cal(1, n))

采用和之前问题相同的思路优化空间复杂度。

class Solution:
    def maxSizeSlices(self, nums: List[int]) -> int:
        n = len(nums)
        k = n // 3
        
        def cal(l, r):
            dp = [[0] * (k + 1) for _ in range(2)] 
            for i in range(l, r):
                
                dp[0], dp[1] = dp[1], [j and max(nums[i] + dp[0][j - 1], dp[1][j]) for j in range(k + 1)]
            return dp[-1][-1]
        return max(cal(0, n - 1), cal(1, n))

上面两种写法比较特别，第一种写法充分利用python的切片特性，可以通过-1访问最后一个元素，这一样我们就不同考虑j=0的情况。第二种写法为了维护空间大小的一致性，通过j and ...表达式判断j=0的情况。如果也想像第一种那样去写的话，可以这样：

dp[0], dp[1] = dp[1], [max(nums[i] + dp[0][j - 1], dp[1][j]) for j in range(k)] + [0]

或者可以用采用更一般性的写法：

class Solution:
    def maxSizeSlices(self, nums: List[int]) -> int:
        n = len(nums)
        k = n // 3
        
        def cal(l, r):
            dp = [[0] * (k + 1) for _ in range(2)]
            for i in range(l, r):
                for j in range(k, 0, -1):
                    dp[0][j] = dp[1][j]
                    dp[1][j] = max(dp[1][j], dp[0][j - 1] + nums[i])
            return dp[1][k]
        return max(cal(0, n - 1), cal(1, n))

其实质就是计算顺序的考虑。

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！