《视觉slam十四讲》笔记及课后习题-第3讲--刚体旋转

本文链接：https://blog.csdn.net/qq_18283857/article/details/106397266

目标

1、理论：理解三维空间的刚体运动的表达方法
2、实践：掌握Eigen库的矩阵、几何模块的使用方法

本人专业与惯导相关，接触过较多的惯导运动，故笔记重点在实践部分

理论部分

主要侧重于旋转的定义和表示方法

旋转矩阵

讲述了旋转的矩阵表示，齐次坐标和变换矩阵是我没有接触过的新知识。这样把旋转和平移统一在了一个矩阵中，使得多次变换维持线性关系。

三维形式多次变换不能维持线性关系
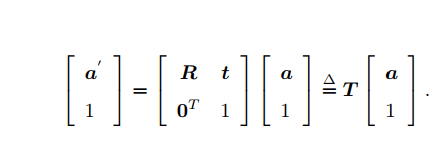
四维形式的变换矩阵使得变换为线性
齐次坐标比三维坐标多了一个自由度，[1 1 1 1]^T,和[2 2 2 2]^T表示的是同一个坐标，两者的变换关系如下
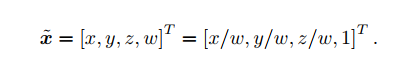
三维坐标和齐次坐标的变换关系
变换矩阵不是正交矩阵，其逆表示反向变换
变换矩阵的逆

旋转向量和欧拉角

旋转矩阵表示法的缺点：1、冗余度太高，9个量表示3个自由 2、9个量间有约束

旋转向量

	利用一个旋转轴（3）和一个旋转角（1）来刻画旋转，旋转向量和到旋转矩阵的公式
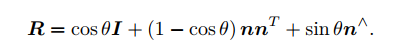
	![在这里插入图片描述](https://img-blog.csdnimg.cn/20200528105728692.png)
	旋转矩阵到旋转向量的转换过程分两步，对于转角
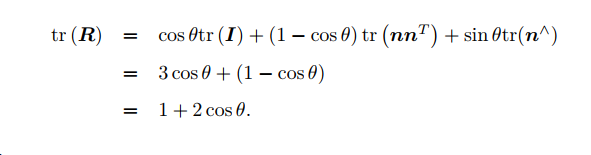
	![在这里插入图片描述](https://img-blog.csdnimg.cn/20200528105837939.png)
	对于旋转旋转轴，由于旋转轴经过旋转后不变的性质，说明
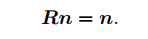
	![在这里插入图片描述](https://img-blog.csdnimg.cn/202005281059242.png)
	因此，转轴*n*是矩阵***R***特征值1对应的特征向量，求解次方程再归一化即可得到旋转轴

欧拉角

欧拉角通过坐标轴的三个旋转角来表示三维旋转（3个量），形象直观，但是不可避免存在万向锁问题，容易发生奇异，因此一般不用于滤波或优化解算，而用于人机交互
在这里插入图片描述
我对本节中旋转向量会奇异的说法存疑

四元数

单位四元数能表示空间任意旋转

任意的旋转都可以由两个互为相反数的单位四元数表示
任意的反向旋转都可以由互为共轭的单位四元数表示
四元数到旋转矩阵的转换
在这里插入图片描述

实践部分

Eigen库

问题1

假设我有一个大的 Eigen 矩阵，我想把它的左上角 3 × 3 的块取出来，然后赋值为:I3×3。请编程实现此事
程序如下，本题主要使用block函数对子矩阵进行选取
block函数的两种格式
block(i,j,p,q)和block<i,j,p,q>,均表示从位置（i,j）开始选取大小为（p,q）的子矩阵，区别为前一种为动态大小，后一种为固定长度模式***我还没搞明白这两者的区别***
源程序片段如下

Matrix<double,MATRIX_SIZE, MATRIX_SIZE> matrix_NN;

matrix_NN = Matrix<double, MATRIX_SIZE, MATRIX_SIZE>::Random();

cout<<"original matrix = \n"<<matrix_NN<<endl;
cout<<"submatrix from (1,0) size(2,2) = \n"<<matrix_NN.block<2,2>(1,0)<<endl;

输出如下

original matrix = 
  0.680375  -0.604897 -0.0452059    0.83239  -0.967399
 -0.211234  -0.329554   0.257742   0.271423  -0.514226
  0.566198   0.536459  -0.270431   0.434594  -0.725537
   0.59688  -0.444451  0.0268018  -0.716795   0.608354
  0.823295    0.10794   0.904459   0.213938  -0.686642
submatrix from (1,0) size(2,2) = 
-0.211234 -0.329554
 0.566198  0.536459

问题2

设有小萝卜一号和小萝卜二号位于世界坐标系中。小萝卜一号的位姿为： q1 =[0:35; 0:2; 0:3; 0:1]; t2 = [0:3; 0:1; 0:1]T（q 的第一项为实部请你把 q 归一化后再进行计算）。这里的 q 和 t 表达的是 Tcw，也就是世界到相机的变换关系。小萝卜二号的位姿为 q2 = [−0:5; 0:4; −0:1; 0:2]; t = [−0:1; 0:5; 0:3]T。现在，小萝卜一号看到某个点在自身的坐标系下，坐标为 p = [0:5; 0; 0:2]T，求该向量在小萝卜二号坐标系下的坐标。请编程实现此事

源程序

Quaterniond Q1(0.2, 0.3, 0.1, 0.35);
Quaterniond Q2(0.4,-0.1, 0.2, -0.5);//
Vector3d t1(0.3, 0.1, 0.1);
Vector3d t2(-0.1, 0.5, 0.3);
Vector3d p1(0.5, 0.0, 0.2);
Vector3d p2(0.0, 0.0, 0.0);

Q1.normalized();
Q2.normalized();

Isometry3d T1 = Isometry3d::Identity();//欧式变换矩阵
T1.rotate(Q1);
T1.pretranslate(t1);

Isometry3d T2 = Isometry3d::Identity();
T2.rotate(Q2);
T2.pretranslate(t2);

cout<<"T1 matrix = \n"<<T1.matrix()<<endl;

p2 = T2.inverse() * T1 * p1;

cout<<"the coordinate of p in camera 2 is = \n"<<p2<<endl;

输出结果

T1 matrix = 
0.735 -0.08  0.25   0.3
  0.2 0.575 -0.05   0.1
 0.17  0.19   0.8   0.1
    0     0     0     1
the coordinate of p in camera 2 is = 
0.47705
 0.1329
0.29025

强调文本 强调文本

加粗文本 加粗文本

标记文本

~~删除文本~~

引用文本

H₂O is是液体。

2¹⁰ 运算结果是 1024.

插入链接与图片

链接: link.

图片: Alt

带尺寸的图片:

居中的图片: Alt

居中并且带尺寸的图片:

当然，我们为了让用户更加便捷，我们增加了图片拖拽功能。

如何插入一段漂亮的代码片

去博客设置页面，选择一款你喜欢的代码片高亮样式，下面展示同样高亮的 代码片.

// An highlighted block
var foo = 'bar';

生成一个适合你的列表

项目
- 项目
  - 项目

项目1
项目2
项目3

计划任务
完成任务

创建一个表格

一个简单的表格是这么创建的：

项目	Value
电脑	$1600
手机	$12
导管	$1

设定内容居中、居左、居右

使用:---------:居中
使用:----------居左
使用----------:居右

第一列	第二列	第三列
第一列文本居中	第二列文本居右	第三列文本居左

SmartyPants

SmartyPants将ASCII标点字符转换为“智能”印刷标点HTML实体。例如：

TYPE	ASCII	HTML
Single backticks	`'Isn't this fun?'`	‘Isn’t this fun?’
Quotes	`"Isn't this fun?"`	“Isn’t this fun?”
Dashes	`-- is en-dash, --- is em-dash`	– is en-dash, — is em-dash