MTJ OJ-20

最新推荐文章于 2024-06-28 11:12:02 发布

Ving_L

最新推荐文章于 2024-06-28 11:12:02 发布

阅读量851

点赞数 3

分类专栏：码蹄集文章标签：算法

本文链接：https://blog.csdn.net/qq_18375019/article/details/127314976

版权

码蹄集专栏收录该内容

1 篇文章 1 订阅

订阅专栏

项链

难度：黄金

小码哥最近获得了n颗珍珠，第i颗珍珠拥有一个美观值a;。他现在想把这n颗珍珠以任意顺序排列后串成一串项链，定义一个项链的美观值为相邻珍珠的美观值之差的绝对值之和，即 $\sum_{i=1}^n{|a_{i}- a_{i+1}|}$

其中 $a_{i}$ 为重新排列后的项链上的第i颗珍珠的美观值，由于项链是一个环, 我们这里定义 $a_{n+1}=a_1$ 。
现在他想知道，在所有可能的情况下得到的项链的最大美观值为多少。请你编写一个程序帮助他计算一下这个值。

样例

输入

4
4 1 2 3

5
1 3 5 2 3

输出

题解

可知： $\sum_{i=1}^n{|a_{i}- a_{i+1}|} = |a_1 - a_2| + |a_2 - a_3| + .... + |a_n - a_{n+1}| + |a_{n+1} - a_1|$ ，
所以：
$Beautifulness= ±(a_1 - a_2) + ±（a_2 - a_3) + .... + ±(a_n - a_{n+1}) +± (a_{n+1} - a_1) = 2(±a_1 ± a_2 ±......± a_n ± a_{n+1})$

$2\sum_{i= 1}^{n+1}±a_i$
可以看出Beautifulness包含2n个数，并且2n个数里有n个正数和n和负数，现在问题转化成了：给定n个数，每个数可以出现两次，这些数里面需要有n个正数以及n个负数，求解2n个数和的最大值。

首先将数组 $a_i$ 从小到大排序
不难想到：当n为偶数时，最大值为：
$(\sum_{i = n/2}^{n}a_i - \sum_{i = 0}^{n/2-1}a_i)$
当n为奇数时，由于 $a_{n+1/2}$ 正负相加，导致结果为0
$2(\sum_{i = n+1/2}^{n}a_i - \sum_{i = 0}^{n/2-1}a_i)$

时间复杂度分析

预排序时间复杂度： $O (n l o g n)$
求和时间复杂度： $O (n)$
总体时间复杂度： $O (n l o g n)$

代码

#include<bits/stdc++.h> 

using namespace std;
const int maxn = 100005;
int a[maxn];
int main( )
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n;
    cin>>n;
    for (int i = 0;i<n;i++)
    {
        cin>>a[i];
    }
    sort(a,a+n);
    int sum1 = 0,sum2 = 0;
    for(int i = 0;i<n/2;i++)
    {
        sum1 += a[i];
    }
    if (n%2)    n++;
    for (int i = n/2;i<n;i++)
    {
        sum2 += a[i];
    }
    cout<<2*(sum2 - sum1);
    return 0;
}

圈竹鼠

难度：星耀

小码哥和小码弟兄弟俩决定改变饲养环境，给竹鼠更大的自由活动空间。现在竹鼠们在一块无限大的平面草地上，设某一定点坐标为(0, 0)，现在每只竹鼠都有自己最喜欢的地点，用坐标 (xi, yi) 表示。兄弟俩想用栅栏围住所有竹鼠喜欢的地点，现在请你计算他们能够围住这些地点的栅栏的最短长度。

格式

输入格式
输入数据的第一行是一个整数N,表示竹鼠最喜欢的地点数量。
接下来N行每行两个实数xi, yi表示对应地点坐标。
输出格式
输出一行保留两位小数的实数，代表围栏的长度。

样例

输入

输出

12.00

题解

采用Andrew求凸包问题的算法，由一个快排 $O (n l o g n)$ 和一个遍历找点 $O (n)$ ，总体时间复杂度为 $O (n l o g n)$ 。
快排：将所有点坐标由小到大排序，第一关键字为x，第二关键字为y
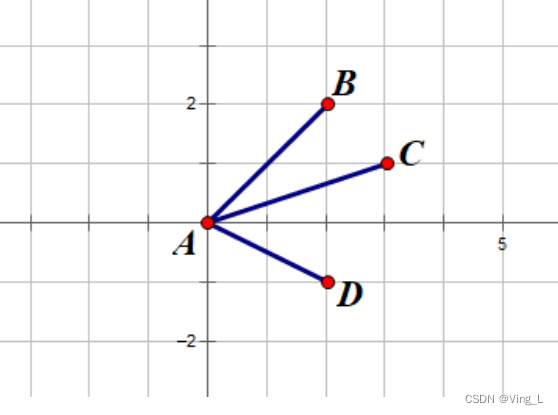
在这里插入图片描述

算法原理：对于向量 $A B$ 、 $A C$ ，.
若 $A B \times A C > 0$ ，则AB在AC的顺时针方向上
若 $A D \times A C > 0$ ，则AD在AC的逆时针方向上

算法步骤：建立一个存放点的栈

先把第一个点入栈
从预排序好的数组中顺序依次选点
若栈中只有一个点，直接将点入栈中
判断该点A与栈顶两个点（B,C）的向量叉乘乘积是否大于0（AC×AB>0）
大于0则把A入栈，小于0则从弹栈，重复3~5

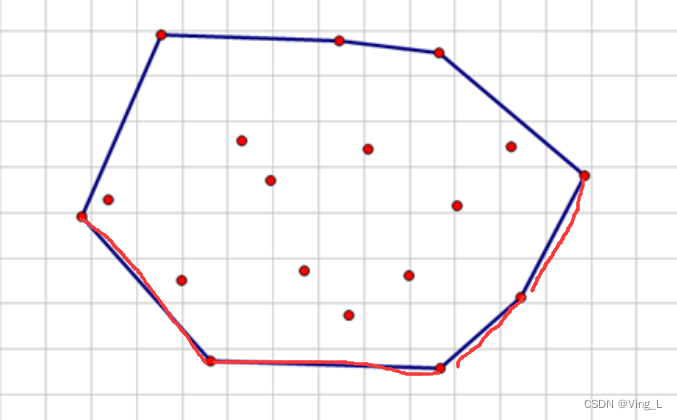
上述步骤只能求出整个凸包的一半（下半）。假设下凸包求出有k个点。
需要重复一遍上述流程（修改第2步为逆序选点、修改第三步若栈中只有k个点），即可求出整个凸包，凸包边缘的点最终存放在栈中。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 100005;
class point
{
public:
    double x,y;
    bool operator * (point a)
    {
        return x*a.y - y*a.x;
    }
    bool operator < (point a)
    {
        if (x < a.x)
            return true;
        else return x == a.x && y < a.y;
    }
    double dis(point a)
    {
        double dx = (x - a.x) * (x - a.x);
        double dy = (y - a.y) * (y - a.y);
        return sqrt(dx + dy);
    }
    static double xmul(point a,point b,point c)
    {
        return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x);
    }
};
point a[maxn],b[maxn];
int main( )
{
    int n;
    scanf("%d",&n);
    for (int i = 0;i<n;i++)
    {
        scanf("%lf %lf",&a[i].x,&a[i].y);
    }
    sort(a,a+n);
//    for (int i = 0;i<n;i++)
//    {
//        printf("%lf %lf\n",a[i].x,a[i].y);
//    }
    int cnt = 0;
    for(int i=0;i<n;++i)//计算下半个凸包
     {
        while(cnt >1 && point::xmul(b[cnt -2],b[cnt -1],a[i]) < 0)  --cnt;
        b[cnt++]=a[i];
     }

    int k=cnt;
    for(int i=n-2;i>=0;--i)//计算上半个凸包
    {
         while(cnt>k && point::xmul(b[cnt-2],b[cnt-1],a[i]) < 0)
             --cnt;
        b[cnt++]=a[i];
    }
    double ans = b[cnt-1].dis(b[0]);
    for (int i = 0;i<cnt-1;i++)
    {
        ans += b[i].dis(b[i+1]);
    }
    printf("%.2lf",ans);

    return 0;
}