前辍表达式，中辍表达式，后辍表达式详解

/*对于科学计算器的算法运用，有简单的算法也有难的算法，
比如我博客中的基本功能的算法代码，思维简单，但是代码编写起来却是麻烦有难度。
所以牛逼的大神么就搞出了几种牛逼的表达式，通过运用数据结构-栈-的优势，
充分的利用了他的递归性，达到了让人想象不到的高效率及便利性。
所以在这里给大家说说清楚，以免大家遇到问题时可以非常快的解决。
首先介绍一个概念，叫做中辍表达式
例子：
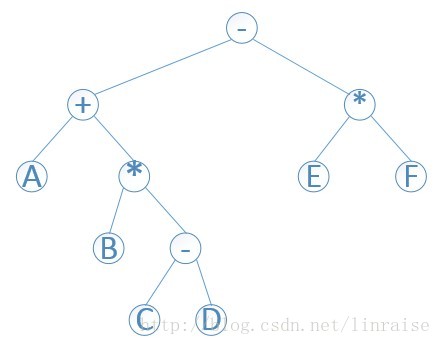
1+2-3*(4-5)
1+2*(3-4)-5*6
这些生活中，用于数学运算的就是中辍表达式
他可以用二叉树的形式表现出来。
下图是第一个式子的二叉树：*/

/*好，介绍完了简单的中辍表达式，开始介绍前辍表达式：
所谓的前辍表达式是指将运算符放在操作数的前面。
中辍表达式：1+2-3*(4-5)  ------>>>>>>>>前辍表达式：- + 1 2 * 3 - 4 5
用前辍表达式进行计算的方法，从左