HDU5575 Discover Water Tank 2015上海现场赛D题 （树形dp，并查集，左偏树）

题目大意：
有一个1维的长度为N，高度无限的水柜，现在要用N-1个挡板将其分为N个长度为1的小格，然后向水柜中注水，水可以低于挡板也可以以溢出去（这样就要与旁边格子的水位相同），现在有M次探测，探测i,y,k为查询第i个格子高度y+0.5处是否有水，k=1表示有水，k=0表示没有水，这M次探测不保证结果正确，现求结果正确个数的最大可能值。

思路：
这道题可以用类似树形dp的方法求解，依照分隔挡板由低到高的顺序将相邻的水柜合并，视为一个水柜，在合并前分别对两个水柜加水到刚好溢出，而对超出此水位的探测暂不处理，求出局部最优解（不溢出最优解f和溢出最优解g），并将各自未处理的探测合并为一个集合。不断进行此过程最后求出整个水柜的最优解。

主要操作为合并和注水，对每个水柜维护下列值：
注水高度h，不溢出最优解f，溢出最优解g，未处理探测集合E

以样例1为例说明处理方法

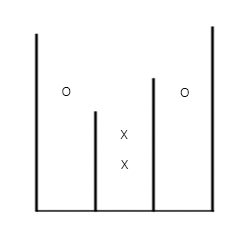
初状态
水柜1：h=0，f=0，g=0，E={<1,3,1>}
水柜2：h=0，f=0，g=0，E={<2,1,0>,<2,2,0>}
水柜3：h=0，f=0，g=0，E={<3,3,1>}

先将挡板由低到高排序
于是首先合并水柜1和水柜2，合并前先分别对两个水柜注水到挡板的高度3，
水柜1：h=3，f=0，g=0，E={<1,3,1>}
水柜2：h=3，f=2，g=0，E={}
合并后水柜1~2：h=3，f=2，g=0，E={<1,3,1>}

然后合并水柜1~2和水柜3，合并前先分别对两个水柜注水到挡板的高度4，
水柜1~2：h=4，f=2，g=1，E={}
水柜3：h=4，f=1，g=1，E={}
合并后水柜1~3：h=4，f=3，g=2，E={}

最后注水到最大值（比如1e9+5）
水柜1~3：h=4，f=3，g=2，E={}

于是得到结果为3

可以用并查集维护合并过程，用左斜树（或其它可合并优先队列）合并未处理的探测集合E，这样每次合并的复杂度为O(logN+logM)，N次合并的总复杂度为O(NlogN+NlogM)

代码：
Problem : 5575 ( Discover Water Tank ) Judge Status : Accepted
RunId : 15797292 La