SmoothQuant量化介绍

项目链接： GitHub - mit-han-lab/smoothquant: [ICML 2023] SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models

当谈到int8的量化，很多时候失去的（精度）大于收获的（加速效果）

SmoothQuant这种方法，作者声称可以减小int8量化对于精度的损失。

We demonstrate up to 1.56× speedup and 2×memory reduction for LLMs with negligible loss in accuracy.

但是具体怎么实现的呢？

在介绍部分，作者提到LLM太大了，所以我们想通过量化让模型更小，吞吐率更高。之前的方法有提到通过混合精度，来利用fp16表达outlier，但是我咋知道这是离群值呢？所以，不实际！

因此，我们提出了smoothquant（本质上一种per-channel的量化方式）。

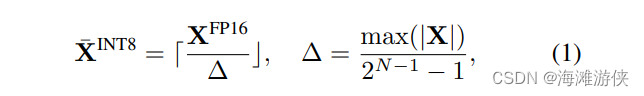
首先，int8量化的方式可以用公式表达，翻译一下找到int8的数值范围，基于权重的最大值，进行一个线性映射。其中，是量化的步长。我们可以离线或者在线的计算，量化的颗粒度也可以有所不同，包括per-tensor， per-token， per-channel， group-wise。

在进行int8量化时，我们希望实现W8A8的量化，也就是权重和激活值都是int8.如果其中一者不是int8，那实际上哦我们并不能利用int型的kernel进行运算。

上面这展厅图解释了per-channel 和per-tensor的量化方式，值得注意的是，per-channel的量化通道还基于outer-loop

LLM的量化难点主要在激活值数值分布不均，outlier甚至有100倍的差别，造成了量化步长被拉伸，而其他激活值输出精度丢失。而权重的分布其实相对较平，甚至可以用int4量化。

但是，这里有个惊人的发现，那就是outlier存在于特定的通道。所以，我们也许可以进行channel-wise的量化。作者在原论文中没有指出这是这是input/output，但是根据语境，大概率是输入的来自同一channel的activation。

针对smoothquant这种方法的理解，我觉得可以分为几个层次，首先从思想层面，它发现了输入的activation具有channel wise的误差，然后，试图把来自activation的误差和量化步长转移一部分到weight中。

从数学层面，论文中的示例图很好的给出了解释， 如果觉得还是不能理解，我写了一段代码便于理解, 与其纠结于理论，不如实践一下。

import numpy as np

#create x w
x =  np.arange(2*4).reshape(2, 4)
w = np.random.rand(4, 3)*4
for i in range(x.shape[0]):
    a[i]*=(i+1)

#calcualte column-wise maximum of x
x_max = np.max(x,axis=0, keepdims=True)

#calculate row-wise maximum of w
w_max = np.max(w,axis=1,keepdims=True)

#key move of smoothquant
xw_norm = np.sqrt(x_max/w_max.T)

sm_result = (x/xw_norm)@(w*xw_norm.T)

print(f"elementwise diff between smoothquant reuslt and original one is {np.mean(sm_result - x@w):.2f}")

小节

smoothquant是一种简洁但是又效果很好的量化方法。作者对于activation和weight的权重分布进行了有效观察，然后提出了这种方法，展现了很强的洞察力。

此外，项目的代码也值得一读。虽然，我目前还没看。。。