单片机ADC采样算法----一阶低通滤波

  关于低通滤波，先看一下百度百科上的定义。

算法实现的公式如下：

 y(n) = q*x(n) + (1-q)*y(n-1)    

其中Y（n）为输出，x（n）为输入，y（n-1）为上一次输出值，其中q为滤波系数。取值范围为0--1.

也就是说若q=0.5时，这个公式代表的意思就是取本次采样值的50%，加上上一次采样值的50%，做为本次的采样结果。也就是说每次的采样结果都和上一次的采样结果相关。

看一下在单片机中C代码的实现

//参数：com 为采样的原始数值
//返回值：iData 经过一阶滤波后的采样值
unsigned int lowV( unsigned int com )
{
    static unsigned int iLastData;    //上一次值
    unsigned int iData;               //本次计算值
    float dPower = 0.1;               //滤波系数
    iData = ( com * dPower ) + ( 1 - dPower ) * iLastData; //计算
    iLastData = iData;                                     //存贮本次数据
    return iData;                                         //返回数据
}

//主函数
void main( void )
{
  while( 1 )
    {
        val1 = ReadVol_CH3() ;         //   读取AD采样值   
        val3 = lowV( val1 );           //   采样值经过一阶滤波算法
        printf("A%d\r\n",val1);        //   打印采样值
        printf("B%d\r\n",val3);        //   打印经过滤波算法后的采样值
    }
}

通过ADC采样输入电压，然后将采样值经过一阶滤波运算，通过串口分别打印采样值和经过一阶滤波运算后的值。

通过串口波形显示软件可以看到采样的结果为：

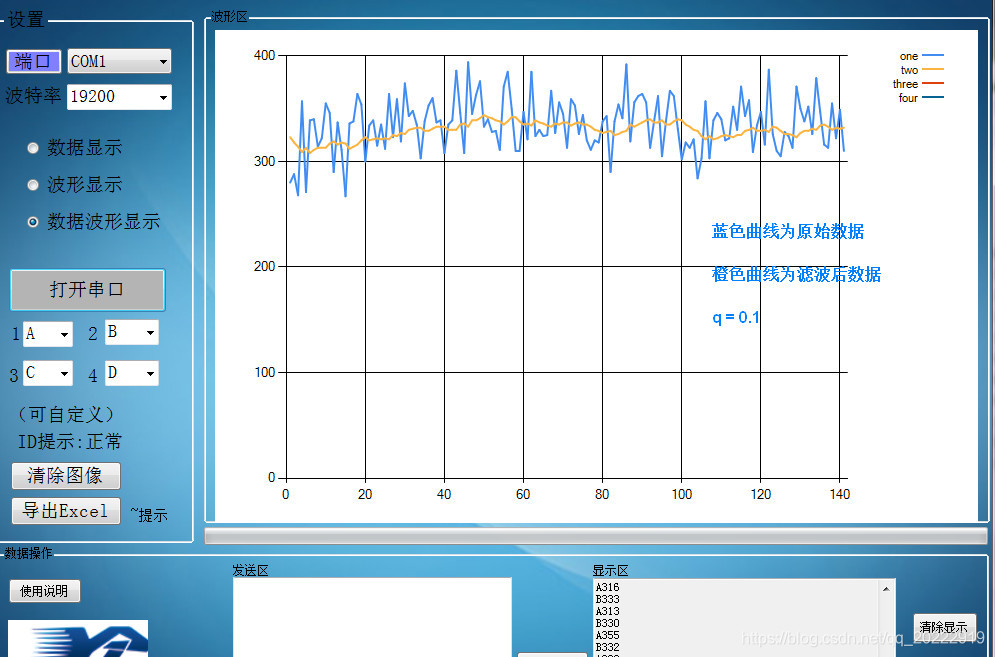
      当滤波系数q=0.1时，本次采样数据占采样结果的10%，上一次采样数据占采样结果的90%，也就是说采样数据突变时对采样结果影响不大，采样的波形比较平滑。

        由上面的波形也可以看出，蓝色波形为原始数据波形，波动范围比较大，橙色波形为经过一阶滤波算法后的波形，波形比较平稳。

  将q值改为0.5时，看看采样情况。

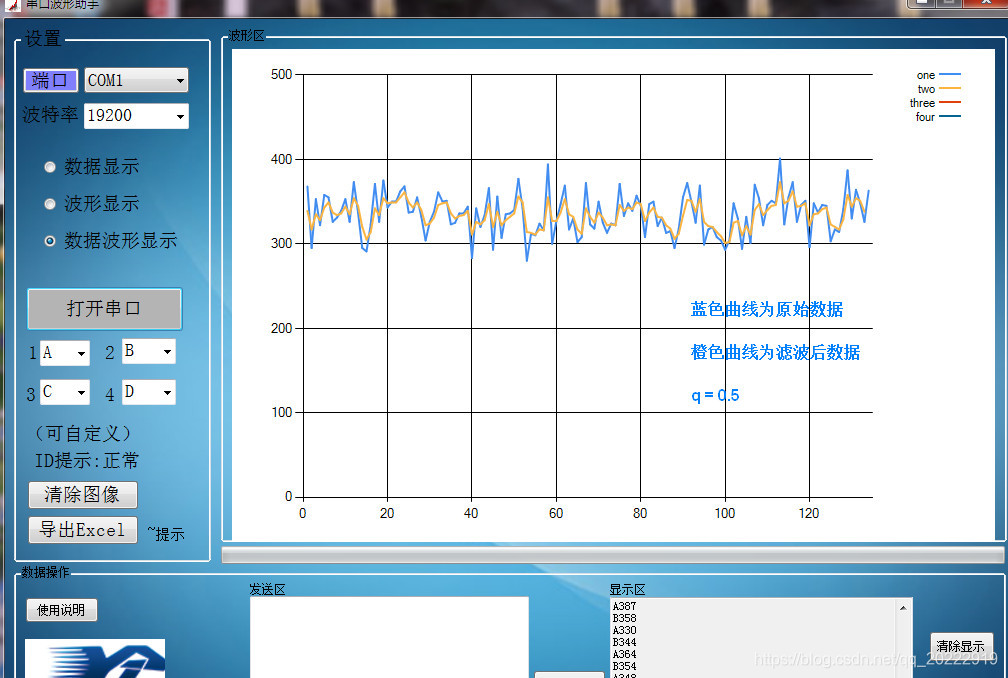
可以看到当滤波系数增大到0.5时，本次采样数据和上次采样数据对结果的影响分别占50%。通过波形可以看到，经过滤波后的波形也出现了波动，但是波动范围相对于原始波形来说小了一点。

将q值继续增大，改为0.9时，看看采样情况。

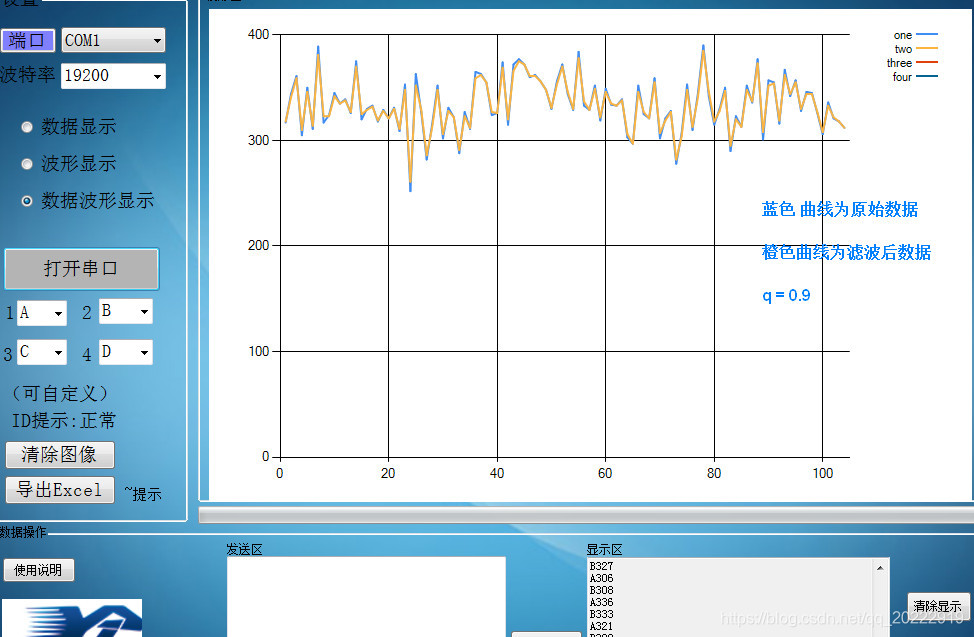
通过波形可以看到将采样系数增大后，本次采样数据对采样结果影响占到了90%，经过一阶滤波后的波形基本和原始波形保持了同步，实时性比较好，但是稳定性会差一点。

通过不同滤波系数的对比发现：

  滤波系数越小，滤波结果越平稳，但是灵敏度越低；

  滤波系数越大，灵敏度越高，但是滤波结果越不稳定。

在实际应用中根据不同的需求，选择合适的滤波系数，以满足系统要求。