深度神经网络基础知识

Contents

• 1 类别不平衡问题
• 2 图像分类
• 3 卷积层神经元连接方式
• 4 双精度、单精度和半精度
• 5 浮点计算能力
• 6 欧式距离
• 7 权重初始化
• 8 激活函数实现去线性化
• 9 分类问题常用损失函数–交叉熵损失
• 10 回归问题常用损失函数–均方误差函数(MSE)
• 11 神经网络优化算法
• 12 学习率的设置-指数衰减法
• 13 过拟合问题
• 14 神经网络权重w的shape
• 15 优化(Optimizers)方法(优化器)
• 16 滑动平均模型
• 17 使用神经网络模型总结
• 18 卷积输出大小计算
• 19 参考资料

导言：在神经网络的架构上，深度学习一方面需要使用激活函数来实现神经网络模型的去线性化，另一方面需要使用一个或 多个隐藏层使得神经网络的结构更深，已解决复杂问题。在训练神经网络时，使用带指数衰减的学习率设置、使用正则化来避免过拟合，以及使用滑动平均模型来使得最终的模型更加健壮。

类别不平衡问题

在很多情况下，可能会遇到数据不平衡问题。数据不平衡是什么意思呢？举一个简单的例子：假设你正在训练一个网络模型，该模型用来预测视频中是否有人持有致命武器。但是训练数据中只有 50 个持有武器的视频，而有 1000 个没有持有武器的视频。如果使用这个数据集完成训练的话，模型肯定倾向于预测视频中没有持有武器。针对这个问题，可以做一些事情来解决：

• 在损失函数中使用权重：对数据量小的类别在损失函数中添加更高的权重，使得对于该特定类别的任何未正确分类将导致损失函数输出非常高的错误。
• 过采样：重复包含代表性不足类别的一些训练实例有助于提升模型精度。
• 欠采样：对数据量大的类别进行采样，降低二者的不平衡程度。
• 数据扩充：对数据量小的类别进行扩充。

图像分类

图像分类顾名思义就是一个模式分类问题，它的目标是将不同的图像，划分到不同的类别，实现最小的分类误差。
1，单标签分类：总体来说，对于单标签的图像分类问题，它可以分为跨物种语义级别的图像分类(cifar10)，子类细粒度图像分类(Caltech-UCSD Birds-200-2011)，以及实例级图像分类(人脸识别)三大类别。

虽然基本的图像分类任务，尤其是比赛趋近饱和，但是现实中的图像任务仍然有很多的困难和挑战。如类别不均衡的分类任务，类内方差非常大的细粒度分类任务，以及包含无穷负样本的分类任务。

2，多标签分类：多标签分类问题，通常有两种解决方案，即转换为多个单标签分类问题，或者直接联合研究。前者，可以训练多个分类器，来判断该维度属性的是否，损失函数常使用 softmax loss。后者，则直接训练一个多标签的分类器，所使用的标签为 0,1,0,0… 这样的向量，使用 hanmming 距离等作为优化目标。

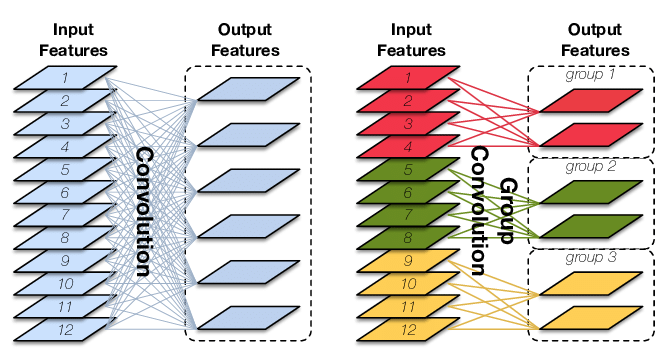
卷积层神经元连接方式

如下图左所示，图片来自链接：

双精度、单精度和半精度

CPU/GPU 的浮点计算能力得区分不同精度的浮点数，分为双精度 FP64、单精度 FP32 和半精度 FP16。因为采用不同位数的浮点数的表达精度不一样，所以造成的计算误差也不一样，对于需要处理的数字范围大而且需要精确计算的科学计算来说，就要求采用双精度浮点数，而对于常见的多媒体和图形处理计算，32 位的单精度浮点计算已经足够了，对于要求精度更低的机器学习等一些应用来说，半精度16位浮点数就可以甚至8位浮点数就已经够用了。
对于浮点计算来说， CPU 可以同时支持不同精度的浮点运算，但在 GPU 里针对单精度和双精度就需要各自独立的计算单元。

浮点计算能力

FLOPS：每秒浮点运算次数，每秒所执行的浮点运算次数，浮点运算包括了所有涉及小数的运算，比整数运算更费时间。下面几个是表示浮点运算能力的单位。

• MFLOPS(megaFLOPS)：等于每秒一佰万(=10^6)次的浮点运算。
• GFLOPS(gigaFLOPS)：等于每秒拾亿(=10^9)次的浮点运算。
• TFLOPS(teraFLOPS)：等于每秒万亿(=10^12)次的浮点运算。
• PFLOPS(petaFLOPS)：等于每秒千万亿(=10^15)次的浮点运算。
• EFLOPS(exaFLOPS)：等于每秒百亿亿(=10^18)次的浮点运算。

欧式距离

欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义，指在 m 维空间中两个点之间的真实距离，或者向量的自然长度(即该点到原点的距离)。在二维和三维空间中的欧氏距离就是两点之间的实际距离。欧式距离公式如下图：

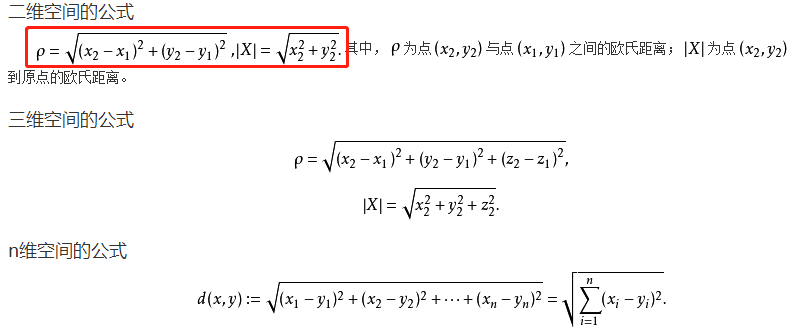
欧式距离公式

权重初始化

权重初始化是一个重要的研究领域。

1，小的随机数：w= 0.01 * np.random.randn(fan_in,fan_out)—-(输入节点数，输出节点数)
2，神经元将饱和，梯度为0：w = 1.0 * np.random.randn(fan_in,fan_out)
3，合理的初始化(Xavier init)：w = np.random.randn((fan_in,fan_out)/np.sqrt(fan_in)

激活函数实现去线性化

如果将每一个神经元(也就是神经网络中的节点)的输出通过一个非线性函数，那么整个神经网络的模型也不再是线性的了。这个非线性函数就是激活函数。常见的几种非线性激活函数如下：

• ReLU函数：\(ReLU(x) = max(x,0)\)
• sigmoid函数：\(\sigma (x) = \frac{1}{1+e(-x)}\)
• tanh函数：\(tanh(x) = 2\sigma(2x) – 1\)

关于损失函数的选择，需要注意，直接优化衡量问题成功的指标不一定总是可行的。有时难以将指标转化为损失函数，要知道，损失函数需要在只有小批量数据时即可计算(理想情况下，只有一个数据点时，损失函数应该也是可计算的)，而且还必须是可微的(否则无法用反向传播来训练网络)。例如，广泛使用的分类指标 ROC AUC 就不能被直接优化。因此在分类任务中，常见的做法是优化 ROC AUC 的替代指标，比如交叉熵。一般来说， 你可以认为交叉熵越小，ROC AUC 越大。下表 4-1 列出了常见问题类型的最后一层激活和损失函数，可以帮你进行选择。

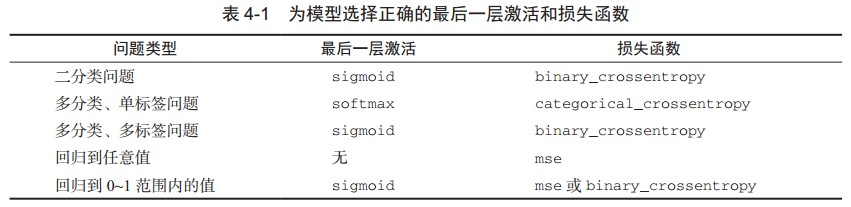
为模型最后一层选择正确的激活函数和损失函数。

分类问题常用损失函数–交叉熵损失

神经网络模型的效果以及优化的目标是通过损失函数(loss function)来定义的。 分类问题和回归问题是监督学习的两大种类。

交叉熵刻画了两个概率分布之间的距离，它是分类问题中使用比较广泛的一种损失函数。给定两个概率分布p和q，通过q来表示p的交叉熵为(p代表正确答案，q代表预测值)：

$$H(p,q)=\sum p(x)logq(x)$$

tensorflow实现交叉熵代码如下：

cross_entroy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y,1e-10,.0))) 

其中 y_ ，代表正确结果，y 代表预测结果。tf.clip_by_value函数可以将一个张量中的数值限制在一个范围之内，这样可以避免一些运算错误(比如log0是无效的)。tf.log函数完成了对张量中所有元素依次求对数的功能。*这个操作不是矩阵乘法，而是元素之间直接相乘。计算张量各个维度上的元素的平均值函数tf.reduce_mean()。
注意交叉熵刻画的是两个概率分布之间的距离。 Softmax回归可以将神经网络的前向传播得到的结果变成概率分布。Softmax回归本身可以作为一个学习算法来优化分类结果。假设原始神经网络的输出为那么经过回归处理后的输出为：\( y_{1},y_{2},…,y_{n-1},y_{n} \),那么经过Softmax回归处理后的输出为：

$$softmax(y)_{i} = y_{i}^{’} = \frac{e^{y_i}}{\sum_{j=1}^{n}e^{y_j}}$$

因为交叉熵一般会与softmax回归一起使用，所以Tensorflow对这两个功能进行统一封装。并提供了tf.nn.softmax_cross_entroy_with_logits函数。TensorFlow实现使用softmax回归之后的交叉熵损失函数代码如下：

cross_entroy = tf..nn.softmax_cross_entroy_with_logits(labels=y_,logits=y)

其中 y 代表了原始神经网络的输出结果，而 y_ 给出了标准答案。

回归问题常用损失函数–均方误差函数(MSE)

与分类问题不同，回归问题解决的是对 具体数值的预测。解决回归问题的神经网络一般只有只有一个输出节点，这个节点的输出值就是预测值。对于回归问题，最常用的损失函数是均方误差(MSE，mean squared error)。(均方误差也是分类问题中常用的一种损失函数)它的定义如下：

$$MSE(y,y_{’}) = \frac{\sum_{i=1}^{n}(y_{i}-y_{i}^{’})^2}{n}$$

其中\(y_{i}\) 为一个batch中的第i个数据的正确答案，而\( y_i^ ′ \)为神经网络给出的预测值。tensorflow实现均方误差函数代码如下：  

mse = tf.reduce_mean(tf.square(y_-y))

这里的减法运算“-”也是两个矩阵中对应元素的减法。

神经网络优化算法

神经网络优化过程可以分为2个阶段，第一个阶段先通过前向传播算法得到预测值，并将预测值和真实值对比得出两者之间的差距。然后在第二个阶段通过反向传播算法计算损失函数对每一个参数的梯度，再根据梯度和学习率使用梯度下降算法更新每一个参数。 

反向传播算法(backpropagation)和梯度下降算法(gradient decent)可以调整神经网络中参数的取值。梯度下降法主要用于优化单个参数的取值，而反向传播算法给出了一个高效的方式在所有参数上使用梯度下降法，从而是神经网络模型在训练数据上的损失函数尽可能小。反向传播算法是训练神经网络的核心算法，它可以根据定义好的损失函数优化神经网络中参数的取值。 

假设用θ表示神经网络参数，J(θ)表示在给定的参数取值下训练数据上损失函数的大小，那么整个优化过程就可以抽象为寻找 一个参数 θ 使得 J(θ) 最小。因为目前没有一个通用的方法可以对任意损失函数直接求解最佳的参数取值，所以在实践中，梯度下降法是最常用的神经网络优化方法。梯度下降法会迭代式更新参数，不断沿着梯度的反方向让参数朝着总损失更小的方向更新。 
通过参数的梯度J(θ)和学习率η，参数更新的公式如下： 

$$\theta_{n+1} = \theta_{n} – \eta\frac{\partial}{\partial\theta_{n}}j(\theta_{n})$$

值得注意的是梯度下降法并不能保证被优化的函数达到全局最优，同时计算时间也太长。现实中综合梯度下降法和随机梯度下降算法的优缺点，采用这两种算法的折中-每次计算一小部分训练数据的损失函数。这小部分数据称为batch。

学习率的设置-指数衰减法

通过指数衰减法设置梯度下降算法中的学习率，通过指数衰减的学习率既可以让模型在训练的前期快速接近最优解，又可以保证模型在训练后期不会有太大的波动，从而更加接近局部最优解。 
tensorflow中使用 tf.train.exponential_decay 函数实现了指数衰减率，代码如下：

leaning_rate = tf.train.exponential_decay(0.1,global_step,100,0.96,staircase=True)
learning_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(my_loss, Global_step=global_step)

上面这段代码设定了初始学习率为 0.1，衰减率为 0.96，global_step为当前迭代轮数，衰减速度为100，因为指定了staircase=True，所以每训练100 轮后学习率便乘以 0.96。一般来说初始学习率、衰减率、衰减速度都是根据经验设置的。

过拟合问题

在训练复杂神经网络模型时，过拟合是一个非常常见的问题。所谓过拟合，指的是当一个模型过于复杂之后，它可以很好的“记忆”每一个训练数据中的随机噪音的部分而忘记了要去“学习”训练数据中的通用趋势。 
为了避免过拟合问题，一个非常有用的方法是正则化(regularization)。正则化的思路就是在损失函数中加入刻画模型复杂度的指标。假设用于刻画模型在训练数据上表现的损失函数为J(θ)，那么在优化时不是直接优化 J(θ) ，而是优化J(θ)+λR(w)。其中R(w)刻画的是模型的复杂度，常用的刻画模型复杂度的函数R(w)有两种，一种是L1正则化，计算公式是: 

$$R(W) = \left \| w \right \|_{1} = \sum_{i}\left | w_{i} \right |$$

另一种是L2正则化，计算公式如下：

$$R(W) = \left \| w \right \|_{2}^{2} = \sum_{i}\left | w_{2}^{2} \right |$$

无论是哪一种正则化，其基本思想都是希望通过限制权重的大小，使得模型不能任意拟合训练数据中随机噪声。L1 与 L2 有很大区别，L1 正则化会让参数变得更加稀疏，而 L2 不会。所谓参数变得更加稀疏是指会有更多的参数变为0，这样可以达到类似 特征选取的功能。下面的代码给出了一个简单的带 L2 正则化的损失函数的定义：

w = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
y = tf.matmul(x,w)
loss = tf.reduce_mean(tf.square(y_-y)+tf.contrib.layers.l2_regularizer(lambda)(w)
# loss为定义的损失函数。tensorflow提供了tf.contrib.layers.l2_regularizer函数，它可以返回一个函数，它可以计算一个给定参数的L2正则化项的值。

神经网络权重w的shape

#生成一个变量
W = tf.get_variable(tf.random_normal(shape),dtype = tf.float32)
# in_dimension为上一层节点数，out_dimension下一层节点数
Shape = [in_dimension,out_dimension)

优化(Optimizers)方法(优化器)

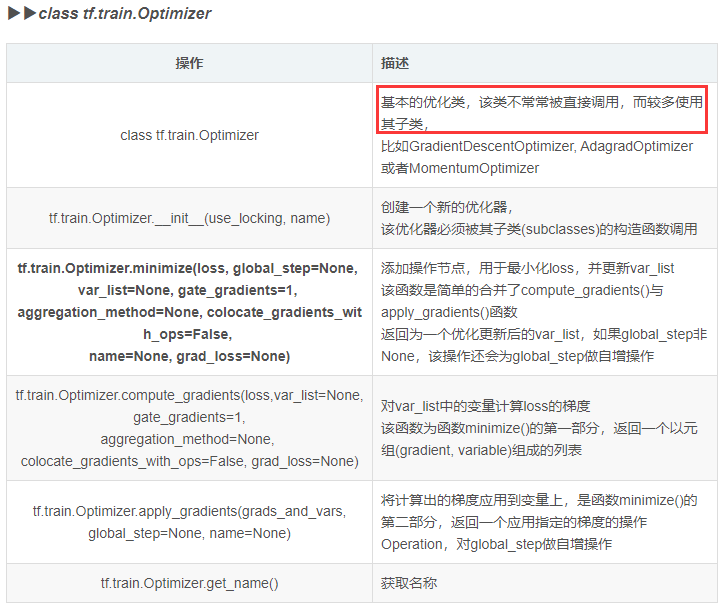
tf中各种优化类提供了为损失函数计算梯度的方法，其中包含比较经典的优化算法，比如GradientDescent、Adagrad和Adam。tensorflow代码如下：

optimizer1 = tf.train.GradientDescentOptimizer.__init__(learning_rate, use_locking=False, name='GradientDescent')
# 使用Adam优化器
optimizer2 = tf.train.AdamOptimizer(learning_rate=learning_rate)

tensorflow1.x常用优化器如下表所示：

滑动平均模型

在采用随机梯度下降算法训练神经网络时，使用滑动平均模型在很多应用中都可在一定程度上提高最终模型在测试数据上的表现。 
原理：在训练神经网络时，不断保持和更新每个参数的滑动平均值，在验证和测试时，参数的值使用其滑动平均值，能有效提高神经网络的准确率。TensorFlow下的 tf.train.ExponentialMovingAverage 需要提供一个衰减率decay。该衰减率用于控制模型更新的速度。该衰减率用于控制模型更新的速度:

$$shadow\_variable = decay*shadow\_variable+(1-decay)*variable$$

ExponentialMovingAverage 对每一个待更新的变量(variable)都会维护一个影子变量(shadow variable)。影子变量的初始值就是这个变量的初始值， 上述公式与之前介绍的一阶滞后滤波法的公式相比较，会发现有很多相似的地方，从名字上面也可以很好的理解这个简约不简单算法的原理：平滑、滤波，即使数据平滑变化，通过调整参数来调整变化的稳定性。 

在滑动平滑模型中， decay 决定了模型更新的速度，越大越趋于稳定。实际运用中，decay 一般会设置为十分接近 1 的常数(0.999或0.9999)。为了使得模型在训练的初始阶段更新得更快，ExponentialMovingAverage 还提供了 num_updates 参数来动态设置 decay 的大小： 

$$decay = min \left \{ decay, \frac{1+num\_updates}{1+num\_updates} \right \}$$

ExponentialMovingAverage类对象部分源代码如下：

def __init__(self, decay, num_updates=None, zero_debias=False,name="ExponentialMovingAverage"):
    """Creates a new ExponentialMovingAverage object.
    The `apply()` method has to be called to create shadow variables and add ops to maintain moving averages.
    The optional `num_updates` parameter allows one to tweak the decay rate dynamically. It is typical to pass the count of training steps, usually kept in a variable that is incremented at each step, in which case the decay rate is lower at the start of training. This makes moving averages
move faster. If passed, the actual decay rate used is:
   `min(decay, (1 + num_updates) / (10 + num_updates))`
    Args:
      decay: Float. The decay to use.
      num_updates: Optional count of number of updates applied to variables.
      zero_debias: If `True`, zero debias moving-averages that are initialized
        with tensors.
      name: String. Optional prefix name to use for the name of ops added in
        `apply()`.
    """
    self._decay = decay
    self._num_updates = num_updates
    self._zero_debias = zero_debias
    self._name = name
    self._averages = {}

使用神经网络模型总结

从神经网络模型结构的设计、损失函数的设计、神经网络模型的优化和神经网络进一步调优4个方面覆盖了设计和优化神经网络过程中可能遇到的主要问题。设计神经网络结构时的两个总体原则–非线性结构和多层结构。

卷积输出大小计算

1. 图片经卷积后输出大小计算公式如下： N = (W − F + 2P )/S+1

• 输入图片大小 W×W
• Filter大小 F×F
• 步长 S
• padding的像素数 P

2. 反卷积得到的图片大小计算方式： 反卷积的大小是由卷积核大小与滑动步长决定， in是输入大小， k是卷积核大小， s是滑动步长， out是输出大小。 
得到 out = (in - 1) * s + k 
例如 输入：2×2， 卷积核：4×4， 滑动步长：3， 输出：7×7 ，其计算过程就是， (2 – 1) * 3 + 4 = 7 

3. 池化得到的特征图大小计算方式： 卷积向下取整，池化向上取整。

参考资料

《tensorflow实战谷歌深度学习框架》
《Python深度学习》【技术综述】你真的了解图像分类吗？