原文地址:https://comzyh.com/blog/archives/492/
给定有向无环图(就是树,不一定有没有根),给定点U,V,找出点R,保证点R是U,V的公共祖先,且深度最深;或者理解为R离这两个点的距离之和最小.如何找出R呢?
最一般的算法是DFS(DFS本是深度优先搜索,在这里姑且把深度优先遍历也叫做DFS,其实是一种不严谨的说法).先看一道赤裸裸的LCA:POJ 1330 Nearest Common Ancestors 这道题给出了根节点,还保证”the first integer is the parent node of the second integer”(输入第一个数是第二个数的祖先),这是赤裸裸的LCA,算法很简单,从根节点DFS一遍,按DFS层数k给每个节点标上深度deep[i]=k.然后从U点DFS到V点,找到后回溯,在回溯的路径上找到一个deep[i]最小的节点即为LCA.
强大的LCA Tarjan算法能在一遍遍历后应答全部的LCA查询,时间复杂的约为Θ(N)
有人说POJ1330是一道LCA Tarjan,在我看来完全不是,LCA Tarjan算法的用途是处理大量请求,如果只有几个(POJ1330每个Case只有一个)询问大可不必写Tarjan算法,不过,1986的编程难度高,如果只是想先学LCA Tarjan, 用1330验证正确性也不是不可以.
LCA Tarjan算法
再来看一道题:POJ1986 Distance Queries 这道题才是真正的LCA Tarjan,只给一个有向无环图,有海量询问;(注意,输入格式与POJ 1984 Navigation Nightmare 一样,需要参考1984的输入格式)
输入格式大意:
第1行:节点数N,边数M
第2…M+1行:起始节点,目标节点,路径长度,方向(无意义字符,本题直接忽略)
第M+2行:询问个数K(1 <= K <= 10,000)
第N+3…2+M+K行:查询 U,V
这道题用DFS做的时间复杂度为Θ(K×N) 显然很不理想,这个时候伟大的Tarjan来了,问题迎刃而解.
首先,LCA Tarjan 是一种离线算法,要求一次读入所有询问,一次性输出,这正是LCA Tarjan 算法的精髓
以下大量引用Sideman神牛的话:
LCA Tarjan基本框架:
先用随便一种数据结构(链表就行),把关于某个点的所有询问标在节点上,保证遍历到一个点,能得到所有有关这个节点LCA 查询
建立并查集.注意:这个并查集只可以把叶子节点并到根节点,即getf(x)得到的总是x的祖先
深度优先遍历整棵树,用一个Visited数组标记遍历过的节点,每遍历到一个节点将Visite[i]设成True 处理关于这个节点(不妨设为A)的询问,若另一节点(设为B)的Visited[B]==True,则回应这个询问,这个询问的结果就是getf(B). 否则什么都不做
当A所有子树都已经遍历过之后,将这个节点用并查集并到他的父节点(其实这一步应该说当叶子节点回溯回来之后将叶子节点并到自己,并DFS另一子树)
当一颗子树遍历完时,这棵子树的内部查询(即LCA在这棵子树内部)都已经处理了
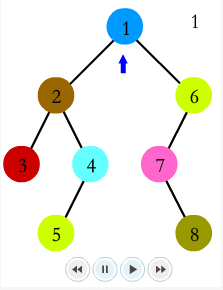
LCA Tarjan 算法演示
假设我们要查询
(3,4) (3,5) (5,6) (6,7) (1,8)
以(3,4)为例,说下Tarjan是如何工作的:
当DFS到3时,发现查询(3,4),查看4是否被DFS过,显然这是不可能的.
回溯到2,将3并入2.
DFS节点4,发现查询(3,4),查看visited[3],发现被访问过,应答查询(3,4),应答getf(3)=2;
LCA Tarjan 算法遍历每个点一遍,处理所有询问,时间复杂度为Θ(N+2M)
下面贴出POJ1986的题解
首先LCA Tarjan 没的说,但是题目要求回应的不是LCA,而是两节点间距离,可以这样做
改造并查集,定义dis[i]数组,保存i到getf(i)的距离
定义Deep[i]数组,表示i节点的深度,DFS时顺便更新depp[i];
定义Sum[I]数组,表示从根节点到I深度节点的距离.因为在LCA Tarjan算法中 ,LCA(设为X) 必然在DFS路径上,所以X到I的距离为sum[deep[I]]-sum[Deep[X]]
响应时,返回值为:dis[A]+sum[deep[getf(A)]]-sum[Deep[B]];
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
#define ll long long
using namespace std;
const int inf=0x3ffffff;
const int MAXN = 40010;
const int MAXM = 100008;
const double eps = 1e-6;
struct Edge{
int next, to, info;
}edge[MAXM];
struct Requst {
int next, to;
}request[MAXM];
int head[MAXN], tot;
int n, m;
int first[MAXN], cnt;
int dis[MAXN];
int father[MAXN], level[MAXN], sum[MAXN];
bool vis[MAXN];
int ans[MAXN];
int find(int x) {
if (x == father[x]) {
return x;
}
int ret = find(father[x]);
dis[x] += dis[father[x]];
return father[x] = ret;
}
void dfs(int x, int dep) {
vis[x] = true;
level[x] = dep;
for (int i = first[x]; i != -1; i = request[i].next) {
if (vis[request[i].to]) {
find(request[i].to);
ans[i/2] = dis[request[i].to] + sum[dep] - sum[level[father[request[i].to]]];
//下标是i/2的原因:在存放请求的时候,是存放两次 其中 i和i|1是一次请求
}
}
for (int i = head[x]; i != -1; i = edge[i].next) {
if (!vis[edge[i].to]) {
sum[dep+1] = sum[dep] + edge[i].info;
dfs(edge[i].to, dep+1);
dis[edge[i].to] = edge[i].info;
father[edge[i].to] = x;
}
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("1.txt", "r", stdin);
#endif
int i, j, k;
int x, y, w;
char c;
while(~scanf("%d%d", &n, &m)) {
tot = 0;
cnt = 0;
memset(vis, false, sizeof(vis));
memset(head, -1, sizeof(head));
memset(first, -1, sizeof(first));
memset(ans, 0, sizeof(ans));
memset(dis, 0, sizeof(dis));
memset(level, 0, sizeof(level));
for (i = 0; i <= n; i++) {
father[i] = i;
}
for (i = 0; i < m; i++) {
scanf("%d %d %d %c", &x, &y, &w, &c);
edge[tot].to = y;
edge[tot].info = w;
edge[tot].next = head[x];
head[x] = tot++;
edge[tot].to = x;
edge[tot].info = w;
edge[tot].next = head[y];
head[y] = tot++;
}
scanf("%d", &k);
for (i = 0; i < k; i++) {
scanf("%d%d", &x, &y);
request[cnt].to = y;
request[cnt].next = first[x];
first[x] = cnt++;
request[cnt].to = x;
request[cnt].next = first[y];
first[y] = cnt++;
}
sum[0] = 0;
dfs(1, 1);
for (i = 0; i < k; i++) {
printf("%d\n", ans[i]);
}
}
return 0;
}























 868
868

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








