数据结构之平衡树(Treap)

平衡树是二叉搜索树和堆合并构成的新数据结构，所以它的名字取了Tree和Heap各一半，叫做Treap。
堆和树的性质是冲突的，二叉搜索树满足左子树<根节点<右子树，而堆是满足根节点小于等于(或大于等于)左右儿子。因此在Treap的数据结构中，并不是以单一的键值作为节点的数据域。

Treap每个节点的数据域包含2个值，key和weight。
key值，和原来的二叉搜索树一样，满足左子树<根节点<右子树。
weight值，随机产生。在Treap中weight值满足堆的性质，根节点的weight值小于等于(或大于等于)左右儿子节点。
比如下图就是一个示例的Treap：

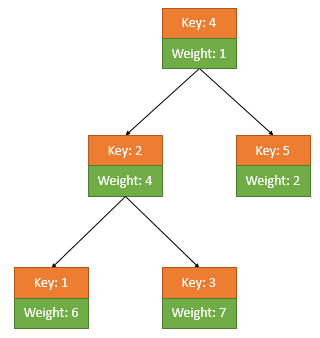
简单理解是话，平衡树就是在二叉搜索树上增加了一个weight值。

因此Treap的大部分操作都和二叉搜索树是一样的，唯一区别在于每次插入一个节点后，需要对树的结构进行调整。

因为每一个节点的weight值不一样，当我们按照key值插入一个节点后，这个节点有可能不满足weight值的要求。

对于如何调整，首先我们来看一个最简单的例子：

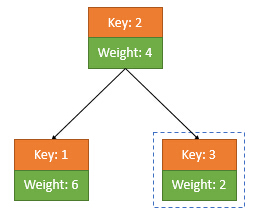
如图所示的一个Treap有三个节点，其中根的右儿子节点是新插入的。

假设我们一开始想要让Treap满足小根堆的性质，即weight值越小越在堆顶。

那么我们需要在不改变key值顺序的情况下，对节点进行变形，使得weight值满足性质。

这一步骤被称为旋转，对于例子，其旋转之后的形态为：

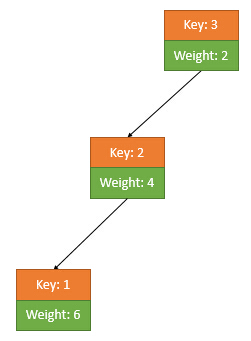
根据旋转的方向不同，旋转分为两种：左旋和右旋。

在例子中是将右儿子节点旋转至根，所以称为左旋。反之将左儿子节点旋转至根，称为右旋。

那么这个旋转具体的过程，我们可以对应旋转前后的图来分析。首先是左旋操作：

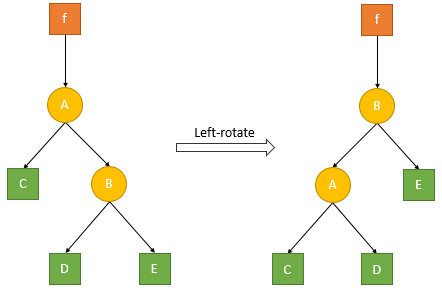
它的过程有如下几步：

1. 获取根节点A的右儿子节点B
2. 将节点B的父亲节点信息更新为f，并更新节点f的子节点信息为B
3. 将节点A的右儿子信息更新为节点B的左儿子D，同时将节点D的父亲节点信息更新为A
4. 将节点B的左儿子信息更改为节点A，同时将节点A的父亲节点信息更改为B

该过程代码如下

void leftRotate(Treap *& a) {
    Treap * b = a->right;
    b->father = a->father;
    if (a->father->left == a){
        a->father->left = b;
    }else {
        a->father->right = b;
    }
    a->right = b->left;
    b->left->father = a;
    b->left = a;
    a->father = b;
}

然后是右旋操作：

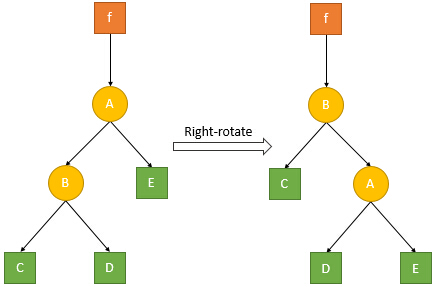
其过程是左旋操作的镜像：

1. 获取根节点A的左儿子节点B
2. 将节点B的父亲节点信息更新为f，并更新节点f的子节点信息为B
3. 将节点A的左儿子信息更新为节点B的右儿子D，同时将节点D的父亲节点信息更新为A
4. 将节点B的右儿子信息更改为节点A，同时将节点A的父亲节点信息更改为B

该过程代码如下

void rightRotate(Treap *& a) {
    Treap * b = a->left;
    b->father = a->father;
    if (a->father->left = a){
        a->father->left = b;
    }else{
        a->father->right = b;
    }
    a->left = b->right;
    b->right->father = a;
    b->right = a;
    a->father = b;
}

只要将节点插入Treap以后，再不断的旋转当前节点直到weight满足堆的性质。

首先我们从插入操作来看，这里我们让insert完成后返回新加入的节点：

Treap* insert(Treap *& p, int key){
    if (p == NULL) { //特殊处理根结点 
        p = new Treap;
        p->left = p->right = NULL;
        p->key = key;
        p->father = NULL;
        p->weight = cnt++;
        return p;
    }
    if (p->key > key){
        if (p->left == NULL){
            p->left = new Treap;
            p->left->left = p->left->right = NULL;
            p->left->key = key;
            p->left->father = p;
            p->left->weight = cnt++;
            return p->left;
        }else{
            return insert(p->left, key);
        }
    }else if (p->key < key){
        if (p->right == NULL){
            p->right = new Treap;
            p->right->left = p->right->right = NULL;
            p->right->key = key;
            p->right->father = p;
            p->right->weight = cnt++;
            return p->right;
        }else{
            return insert(p->right, key);
        }
    }
}

完成插入操作后，我们获得了新加入的节点，然后迭代的进行旋转(这里假设采用小根堆)：

void Rotate(Treap *p) {
    if (p->father != NULL) {
        Treap *fa = p->father;
        if (p->weight < fa->weight){
            if (p = fa->left){
                rightRotate(fa);
            }else{
                leftRotate(fa);
            }
        }
    }
}

另外还有一点，相比较于普通的二叉搜索树，Treap删除节点的操作也有一定的区别。

同样需要根据删除节点的孩子数量来进行处理：

1. 没有孩子节点，则当前结点为叶子节点，直接删去即可。

2. 有一个孩子节点，和普通二叉搜索树相同，让孩子节点代替当前节点。

3. 有两个孩子节点，利用旋转，将weight值小(或大)的子节点旋转到根上，将待删除节点向下旋转。反复操作直到待删除节点只有0个或1个子节点。

Treap * find(Treap* p, int key){
    if (p == NULL){
        return NULL;
    }
    if (p->key == key){
        return p;
    }
    if (p->key > key){
        return find(p->left, key);
    }else{
        return find(p->right, key);
    }
}
void Del(int key) {
    Treap *p = find(root, key);
    Treap *child;
    while(p->left != NULL && p->right != NULL){
        child = p->left;
        if (child->weight > p->right->weight){
            child = p->right;
        }
        if (child == p->left){
            rightRotate(p);
        }else{
            leftRotate(p);
        }
    }
    Treap* fa = p->father;
    if (p->left != NULL){
        p->left->father = fa;
        if (p == fa->left){
            fa->left = p->left;
        }else{
            fa->right = p->left;
        }
    }else if (p->right != NULL){
        p->right->father = fa;
        if (p == fa->left){
            fa->left = p->right;
        }else{
            fa->right = p->right;
        }
    }else{
        if (p == fa->left){
            fa->father = NULL;
        }else{
            fa->right = NULL;
        }
        delete p;
    }
}

对于一般的二叉搜索树，在某些特殊情况下根据输入数据来建树有可能退化为一条链，比如一个依次增大的数列。

而如果一棵二叉排序树的节点是按照随机顺序插入，得到的二叉排序树大多数情况下是平衡的，其期望高度是O(logn)。

因此Treap利用weight值作为随机因子来调整二叉树的形状，使得在大部分情况下比直接通过数据建立的二叉树要平衡。

每一次查找的期望复杂度也会降低，总体的速度也就得到了提高。

hiho一下，第103周代码

#include <iostream>
#include <cstdio> 
#include <algorithm>
using namespace std;
struct Treap{
    int key, weight;
    Treap *left, *right, *father;
}; 
Treap *root = NULL;
int cnt = 0;
void leftRotate(Treap *& a) {
    Treap * b = a->right;
    b->father = a->father;
    if (a->father->left == a){
        a->father->left = b;
    }else {
        a->father->right = b;
    }
    a->right = b->left;
    b->left->father = a;
    b->left = a;
    a->father = b;
}
void rightRotate(Treap *& a) {
    Treap * b = a->left;
    b->father = a->father;
    if (a->father->left = a){
        a->father->left = b;
    }else{
        a->father->right = b;
    }
    a->left = b->right;
    b->right->father = a;
    b->right = a;
    a->father = b;
}
Treap* insert(Treap *& p, int key){
    if (p == NULL) { //特殊处理根结点 
        p = new Treap;
        p->left = p->right = NULL;
        p->key = key;
        p->father = NULL;
        p->weight = cnt++;
        return p;
    }
    if (p->key > key){
        if (p->left == NULL){
            p->left = new Treap;
            p->left->left = p->left->right = NULL;
            p->left->key = key;
            p->left->father = p;
            p->left->weight = cnt++;
            return p->left;
        }else{
            return insert(p->left, key);
        }
    }else if (p->key < key){
        if (p->right == NULL){
            p->right = new Treap;
            p->right->left = p->right->right = NULL;
            p->right->key = key;
            p->right->father = p;
            p->right->weight = cnt++;
            return p->right;
        }else{
            return insert(p->right, key);
        }
    }
}
void Rotate(Treap *p) {
    if (p->father != NULL) {
        Treap *fa = p->father;
        if (p->weight < fa->weight){
            if (p = fa->left){
                rightRotate(fa);
            }else{
                leftRotate(fa);
            }
        }
    }
}
Treap * find(Treap* p, int key){
    if (p == NULL){
        return NULL;
    }
    if (p->key == key){
        return p;
    }
    if (p->key > key){
        return find(p->left, key);
    }else{
        return find(p->right, key);
    }
}
void Del(int key) {
    Treap *p = find(root, key);
    Treap *child;
    while(p->left != NULL && p->right != NULL){
        child = p->left;
        if (child->weight > p->right->weight){
            child = p->right;
        }
        if (child == p->left){
            rightRotate(p);
        }else{
            leftRotate(p);
        }
    }
    Treap* fa = p->father;
    if (p->left != NULL){
        p->left->father = fa;
        if (p == fa->left){
            fa->left = p->left;
        }else{
            fa->right = p->left;
        }
    }else if (p->right != NULL){
        p->right->father = fa;
        if (p == fa->left){
            fa->left = p->right;
        }else{
            fa->right = p->right;
        }
    }else{
        if (p == fa->left){
            fa->father = NULL;
        }else{
            fa->right = NULL;
        }
        delete p;
    }
}
int Query(Treap *p, int key, int last){
    if (p->key > key){
        if (p->left == NULL){
            return last;
        }else{
            return Query(p->left, key, last);
        }
    }else if (p->key < key){
        if (p->right == NULL){
            return p->key;
        }else{
            return Query(p->right, key, max(last, p->key));
        }
    }else{
        return key;
    }
}
int main(){
    int i, j, n, key;
    cin >> n;
    char c;
    root = NULL;
    while(n--){
        cin >> c >> key;
        if (c == 'I'){
            Rotate(insert(root, key));
        }else if (c == 'Q'){
            cout << Query(root, key, -0x3fffffff) << endl;
        }
    }
    return 0;
}