图论：连通分量和强连通分量

1.连通图

1.1 顶点的连通性

在无向图G中，若从顶点vi到顶点vj有路径(当然从vj到vi也一定有路径)，则称vi和vj是连通的。

1.2 连通图

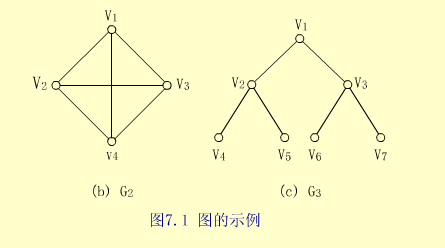
在无向图G中，若V(G)中任意两个不同的顶点vi和vj都连通(即有路径)，则称G为连通图(Con-nected Graph)。【例】图G2，和G3是连通图。

在 有向图 G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点 强连通 (strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个 强连通图 。

2.连通分量

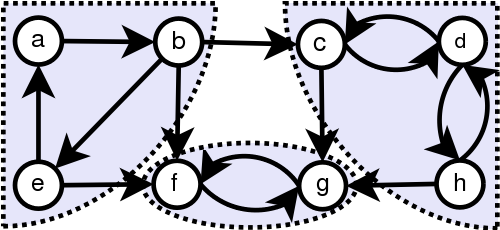
在 图论中 ， 无向图 的 连通分量 （或者仅 分量 ）是一个 子图 ，其中任何两个 顶点 通过 路径 相互 连接 ，并且在 超 图中不连接顶点。例如，图中显示的图形有三个连接的组件。没有边缘的顶点本身就是一个连通的组件。 自身连接的图形只有一个连接组件，由整个图组成。

在有 向图 的数学理论中，如果每个顶点都 可以 从其他顶点 到达 ，则图被称为 强连通 或不 连通 。任意有向图的 强连通分量 或 连通分量 形成一个 划分 成本身强连接的子图。可以 在线性时间内 （即Θ（V + E））测试图的强连通性，或者查找其强连通分量。

2.1.无向图的连通分量

无向图的G的极大连通子图称为G的连通分量（Connected）。任何连通图的连通分量都只有一个，即使是其本身，非连通的无向图有多个连通分量。

使用 广度优先搜索 或 深度优先搜索 来计算线性时间内图的连通分量（以图的顶点和边的数量表示）是很直接的。无论哪种情况，从某个特定顶点 v 开始的搜索将在返回之前找到包含 v （并且不再有）的整个连接组件。要查找图的所有连通分量，循环遍历其顶点，每当循环到达一个尚未包含在先前找到的连通分量中的顶点时，开始新的宽度第一次或深度第一次搜索。

2.1.有向图的强连通分量

有向图强 连通分量 ：在 有向图 G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点 强连通 (strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个 强连通图 。有向图的极大强连通子图，称为强连通 分量 (strongly connected components)。

2.1.1 算法思路

Kosaraju算法思路

这个算法可以说是最容易理解，最通用的算法，其比较关键的部分是同时应用了原图G和反图GT。步骤1：先用对原图G进行深搜形成森林(树)，步骤2：然后任选一棵树对其进行深搜(注意这次深搜节点A能往子节点B走的要求是E-AB存在于反图GT)，能 遍历 到的顶点就是一个强连通分量。余下部分和原来的森林一起组成一个新的森林，继续步骤2直到 没有 顶点 为止。

改进思路：

当然，基本思路实现起来是比较麻烦的(因为步骤2每次对一棵树进行深搜时，可能深搜到其他树上去，这是不允许的，强连通分量只能存在单棵树中(由开篇第一句话可知))，我们当然不这么做，我们可以巧妙的选择第二深搜选择的树的顺序，使其不可能深搜到其他树上去。想象一下，如果步骤2是从森林里选择树，那么哪个树是不连通(对于GT来说)到其他树上的呢？就是最后 遍历 出来的树，它的根节点在步骤1的遍历中离开时间最晚，而且可知它也是该树中离开时间最晚的那个节点。这给我们提供了很好的选择，在第一次深搜遍历时，记录时间i离开的顶点j，即numb[i]=j。那么，我们每次只需找到没有找过的顶点中具有最晚离开时间的顶点直接深搜(对于GT来说)就可以了。每次深搜都得到一个强连通分量。

隐藏性质:

分析到这里，我们已经知道怎么求强连通分量了。但是，大家有没有注意到我们在第二次深搜选择树的顺序有一个特点呢？如果在看上述思路的时候，你的脑子在思考，相信你已经知道了！！！它就是：如果我们把求出来的每个强连通分量收缩成一个点，并且用求出每个强连通分量的顺序来标记收缩后的节点，那么这个顺序其实就是强连通分量收缩成点后形成的 有向无环图 的 拓扑 序列。为什么呢？首先，应该明确搜索后的图一定是有向无环图呢？废话，如果还有环，那么环上的顶点对应的所有原来图上的顶点构成一个强连通分量，而不是构成环上那么多点对应的独自的强连通分量了。然后就是为什么是拓扑序列，我们在改进分析的时候，不是先选的树不会连通到其他树上（对于反图GT来说），也就是后选的树没有连通到先选的树，也即先出现的强连通分量收缩的点只能指向后出现的强连通分量收缩的点。那么 拓扑 序列不是理所当然的吗？这就是 Kosaraju算法 的一个隐藏性质。

伪代码

Kosaraju_Algorithm:

step1：对原图G进行 深度优先遍历 ，记录每个节点的离开时间。

step2：选择具有最晚离开时间的顶点，对反图GT进行 遍历 ，删除能够遍历到的顶点，这些顶点构成一个强连通分量。

step3：如果还有顶点没有删除，继续step2，否则算法结束。

#include<iostream>
#include<cstring>
using namespace std;
const int MAXN=110;
int n;
bool flag[MAXN];//访问标志数组
int belg[MAXN];//存储强连通分量,其中belg[i]表示顶点i属于第belg[i]个强连通分量
int numb[MAXN];//结束时间标记,其中numb[i]表示离开时间为i的顶点
AdjTableadj[MAXN],radj[MAXN];//
邻接表,逆邻接表
//用于第一次深搜,求得numb[1..n]的值
voidVisitOne(int cur,int& sig)
{
    flag[cur]=true;
    for(inti=1;i<=adj[cur][0];++i)
        if(false==flag[adj[cur][i]])
            VisitOne(adj[cur][i],sig);
    numb[++sig]=cur;
}
//用于第二次深搜,求得belg[1..n]的值
voidVisitTwo(int cur,int sig)
{
    flag[cur]=true;
    belg[cur]=sig;
    for(inti=1;i<=radj[cur][0];++i)
        if(false==flag[radj[cur][i]])
            VisitTwo(radj[cur][i],sig);
}
//
Kosaraju算法,返回为强连通分量个数
int Kosaraju_StronglyConnectedComponent()
{
    inti,sig;
    //第一次深搜
    memset(flag+1,0,sizeof(bool)*n);
    for(sig=0,i=1;i<=n;++i)
        if(false==flag[i])
            VisitOne(i,sig);
    //第二次深搜
    memset(flag+1,0,sizeof(bool)*n);
    for(sig=0,i=n;i>0;--i)
        if(false==flag[numb[i]])
            VisitTwo(numb[i],++sig);
    return sig;
}