强化学习导论（Reinforcement Learning: An Introduction）读书笔记(五)：蒙特卡洛方法

感谢 天津包子馅儿的知乎分享。

1. Introduction

1.1 为什么要用MC方法

       ~~~~~~       不同于上一章，在本章中我们不再假设我们对环境有完全的了解（这种情况更加普遍）。相比于其他方式，Monte Carlo 方法不需要完全感知周围的环境，其需要的仅仅是经验 experience，而这些经验既可以是来自真实的场景 actual experience，也可以来自模拟 simulated experience。

1.2 蒙特卡洛方法的特点

       ~~~~~~       在MDP中，我们通过对整个环境的掌握去计算价值函数 value function，而在MC中，我们通过对MPD的抽样数据来计算其价值函数。正如同在DP算法中考虑的那样，我们首先考虑的是在给定策略$\pi$的情况下去计算 $v_{\pi }$以及$q_{\pi }$，之后再对该方法进行提升 (policy improvement）

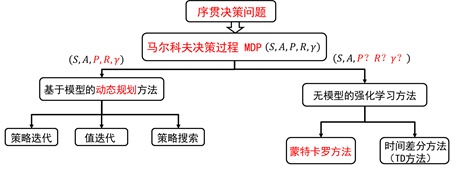
       ~~~~~~        图1为强化学习方法的分类图，如图所示，Monte Carlo方法是一种无模型的强化学习方法。

图1 强化学习方法分类

2. Mote Carlo Prediction

       ~~~~~~       在DP算法中，$v_{\pi }(s)$状态价值函数(state value function)的计算方法如下所示：
$$v_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_{\pi }(s^{\prime })],对所有s\in \mathcal{S}$$
       ~~~~~~       不难得知，在蒙特卡洛方法中，状态转移概率$p(s^{\prime },r|s,a)$是不可知的。在第三章，已经给出状态价值函数的原始的计算方法：
$$v_{\pi }(s)\doteq {\mathbb{E}}_{\pi }\left[G_t|S_t=s\right]={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s\right]，对所有s\in \mathbb{S}$$
       ~~~~~~       该方法仅从数学期望入手，计算状态价值函数(state value function)，蒙特卡洛方式计算数学期望的方式就是通过对状态$s$进行采样，并对采样的$G_t$求均值，所得到的结果就是$s$的状态价值函数。

2.1 first-vist MC 与 every-visit MC

       ~~~~~~       我们必须考虑一种情况，那就是在每次实验 episode 中，状态$s_t$可能会被多次访问。
       ~~~~~~       针对第一次的访问，我们称之为：first visit to s
       ~~~~~~       因此，针对状态$s$，我们有两种方式来计算$v_{\pi }(s)$，分别为：

• first-visit MC method : 在一次实验中，仅仅返回第一次访问的 $G$ 值。
• every-visit MC method : 在一次实验中，返回每次访问的 $G$ 值。

图2 first-visit MC Prediction

       ~~~~~~       而由大数定律可知：无论是哪种访问方式，当样本接近无限时，其都会收敛到$v_{\pi }(s)$，

2.2 游戏21点

       ~~~~~~       蒙特卡洛方法的应用在赌博游戏中最为常见。其中一个常见的例子就是游戏21点。其规则如下：

庄家给每个玩家发两张明牌，牌面朝上面；给自己发两张牌，一张牌面朝上(叫明牌)，一张牌面朝下(叫暗牌)。大家手中扑克点数的计算是：K、Q、J 和 10 牌都算作 10 点。 A 牌既可算作1 点也可算作11 点，由玩家自己决定。其余所有2 至9 牌均按其原面值计算。首先玩家开始要牌，如果玩家拿到的前两张牌是一张 A 和一张10点牌，就拥有黑杰克(Blackjack)；此时，如果庄家没有黑杰克，玩家就能赢得2倍的赌金（1赔2）。如果庄家的明牌有一张A，则玩家可以考虑买不买保险，金额是赌筹的一半。如果庄家是blackjack，那么玩家拿回保险金并且直接获胜；如果庄家没有blackjack则玩家输掉保险继续游戏。没有黑杰克的玩家可以继续拿牌，可以随意要多少张。目的是尽量往21点靠，靠得越近越好，最好就是21点了。在要牌的过程中，如果所有的牌加起来超过21点，玩家就输了——叫爆掉(Bust)，游戏也就结束了。假如玩家没爆掉，又决定不再要牌了，这时庄家就把他的那张暗牌打开来。假如庄家爆掉了，那他就输了。假如他没爆掉，那么你就与他比点数大小，大为赢。一样的点数为平手，你可以把你的赌注拿回来。

动作(action): 21点游戏中，玩家的动作有两个，{hit，stick}
状态(state): 该游戏的状态就是手中牌的点数以及庄家的明牌点数。
奖励(reward): 若玩家胜利，奖励为+1，若失败，奖励为-1，平局奖励为0。

       ~~~~~~       在这种条件下，状态转移函数$p(s^{{}^{\prime }},r|s,a)$难以确定，采用蒙特卡洛产生样本估计价值函数的难度就大大下降。

2.3 备份图的对比

       ~~~~~~       在备份图上，蒙特卡洛方法与传统的DP方法相比有较大的不同。

图3 蒙特卡洛方法的备份图

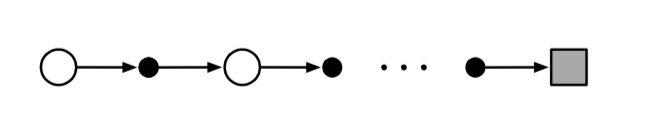
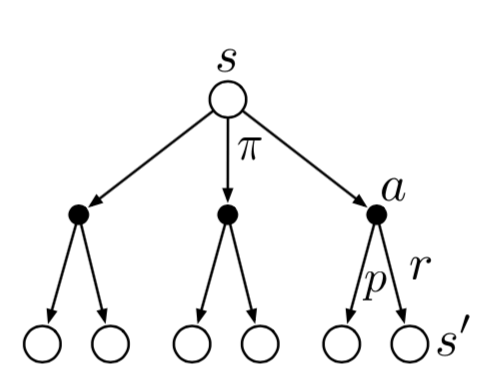
       ~~~~~~       图3所展示的是某次实验中蒙特卡洛方法的备份图。在一个episode中，蒙特卡洛方法所选择的状态以及动作都是唯一的。这不同于图4所展示的DP算法的备份图。其展示了所有可能的状态转移过程。

图4 DP算法的备份图

     ~~~~     综上，蒙特卡洛方法的三个优势在于

• learn from actual experience.
• learn from simulated experience
• One can generate many sample episodes starting from the states of interest (可以单独考虑你感兴趣的那块内容)

3. Monte Carlo Estimation of Action Value

       ~~~~~~       传统的DP方式求得 状态-价值函数(state-value function) 就可以制定策略。在蒙特卡洛方法中，我们对模型是未知的，更好的办法是计算 动作价值函数(action-value function)$q_{\pi }(s,a)$,在知道了动作价值后，对策略提升的作用更加直观。

3.1 存在的问题

       ~~~~~~       该方法中存在的最大的问题是在给定策略$\pi$的情况下，并不是所有的动作都会被选中。如果一个动作无法被选中，那么评估其价值更是无稽之谈。
       ~~~~~~       在非探索开端的蒙特卡洛方法中(Monte Carlo Control without Exploring Starts)，共有两种解决思路。分别被称为：

• on-policy: 在同一个策略中进行策略评估以及策略提升。
• off-policy在不同的策略中进行策略评估与策略提升。

3.2 start in a state-action pair

        ~~~~~~~        该问题的其中一个解决办法就是使用 “start in a state-action pair”，即在开始时选择特定的state-value piar

3.3 $ϵ$ - greedy method

       ~~~~~~       $ϵ$ - greedy method 借助的是第二章中的算法。其原理就是在状态$s$中以$1-ϵ$的概率选择回报最大的动作，以$ϵ$的概率选择其他动作。

4. Monte Carlo Control

        ~~~~~~~        蒙特卡洛版本的(policy iteration)也遵从同一个方案，即反复使用策略提升以及策略估计。具体的迭代过程如下所示：
$${\pi }_0\stackrel{E}{\to }{q}_{{\pi }_0}\stackrel{I}{\to }{\pi }_1\stackrel{E}{\to }{q}_{{\pi }_1}\stackrel{I}{\to }{\pi }_2\stackrel{E}{\to }\cdots \stackrel{I}{\to }{\pi }_{\ast }\stackrel{E}{\to }{q}_{\ast }$$
       ~~~~~~       以任意的策略为起始点，经过策略评估与策略提升，可以得到最优策略。

4.1 策略提升

       ~~~~~~        策略提升的过程与DP算法的一致，即使用贪心策略：在每个状态下都选择最优动作：(这里的前提就需要将所有的动作的价值都计算一遍，即 start in a state-action pair)
$$\pi (s)\dot{=}arg\underset{a}{\max }q(s,a)$$
       ~~~~~~       只要保证提升后的策略都比提升前的好，那么整个策略会一直向最优策略靠近。

4.2 remove infinite number of episodes

       ~~~~~~       为了完全评估某个策略，理论上需要的实验数量是无穷的。但是在实际情况中，无穷次实验明显是不现实的。第一种解决方法是借助DP算法中的方法，仅仅评估 (state-value) $q_{{\pi }_k}$的近似值，避免无穷次实验。
       ~~~~~~       第二种解决办法是模仿上章的价值迭代 (value iteration) ，在价值评估没有完全完成的情况下进行价值迭代，理论上这也是可行的。相比于价值迭代，状态的价值每更新一次就进行一次策略提升。在蒙特卡洛方法中，比较自然的方式就是每进行一次实验，就进行一次策略提升。
       ~~~~~~       这种方法我们称为 Monte Carlo ES(Exploring Starts) 其算法图如下所示：

图5 Monte Carlo ES(Exploring Starts)

5. Monte Carlo Control without Exploring Starts

5.1 On-policy method

       ~~~~~~       On-policy method是将产生样本数据的策略与进行策略提升和策略评价的策略放在一起。上文中的 start in a state-action pair 就是一种On-policy method。
       ~~~~~~       在采用On-policy method时，确保采用的策略是 soft，其确保每个动作都会被选择。
       ~~~~~~       在使用$ϵ-greedy$算法的条件下，所有的非贪心的动作被选则的概率为：$\frac{ϵ}{|\mathcal{A}(s)|}$，而剩下的贪心动作被选中的概率为：$1-ϵ+\frac{ϵ}{|\mathcal{A}(s)|}$，在这样的策略下，我们不能保证策略一直是贪心的，但是策略仍然向最优策略靠近。
       ~~~~~~       在使用 (first-visit MC) 的基础下，该策略的算法过程如下：

图6 On-policy first-visit MC control

5.2 Off-policy Prediction

       ~~~~~~       Off-policy method被称为异策略，即使用两种策略，一种是 behavior policy 用来产生数据，另一种是 target policy ,用来做策略评估以及提升。
       ~~~~~~       想要让两种策略产生联系，需要的方法为 importance sampling 。

5.2.1ordinary importance sampling

给定一个初始状态$S_t$,在策略$\pi$前提下，其状态动作变化的轨迹为：$A_t,S_{t+1},A_{t+1},\dots ,S_T$的概率为：
P r { A t , S t + 1 , A t + 1 , … , S T ∣ S t , A t : T − 1 ∼ π } = π ( A t ∣ S t ) p ( S t + 1 ∣ S t , A t ) π ( A t + 1 ∣ S t + 1 ) ⋯ p ( S T ∣ S T − 1 , A T − 1 ) = ∏ k = t T − 1 π ( A k ∣ S k ) p ( S k + 1 ∣ S k , A k ) , \begin{aligned} &Pr\{A_t, S_{t+1},A_{t+1},\dots,S_T | S_t,A_{t:T-1} \sim \pi\} \\ &=\pi(A_t|S_t)p(S_{t+1}|S_t,A_t)\pi(A_{t+1}|S_{t+1})\cdots p(S_{T}|S_{T-1},A_{T-1}) \\ &=\prod_{k=t}^{T-1} \pi(A_k|S_k)p(S_{k+1}|S_k,A_k), \end{aligned} ​Pr{At​,St+1​,At+1​,…,ST​∣St​,At:T−1​∼π}=π(At​∣St​)p(St+1​∣St​,At​)π(At+1​∣St+1​)⋯p(ST​∣ST−1​,AT−1​)=k=t∏T−1​π(Ak​∣Sk​)p(Sk+1​∣Sk​,Ak​),​
同理，在策略$b$下，相同的动作状态发生的概率为：
$$\prod _{k=t}^{T-1}b(A_k|S_k)p(S_{k+1}|S_k,A_k)$$
那么，相对概率 (the importance-sampling ration) 是：
$${\rho }_{t:T-1}\doteq \frac{{\prod }_{k=t}^{T-1}\pi (A_k|S_k)p(S_{k+1}|S_k,A_k)}{{\prod }_{k=t}^{T-1}b(A_k|S_k)p(S_{k+1}|S_k,A_k)}=\prod _{k=t}^{T-1}\frac{\pi (A_k|S_k)}{b(A_k|S_k)}\text{\hspace{1em}(5.3)}$$
由上述式子可知，由于状态转移概率是给定的，所以最后的比率仅仅和两个策略相关。
状态价值评估的方式：
       ~~~~~~       将所有的实验的步数$t$连起来，假设第一次实验的最后一步是100，那么下一个实验的第一步就是101。我们在这里采用 first-visit ，记录每次被访问到的$s$，用 $\mathcal{T}(s)$表示。$T(t)$代表了距离步骤$t$最近的终止步骤。$G_t$代表了从$t$开始到$T(t)$的回报， { G t } t ∈ T ( s ) \{G_t\}_{t \in \mathcal{T}(s)} {Gt​}t∈T(s)​ 代表了状态$s$的所有回报的集合， { ρ t : T ( t ) − 1 } t ∈ T ( s ) \{\rho_{t:T(t)-1} \}_{t \in \mathcal{T}(s)} {ρt:T(t)−1​}t∈T(s)​表示对应的重要性采样率
$$V(s)\doteq \frac{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}{G}_t}{|\mathcal{T}(s)|}.$$
       ~~~~~~       该方法被称为原始重要性采样ordinary importance sampling

5.2.2 weighted importance samping

       ~~~~~~       另外一种评价方式就是对分母进行加权，该方式称为$weightedimportancesamping$:
$$V(s)\doteq \frac{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}{G}_t}{{\sum }_{t\in \mathcal{T}(s)}{\rho }_{t:T(t)-1}}$$

5.2.3 不同之处

       ~~~~~~       两种方式最大的不同之处在于他们的偏差biase和方差variance，weighted importance samping是有偏差的，虽然偏差会逐渐变为0。在ordinary importance sampling中，方差值可能会接近无穷，因为相对概率就可能是没有边界的，在weighted importance samping中，方差就是1。

5.2.4 ordinary importance sampling中对方差的计算

       ~~~~~~       如下图所示，假设有这样一种情况。在状态$s$下，只存在两种动作选择，{left, right}，right动作会使得状态移动到termination,奖励为0。left动作会有0.9的概率转变为原始的状态，奖励为0，同时有0.1的概率变为termination,奖励为1。

图7 infinte variance sample

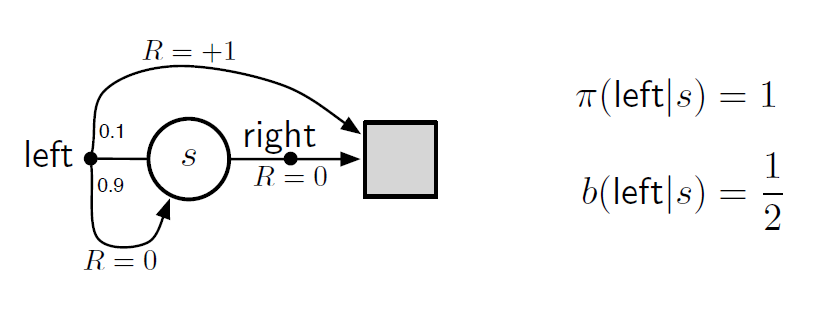
       ~~~~~~       通过重要信息采集ordinary importance sampling得到的样本的均值作为状态$s$的价值函数，那么其方差是什么呢？
       ~~~~~~       方差的计算方法如下：
$$Var[X]\doteq \mathbb{E}[(X-\overline{X}{)}^2]=\mathbb{E}[X^2-2X{\overline{X}}^2+{\overline{X}}^2]=\mathbb{E}[X^2]-{\overline{X}}^2.$$
       ~~~~~~       显然，${\overline{X}}^2$肯定不是一个会无穷大的数，那么一定是$\mathbb{E}[X^2]$的值为无穷。这里的$X$是重要采样方法得到的样本。根据期望的计算公式，我们需要求得每种样本发生的概率以及样本本身的值。
$${\mathbb{E}}_b\left[{\left(\prod _{t=0}^{T-1}\frac{\pi (A_t|S_t)}{b(A_t|S_t)}{G}_0\right)}^2\right]$$
      ~~~~~      这里$G_0$为1,可以省略，$\frac{\pi (A_t|S_t)}{b(A_t|S_t)}$只包括了$b$中所有只选择left的动作(因为策略$\pi$是没有right动作的)。计算上述例子的方差：

图8 重要采样样本的方差计算

6. Incremental Implementation

       ~~~~~~       如第二章，同样可以使用蒙特卡洛的增量方法。对于给定的回报序列$G_1,G_2,\dots ,G_{n-1}$，其权重设置为$W_i$($W_i={\rho }_{t_i:T(t_i)-1}$)，对于单次实验中的每一个step，价值估计为:
$$V_n\doteq \frac{{\sum }_{k=1}^{n-1}{W}_k{G}_k}{{\sum }_{k=1}^{n-1}{W}_k},n\ge 2$$
       ~~~~~~       若得到一个新的$G_n$以及$W_n$，状态价值的迭代函数为：
$$V_{n+1}\doteq V_n+\frac{W_n}{C_n}\left[G_n-V_n\right],n\ge 1$$
       ~~~~~~       其中：
$$C_{n+1}\doteq C_n+W_{n+1}$$
       ~~~~~~       其中，$G_0=0$，同时$V_1$是随机的。具体的算法如下所示：

图9 增量法实现异策略

7 Off-policy Monte Carlo Control

        ~~~~~~~        在借助GPI以及wighted importance sampling的条件下，Off-policy Monte Carlo Control method如下所示：

图10 Off-policy Monte Carlo Control