引言:为什么动态规划如此重要?
动态规划(Dynamic Programming,简称DP)是计算机科学中最重要的算法思想之一,也是技术面试中的高频考点。根据LeetCode的统计,动态规划类题目在各大公司的面试中出现频率高达25%以上,尤其是在Facebook、Google、Amazon等顶级科技公司的面试中。
动态规划的魅力在于它能够将指数级别时间复杂度的问题优化到多项式级别,这种"化腐朽为神奇"的能力使其成为解决复杂优化问题的利器。本文将深入探讨动态规划的核心思想、常见模型、优化技巧,并通过详细的Java代码实现帮助读者彻底掌握这一重要算法。
第一章:动态规划基础理论
1.1 什么是动态规划?
动态规划是一种通过将复杂问题分解为相互重叠的子问题,并存储子问题的解以避免重复计算的方法论。
它的核心思想可以概括为:"记住过去,优化未来"。
与分治算法类似,动态规划也采用分而治之的策略,但关键区别在于:
-
分治法的子问题通常是独立的
-
动态规划的子问题是重叠的,需要记忆化存储
1.2 动态规划的适用条件
一个问题适合用动态规划解决,必须满足两个基本条件:
1.2.1 最优子结构(Optimal Substructure)
问题的最优解包含其子问题的最优解。这意味着我们可以通过子问题的最优解来构造原问题的最优解。
数学表达:
如果问题P可以分解为子问题P₁, P₂, ..., Pₖ,且P的最优解可以由P₁, P₂, ..., Pₖ的最优解组合得到,那么P就具有最优子结构。
1.2.2 重叠子问题(Overlapping Subproblems)
在递归求解过程中,相同的子问题会被多次重复计算。动态规划通过记忆化存储来避免这种重复计算。
1.3 动态规划的两种实现方式
1.3.1 自顶向下(Top-Down) - 记忆化搜索
// 伪代码示例
Map<State, Result> memo = new HashMap<>();
Result solve(Problem problem) {
if (isBaseCase(problem)) {
return baseSolution(problem);
}
if (memo.containsKey(problem)) {
return memo.get(problem);
}
Result result = combine(solve(subProblem1), solve(subProblem2), ...);
memo.put(problem, result);
return result;
}
1.3.2 自底向上(Bottom-Up) - 迭代填表
// 伪代码示例
Result[] dp = new Result[n + 1];
// 初始化基础情况
dp[0] = baseCase0;
dp[1] = baseCase1;
for (int i = 2; i <= n; i++) {
dp[i] = combine(dp[i - 1], dp[i - 2], ...);
}
return dp[n];
两种方法的对比:
-
自顶向下:思路直观,易于理解,但递归有栈溢出风险
-
自底向上:效率更高,避免递归开销,但需要确定计算顺序
第二章:动态规划解题框架
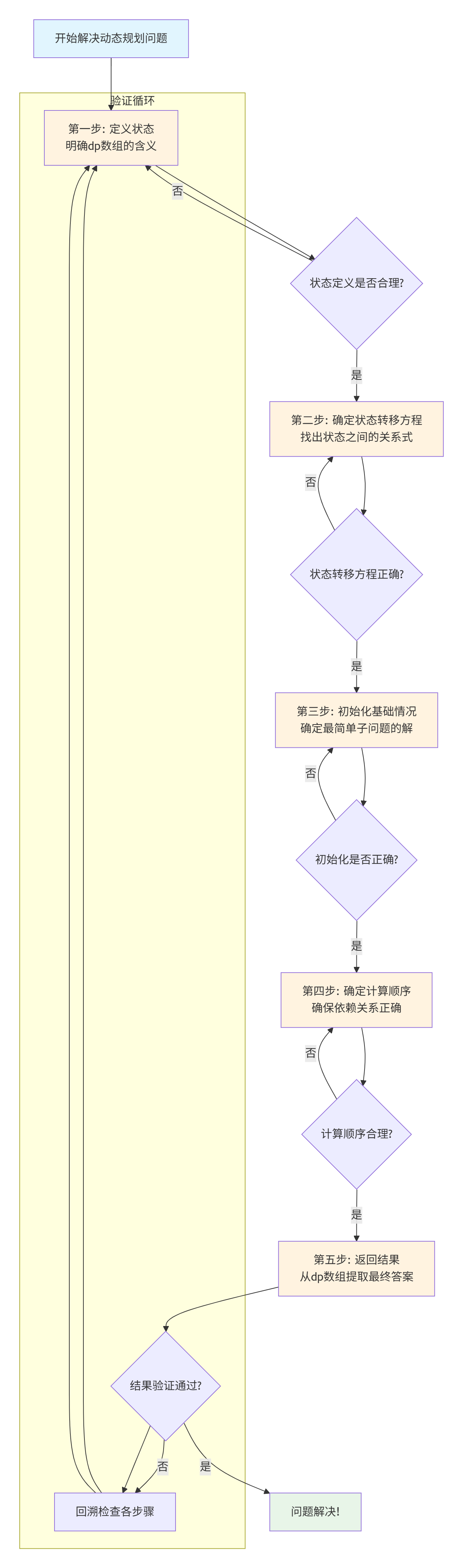
2.1 五步解题法
-
定义状态:明确dp数组的含义
-
确定状态转移方程:找出状态之间的关系
-
初始化基础情况:确定最简单子问题的解
-
确定计算顺序:确保依赖关系正确
-
返回结果:从dp数组提取最终答案
2.2 状态定义技巧
状态定义是动态规划中最关键的一步,常见模式包括:
-
线性DP:dp[i] 表示前i个元素的最优解
-
区间DP:dp[i][j] 表示区间[i, j]的最优解
-
状态机DP:dp[i][state] 表示第i步处于某种状态时的最优解
-
背包DP:dp[i][w] 表示前i个物品在容量w下的最优解
第三章:经典动态规划问题详解
3.1 斐波那契数列
这是最经典的动态规划入门问题,完美展示了重叠子问题的特性。
问题描述:F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2)
3.1.1 基础版本
public class Fibonacci {
// 基础递归版本 - 时间复杂度O(2^n)
public static int fibRecursive(int n) {
if (n <= 1) return n;
return fibRecursive(n - 1) + fibRecursive(n - 2);
}
// 记忆化搜索版本 - 时间复杂度O(n)
public static int fibMemo(int n) {
if (n <= 1) return n;
int[] memo = new int[n + 1];
Arrays.fill(memo, -1);
memo[0] = 0;
memo[1] = 1;
return fibHelper(n, memo);
}
private static int fibHelper(int n, int[] memo) {
if (memo[n] != -1) return memo[n];
memo[n] = fibHelper(n - 1, memo) + fibHelper(n - 2, memo);
return memo[n];
}
// 迭代动态规划版本 - 时间复杂度O(n),空间复杂度O(n)
public static int fibDP(int n) {
if (n <= 1) return n;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
// 空间优化版本 - 空间复杂度O(1)
public static int fibOptimized(int n) {
if (n <= 1) return n;
int prev = 0, curr = 1;
for (int i = 2; i <= n; i++) {
int next = prev + curr;
prev = curr;
curr = next;
}
return curr;
}
}
3.1.2 矩阵快速幂优化
对于斐波那契数列,还可以使用矩阵快速幂将时间复杂度优化到O(log n):
public class FibonacciMatrix {
// 矩阵快速幂方法 - 时间复杂度O(log n)
public static int fibMatrix(int n) {
if (n <= 1) return n;
int[][] matrix = {{1, 1}, {1, 0}};
int[][] result = matrixPower(matrix, n - 1);
return result[0][0];
}
// 矩阵幂运算
private static int[][] matrixPower(int[][] matrix, int power) {
int[][] result = {{1, 0}, {0, 1}}; // 单位矩阵
while (power > 0) {
if (power % 2 == 1) {
result = multiplyMatrix(result, matrix);
}
matrix = multiplyMatrix(matrix, matrix);
power /= 2;
}
return result;
}
// 矩阵乘法
private static int[][] multiplyMatrix(int[][] a, int[][] b) {
int[][] result = new int[2][2];
result[0][0] = a[0][0] * b[0][0] + a[0][1] * b[1][0];
result[0][1] = a[0][0] * b[0][1] + a[0][1] * b[1][1];
result[1][0] = a[1][0] * b[0][0] + a[1][1] * b[1][0];
result[1][1] = a[1][0] * b[0][1] + a[1][1] * b[1][1];
return result;
}
}
3.2 爬楼梯问题
问题描述:假设你正在爬楼梯,需要n阶才能到达楼顶。每次你可以爬1或2个台阶。有多少种不同的方法可以爬到楼顶?
分析:这本质上就是斐波那契数列问题,因为到达第n阶的方法数等于到达第n-1阶和第n-2阶的方法数之和。
public class ClimbingStairs {
// 基础动态规划解法
public static int climbStairs(int n) {
if (n <= 2) return n;
int[] dp = new int[n + 1];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
// 空间优化版本
public static int climbStairsOptimized(int n) {
if (n <= 2) return n;
int prev = 1, curr = 2;
for (int i = 3; i <= n; i++) {
int next = prev + curr;
prev = curr;
curr = next;
}
return curr;
}
// 扩展:如果每次可以爬1、2或3个台阶
public static int climbStairsThree(int n) {
if (n <= 2) return n;
if (n == 3) return 4;
int a = 1, b = 2, c = 4;
for (int i = 4; i <= n; i++) {
int d = a + b + c;
a = b;
b = c;
c = d;
}
return c;
}
// 扩展:带有成本的最小爬楼梯
public static int minCostClimbingStairs(int[] cost) {
int n = cost.length;
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 0;
for (int i = 2; i <= n; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[n];
}
}
3.3 背包问题系列
背包问题是动态规划的经典应用,有多种变体。
3.3.1 0-1背包问题
问题描述:给定一组物品,每个物品有重量weight和价值value,在限定的总容量capacity内,如何选择物品使得总价值最大。
public class Knapsack {
// 二维DP解法
public static int knapsack01(int[] weights, int[] values, int capacity) {
int n = weights.length;
// dp[i][w] 表示前i个物品在容量w下的最大价值
int[][] dp = new int[n + 1][capacity + 1];
for (int i = 1; i <= n; i++) {
for (int w = 1; w <= capacity; w++) {
if (weights[i - 1] <= w) {
// 选择当前物品或不选择
dp[i][w] = Math.max(
dp[i - 1][w],
dp[i - 1][w - weights[i - 1]] + values[i - 1]
);
} else {
dp[i][w] = dp[i - 1][w];
}
}
}
return dp[n][capacity];
}
// 空间优化版本 - 一维数组
public static int knapsack01Optimized(int[] weights, int[] values, int capacity) {
int n = weights.length;
int[] dp = new int[capacity + 1];
for (int i = 0; i < n; i++) {
// 逆序遍历避免重复计算
for (int w = capacity; w >= weights[i]; w--) {
dp[w] = Math.max(dp[w], dp[w - weights[i]] + values[i]);
}
}
return dp[capacity];
}
// 输出具体选择的物品
public static List<Integer> knapsackWithPath(int[] weights, int[] values, int capacity) {
int n = weights.length;
int[][] dp = new int[n + 1][capacity + 1];
// 记录选择路径
boolean[][] chosen = new boolean[n + 1][capacity + 1];
for (int i = 1; i <= n; i++) {
for (int w = 1; w <= capacity; w++) {
if (weights[i - 1] <= w) {
int notTake = dp[i - 1][w];
int take = dp[i - 1][w - weights[i - 1]] + values[i - 1];
if (take > notTake) {
dp[i][w] = take;
chosen[i][w] = true;
} else {
dp[i][w] = notTake;
}
} else {
dp[i][w] = dp[i - 1][w];
}
}
}
// 回溯找出选择的物品
List<Integer> result = new ArrayList<>();
int w = capacity;
for (int i = n; i >= 1; i--) {
if (chosen[i][w]) {
result.add(i - 1); // 添加物品索引
w -= weights[i - 1];
}
}
Collections.reverse(result);
return result;
}
}
3.3.2 完全背包问题
问题描述:与0-1背包不同,每种物品可以选择无限次。
public class CompleteKnapsack {
// 完全背包解法
public static int completeKnapsack(int[] weights, int[] values, int capacity) {
int n = weights.length;
int[] dp = new int[capacity + 1];
for (int i = 0; i < n; i++) {
// 正序遍历,允许重复选择
for (int w = weights[i]; w <= capacity; w++) {
dp[w] = Math.max(dp[w], dp[w - weights[i]] + values[i]);
}
}
return dp[capacity];
}
// 零钱兑换问题 - 求最少硬币数
public static int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1); // 初始化为最大值
dp[0] = 0;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
// 零钱兑换问题 - 求组合数
public static int coinChangeCombinations(int[] coins, int amount) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i - coin];
}
}
return dp[amount];
}
}
3.3.3 多重背包问题
问题描述:每种物品有数量限制,既不是无限也不是只有一个。
public class MultipleKnapsack {
// 多重背包基础解法
public static int multipleKnapsack(int[] weights, int[] values, int[] counts, int capacity) {
int n = weights.length;
int[] dp = new int[capacity + 1];
for (int i = 0; i < n; i++) {
for (int w = capacity; w >= weights[i]; w--) {
for (int k = 1; k <= counts[i] && k * weights[i] <= w; k++) {
dp[w] = Math.max(dp[w], dp[w - k * weights[i]] + k * values[i]);
}
}
}
return dp[capacity];
}
// 二进制优化版本
public static int multipleKnapsackOptimized(int[] weights, int[] values, int[] counts, int capacity) {
// 将多重背包转化为0-1背包
List<Integer> newWeights = new ArrayList<>();
List<Integer> newValues = new ArrayList<>();
for (int i = 0; i < weights.length; i++) {
int count = counts[i];
// 二进制拆分
for (int k = 1; k <= count; k *= 2) {
newWeights.add(k * weights[i]);
newValues.add(k * values[i]);
count -= k;
}
if (count > 0) {
newWeights.add(count * weights[i]);
newValues.add(count * values[i]);
}
}
// 转化为0-1背包
int[] dp = new int[capacity + 1];
for (int i = 0; i < newWeights.size(); i++) {
for (int w = capacity; w >= newWeights.get(i); w--) {
dp[w] = Math.max(dp[w], dp[w - newWeights.get(i)] + newValues.get(i));
}
}
return dp[capacity];
}
}
3.4 最长公共子序列(LCS)
问题描述:给定两个字符串text1和text2,返回这两个字符串的最长公共子序列的长度。
public class LongestCommonSubsequence {
// 标准LCS解法
public static int longestCommonSubsequence(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
// 空间优化版本
public static int longestCommonSubsequenceOptimized(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[] dp = new int[n + 1];
for (int i = 1; i <= m; i++) {
int prev = 0; // 保存dp[i-1][j-1]的值
for (int j = 1; j <= n; j++) {
int temp = dp[j]; // 保存当前的dp[j](即dp[i-1][j])
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[j] = prev + 1;
} else {
dp[j] = Math.max(dp[j], dp[j - 1]);
}
prev = temp; // 更新prev为dp[i-1][j]
}
}
return dp[n];
}
// 输出具体的LCS
public static String getLCS(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
// 填充dp表
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 回溯构造LCS
StringBuilder lcs = new StringBuilder();
int i = m, j = n;
while (i > 0 && j > 0) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
lcs.append(text1.charAt(i - 1));
i--;
j--;
} else if (dp[i - 1][j] > dp[i][j - 1]) {
i--;
} else {
j--;
}
}
return lcs.reverse().toString();
}
// 扩展:最长公共子串(连续)
public static int longestCommonSubstring(String text1, String text2) {
int m = text1.length(), n = text2.length();
int[][] dp = new int[m + 1][n + 1];
int maxLength = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
maxLength = Math.max(maxLength, dp[i][j]);
} else {
dp[i][j] = 0;
}
}
}
return maxLength;
}
}
3.5 最长递增子序列(LIS)
问题描述:给定一个整数数组nums,找到其中最长严格递增子序列的长度。
public class LongestIncreasingSubsequence {
// 标准DP解法 - O(n²)
public static int lengthOfLIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int maxLength = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
maxLength = Math.max(maxLength, dp[i]);
}
return maxLength;
}
// 贪心+二分查找优化 - O(n log n)
public static int lengthOfLISOptimized(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] tails = new int[n]; // tails[i]表示长度为i+1的LIS的最小结尾值
int size = 0;
for (int num : nums) {
int left = 0, right = size;
// 二分查找找到num应该插入的位置
while (left < right) {
int mid = left + (right - left) / 2;
if (tails[mid] < num) {
left = mid + 1;
} else {
right = mid;
}
}
tails[left] = num;
if (left == size) {
size++;
}
}
return size;
}
// 输出具体的LIS
public static List<Integer> getLIS(int[] nums) {
if (nums == null || nums.length == 0) return new ArrayList<>();
int n = nums.length;
int[] dp = new int[n];
int[] prev = new int[n]; // 记录前驱节点
Arrays.fill(dp, 1);
Arrays.fill(prev, -1);
int maxIndex = 0;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j] && dp[i] < dp[j] + 1) {
dp[i] = dp[j] + 1;
prev[i] = j;
}
}
if (dp[i] > dp[maxIndex]) {
maxIndex = i;
}
}
// 回溯构造LIS
List<Integer> lis = new ArrayList<>();
while (maxIndex != -1) {
lis.add(nums[maxIndex]);
maxIndex = prev[maxIndex];
}
Collections.reverse(lis);
return lis;
}
// 扩展:最长递增子序列的个数
public static int findNumberOfLIS(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] lengths = new int[n]; // 以nums[i]结尾的LIS长度
int[] counts = new int[n]; // 以nums[i]结尾的LIS数量
Arrays.fill(lengths, 1);
Arrays.fill(counts, 1);
int maxLength = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
if (lengths[j] + 1 > lengths[i]) {
lengths[i] = lengths[j] + 1;
counts[i] = counts[j];
} else if (lengths[j] + 1 == lengths[i]) {
counts[i] += counts[j];
}
}
}
maxLength = Math.max(maxLength, lengths[i]);
}
int result = 0;
for (int i = 0; i < n; i++) {
if (lengths[i] == maxLength) {
result += counts[i];
}
}
return result;
}
}
3.6 编辑距离问题
问题描述:给定两个单词word1和word2,计算将word1转换成word2所需的最小操作次数(插入、删除、替换)。
public class EditDistance {
// 标准编辑距离解法
public static int minDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
// 初始化
for (int i = 0; i <= m; i++) {
dp[i][0] = i; // 删除所有字符
}
for (int j = 0; j <= n; j++) {
dp[0][j] = j; // 插入所有字符
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(
Math.min(dp[i - 1][j] + 1, // 删除
dp[i][j - 1] + 1), // 插入
dp[i - 1][j - 1] + 1 // 替换
);
}
}
}
return dp[m][n];
}
// 空间优化版本
public static int minDistanceOptimized(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[] dp = new int[n + 1];
// 初始化第一行
for (int j = 0; j <= n; j++) {
dp[j] = j;
}
for (int i = 1; i <= m; i++) {
int prev = dp[0]; // 保存左上角的值(dp[i-1][j-1])
dp[0] = i; // 初始化第一列
for (int j = 1; j <= n; j++) {
int temp = dp[j]; // 保存当前的dp[j](即dp[i-1][j])
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[j] = prev;
} else {
dp[j] = Math.min(
Math.min(dp[j] + 1, // 删除
dp[j - 1] + 1), // 插入
prev + 1 // 替换
);
}
prev = temp; // 更新prev为dp[i-1][j]
}
}
return dp[n];
}
// 扩展:只有删除操作的编辑距离
public static int minDeleteDistance(String word1, String word2) {
int m = word1.length(), n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; i++) {
for (int j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
dp[i][j] = i + j;
} else if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
}
}
}
return dp[m][n];
}
}
3.7 股票买卖问题系列
股票买卖问题是动态规划的经典应用,有6种常见变体。
public class StockTrading {
// 1. 买卖股票的最佳时机(一次交易)
public static int maxProfit1(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int minPrice = Integer.MAX_VALUE;
int maxProfit = 0;
for (int price : prices) {
if (price < minPrice) {
minPrice = price;
} else if (price - minPrice > maxProfit) {
maxProfit = price - minPrice;
}
}
return maxProfit;
}
// 2. 买卖股票的最佳时机(无限交易)
public static int maxProfit2(int[] prices) {
int profit = 0;
for (int i = 1; i < prices.length; i++) {
if (prices[i] > prices[i - 1]) {
profit += prices[i] - prices[i - 1];
}
}
return profit;
}
// 3. 买卖股票的最佳时机(含冷冻期)
public static int maxProfit3(int[] prices) {
if (prices == null || prices.length == 0) return 0;
int n = prices.length;
int[][] dp = new int[n][3];
// dp[i][0]: 持有股票
// dp[i][1]: 不持有股票,处于冷冻期
// dp[i][2]: 不持有股票,不处于冷冻期
dp[0][0] = -prices[0];
for (int i = 1; i < n; i++) {
// 第i天持有股票:i-1天就持有,或者i天买入(i-1天不能是冷冻期)
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
// 第i天是冷冻期:只能是i-1天卖出股票
dp[i][1] = dp[i - 1][0] + prices[i];
// 第i天不是冷冻期:i-1天就不是冷冻期或者是冷冻期
dp[i][2] = Math.max(dp[i - 1][1], dp[i - 1][2]);
}
return Math.max(dp[n - 1][1], dp[n - 1][2]);
}
// 4. 买卖股票的最佳时机(含手续费)
public static int maxProfit4(int[] prices, int fee) {
int n = prices.length;
int[][] dp = new int[n][2];
// dp[i][0]: 不持有股票
// dp[i][1]: 持有股票
dp[0][1] = -prices[0];
for (int i = 1; i < n; i++) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
// 5. 买卖股票的最佳时机(最多完成k笔交易)
public static int maxProfit5(int k, int[] prices) {
if (prices == null || prices.length == 0) return 0;
int n = prices.length;
if (k >= n / 2) {
// 相当于无限交易
return maxProfit2(prices);
}
int[][][] dp = new int[n][k + 1][2];
// 初始化
for (int j = 0; j <= k; j++) {
dp[0][j][1] = -prices[0];
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= k; j++) {
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
return dp[n - 1][k][0];
}
// 通用股票买卖问题解法
public static int maxProfitGeneral(int[] prices, int fee, int cooldown, int maxTransactions) {
// 根据参数组合调用不同的方法
if (maxTransactions == 1) {
return maxProfit1(prices);
} else if (maxTransactions == Integer.MAX_VALUE) {
if (cooldown > 0) {
return maxProfit3(prices);
} else if (fee > 0) {
return maxProfit4(prices, fee);
} else {
return maxProfit2(prices);
}
} else {
return maxProfit5(maxTransactions, prices);
}
}
}
3.8 打家劫舍系列
public class HouseRobber {
// 1. 基础打家劫舍
public static int rob1(int[] nums) {
if (nums == null || nums.length == 0) return 0;
if (nums.length == 1) return nums[0];
int n = nums.length;
int[] dp = new int[n];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[n - 1];
}
// 2. 打家劫舍II(环形数组)
public static int rob2(int[] nums) {
if (nums == null || nums.length == 0) return 0;
if (nums.length == 1) return nums[0];
// 分两种情况:抢第一家不抢最后一家,或者不抢第一家抢最后一家
return Math.max(robHelper(nums, 0, nums.length - 2),
robHelper(nums, 1, nums.length - 1));
}
private static int robHelper(int[] nums, int start, int end) {
if (start > end) return 0;
int prev2 = 0, prev1 = 0;
for (int i = start; i <= end; i++) {
int current = Math.max(prev1, prev2 + nums[i]);
prev2 = prev1;
prev1 = current;
}
return prev1;
}
// 3. 打家劫舍III(二叉树)
public static class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public static int rob3(TreeNode root) {
int[] result = robTree(root);
return Math.max(result[0], result[1]);
}
private static int[] robTree(TreeNode node) {
if (node == null) return new int[2];
int[] left = robTree(node.left);
int[] right = robTree(node.right);
// result[0]: 不抢当前节点的最大金额
// result[1]: 抢当前节点的最大金额
int[] result = new int[2];
result[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
result[1] = node.val + left[0] + right[0];
return result;
}
}
3.9 求方案数
问题描述:有一个长度为 n的数组 arr,其中元素只有 0和 1,且 arr[0] = 1和 arr[n-1] = 1。从下标 0开始,每次可以走 k步或更多步(即步长 step >= k),且每一次必须落在 1上。求走到最后一个元素(即 arr[n-1])有多少种不同的方案。
示例:
假设 arr = [1, 0, 1, 0, 1],k = 2:
-
从
0出发,可以走2步到2(因为arr[2] = 1),然后从2走2步到4(arr[4] = 1)。这是一种方案:0 -> 2 -> 4。 -
也可以从
0直接走4步到4(因为arr[4] = 1)。这是第二种方案:0 -> 4。所以总共有
2种方案。
解题思路:
这是一个典型的 动态规划(DP) 问题。我们可以用 dp[i]表示从位置 i走到终点 n-1的方案数。目标是求 dp[0]。
状态转移方程:
对于位置 i,我们可以尝试所有可能的步长 step >= k,并检查 i + step是否落在 1上:
-
如果
i + step < n且arr[i + step] == 1,则dp[i] += dp[i + step]。 -
如果
i + step == n - 1(即直接跳到终点),则dp[i] += 1。
初始化:
-
dp[n-1] = 1(已经在终点,方案数为1)。 -
其他位置的
dp[i]初始化为0。
计算顺序:
由于 dp[i]依赖于 dp[i + step](即更大的下标),我们需要 从后往前 计算 dp数组。
Java 实现:
public class Solution {
public static int countWays(int[] arr, int k) {
int n = arr.length;
if (n == 0 || arr[0] != 1 || arr[n - 1] != 1) {
return 0; // 无效输入
}
int[] dp = new int[n];
dp[n - 1] = 1; // 终点方案数为1
for (int i = n - 2; i >= 0; i--) {
if (arr[i] == 0) {
dp[i] = 0; // 不能落在0上
continue;
}
// 尝试所有可能的步长 step >= k
for (int step = k; i + step < n; step++) {
if (arr[i + step] == 1) {
dp[i] += dp[i + step];
}
}
// 检查是否可以一步跳到终点
if (i + k <= n - 1) {
dp[i] += 1;
}
}
return dp[0];
}
public static void main(String[] args) {
int[] arr = {1, 0, 1, 0, 1};
int k = 2;
System.out.println(countWays(arr, k)); // 输出 2
}
}
复杂度分析:
-
时间复杂度:
O(n^2),因为对于每个i,最坏情况下需要遍历O(n)个可能的step。 -
空间复杂度:
O(n),用于存储dp数组。
优化思路:
如果 k很大(比如接近 n),可以优化内层循环:
- •
直接检查
i + step是否能到达终点或有效的1,减少不必要的遍历。
边界情况
- •
如果
arr[0] == 0或arr[n-1] == 0,直接返回0(无法到达)。 - •
如果
k >= n,则只有1种方案(直接从0跳到n-1,前提是arr[n-1] = 1)。
示例验证:
输入 arr = [1, 0, 1, 0, 1],k = 2:
-
dp[4] = 1(终点)。 -
dp[2]:-
step = 2:2 + 2 = 4(终点),dp[2] += 1。 -
总
dp[2] = 1。
-
-
dp[0]:-
step = 2:0 + 2 = 2(arr[2] = 1),dp[0] += dp[2] = 1。 -
step = 3:0 + 3 = 3(arr[3] = 0,跳过)。 -
step = 4:0 + 4 = 4(终点),dp[0] += 1。 -
总
dp[0] = 2。
-
输出 2,与手动计算一致。
第四章:动态规划优化技巧
4.1 空间优化技巧
4.1.1 滚动数组
对于只依赖前几个状态的DP,可以使用固定大小的数组来节省空间。
// 斐波那契数列的空间优化
public int fib(int n) {
if (n <= 1) return n;
int a = 0, b = 1;
for (int i = 2; i <= n; i++) {
int c = a + b;
a = b;
b = c;
}
return b;
}
4.1.2 状态压缩
对于状态数量有限的问题,可以使用位运算来压缩状态。
// 旅行商问题的状态压缩
public int tsp(int[][] graph) {
int n = graph.length;
int[][] dp = new int[1 << n][n];
for (int[] row : dp) Arrays.fill(row, Integer.MAX_VALUE);
for (int i = 0; i < n; i++) {
dp[1 << i][i] = 0;
}
for (int mask = 0; mask < (1 << n); mask++) {
for (int i = 0; i < n; i++) {
if ((mask & (1 << i)) == 0) continue;
for (int j = 0; j < n; j++) {
if ((mask & (1 << j)) != 0) continue;
int newMask = mask | (1 << j);
dp[newMask][j] = Math.min(dp[newMask][j],
dp[mask][i] + graph[i][j]);
}
}
}
int result = Integer.MAX_VALUE;
for (int i = 0; i < n; i++) {
result = Math.min(result, dp[(1 << n) - 1][i]);
}
return result;
}
4.2 时间优化技巧
4.2.1 斜率优化
对于特定形式的状态转移方程,可以通过数学方法优化。
// 单调队列优化
public int maxSlidingWindow(int[] nums, int k) {
if (nums == null || nums.length == 0) return 0;
int n = nums.length;
int[] result = new int[n - k + 1];
Deque<Integer> deque = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
// 移除超出窗口的元素
while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
deque.pollFirst();
}
// 维护单调递减队列
while (!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offerLast(i);
if (i >= k - 1) {
result[i - k + 1] = nums[deque.peekFirst()];
}
}
return result.length > 0 ? Arrays.stream(result).max().getAsInt() : 0;
}
4.2.2 四边形不等式优化
对于区间DP问题,可以使用四边形不等式进行优化。
// 最优二叉搜索树问题的四边形不等式优化
public int optimalBST(int[] keys, int[] freq) {
int n = keys.length;
int[][] dp = new int[n + 1][n + 1];
int[][] sum = new int[n + 1][n + 1];
// 预处理前缀和
for (int i = 1; i <= n; i++) {
sum[i][i] = freq[i - 1];
for (int j = i + 1; j <= n; j++) {
sum[i][j] = sum[i][j - 1] + freq[j - 1];
}
}
int[][] root = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
dp[i][i] = freq[i - 1];
root[i][i] = i;
}
for (int length = 2; length <= n; length++) {
for (int i = 1; i <= n - length + 1; i++) {
int j = i + length - 1;
dp[i][j] = Integer.MAX_VALUE;
// 使用root表优化搜索范围
for (int r = root[i][j - 1]; r <= root[i + 1][j]; r++) {
int cost = dp[i][r - 1] + dp[r + 1][j] + sum[i][j];
if (cost < dp[i][j]) {
dp[i][j] = cost;
root[i][j] = r;
}
}
}
}
return dp[1][n];
}
第五章:动态规划实战技巧
5.1 如何识别动态规划问题
-
求最优解:问题要求最大值、最小值等
-
计数问题:求方案数、路径数等
-
可行性问题:判断是否存在某种方案
-
数据范围适中:通常n在100-1000之间
5.2 状态设计技巧
-
一维状态:dp[i] 表示前i个元素的最优解
-
二维状态:dp[i][j] 表示两个维度的状态
-
状态压缩:使用位运算表示状态集合
-
状态机:dp[i][state] 表示第i步处于某种状态
5.3 边界条件处理
// 常见的边界条件处理方式
public int dpSolution(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
if (n == 1) return nums[0];
int[] dp = new int[n + 1];
// 初始化基础情况
dp[0] = 0;
dp[1] = nums[0];
for (int i = 2; i <= n; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i - 1]);
}
return dp[n];
}
5.4 调试技巧
-
打印DP表:可视化状态转移过程
-
使用小样例:先用简单例子验证
-
边界测试:测试空数组、单元素等边界情况
-
对比暴力解法:确保DP解法的正确性
// DP表打印工具方法
public static void printDPTable(int[][] dp) {
for (int[] row : dp) {
for (int val : row) {
System.out.printf("%4d", val);
}
System.out.println();
}
System.out.println();
}
第六章:常见面试题目分类
6.1 线性DP问题
-
最大子数组和
-
最长递增子序列
-
编辑距离
-
买卖股票系列
6.2 区间DP问题
-
矩阵连乘问题
-
石子合并问题
-
最长回文子序列
-
布尔括号问题
6.3 树形DP问题
-
二叉树中的最大路径和
-
打家劫舍III
-
树上的最长路径
-
树上的最大独立集
6.4 状态压缩DP
-
旅行商问题
-
铺砖问题
-
周游问题
-
子集和问题
6.5 数位DP问题
-
数字1的个数
-
不含某些数字的数字个数
-
数字范围统计
第七章:学习资源与练习建议
7.1 推荐学习资源
-
书籍:
-
《算法导论》 - 动态规划理论基础
-
《算法竞赛入门经典》 - 实战技巧
-
《挑战程序设计竞赛》 - 高级技巧
-
-
在线平台:
-
LeetCode - 面试真题
-
Codeforces - 竞赛题目
-
AtCoder - 日本竞赛平台
-
-
视频教程:
-
MIT算法公开课
-
背包九讲视频
-
各大算法博主的动态规划专题
-
7.2 练习建议
-
由易到难:从斐波那契开始,逐步挑战更复杂的问题
-
分类练习:按问题类型集中练习
-
总结模式:归纳常见的问题模式和解题模板
-
反复练习:对于经典题目要多次练习达到熟练
7.3 常见陷阱与注意事项
-
数组越界:注意DP数组的索引范围
-
初始化错误:确保基础情况正确初始化
-
状态转移错误:仔细验证状态转移方程
-
空间复杂度:注意内存限制,必要时进行优化
-
整数溢出:使用long类型处理大数
结语
动态规划是算法领域中最美丽且实用的技术之一。掌握动态规划不仅可以帮助你在技术面试中脱颖而出,更能培养你系统化分析问题和优化解决方案的能力。
学习动态规划是一个循序渐进的过程,需要大量的练习和总结。建议从最基础的斐波那契数列开始,逐步挑战更复杂的问题,同时注意总结各种问题模式的共性。
记住,动态规划的核心在于"状态定义"和"状态转移"。只要能够正确定义状态并找出状态之间的关系,大多数动态规划问题都能迎刃而解。
希望本文能够帮助你在动态规划的学习道路上走得更远、更稳。祝你学习愉快,面试顺利!























 470
470

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










