原题的价值 出题人：VFleaking hnoi2015 集训

题目大意：

解题思路：

算法一(10分)：

暴力枚举每条边是否选取，然后统计答案就行了，再次不赘述，可以通过测试点1。

算法二(40分)：

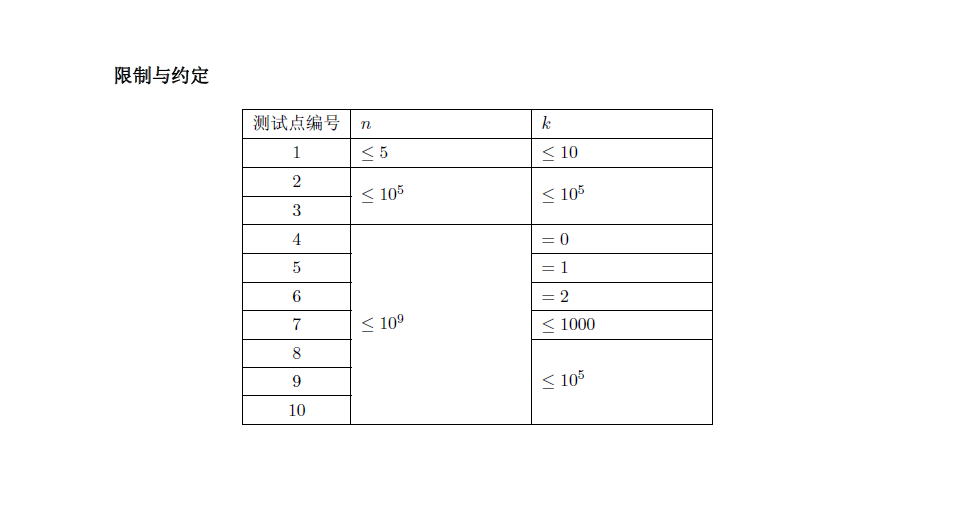
观察$4，5，6$测试点，$k=0，1，2$，打表找规律或者各种乱七八糟的方法都可以找到公式，因为本人过于懒惰(愚蠢)，所以不列出式子，让读者自己感受。

算法三(60分)：

对于$2，3$测试点，这时候就只能推导公式了QAQ，首先对于无向图，我们考虑单独的一个节点$u$,$u$的度数$d$有$d\in[0,n-1]$，我们考虑$d=i$时的情况，首先点$u$只能连出去$n-1$条边，所以如果$d=i$，那么$n-1$条边中有$i$条边是存在的，另外的是不存在的，那么贡献为${n-1\choose i} * i^k$，然后再考虑剩下的与$u$不相关的$(n-1)*(n-2)\over2$边，那么它们是可以任意选择的，所以此时对答案的贡献为$2^{(n-1)*(n-2)\over2}$，然后有$n$个点，所以$ans=(\sum_{i=0}^{n-1}{n-1\choose i}*i^k)*n*2^{(n-1)*(n-2)\over2}$，结合前面的找规律，可以得到$60$分，时间复杂度$n\log _2k$。

算法四(70分)：

对于算法三，瓶颈在于计算$\sum_{i=0}^{n-1}{n-1\choose i}*i^k$，那么我们有什么办法可以把这个东西优化一下呢？有的，就是神奇的下降阶乘幂！！！！！！！！！首先显然有${n-1\choose i}*i^\underline k (i^\underline k表示i的k次下阶幂,且i^\underline 0=0)={n-k-1\choose i-k}*(n-1)^\underline k$，所以我们如果有办法$i^k$将表示成多个i的下阶幂形式就好了，我们令$i^k=\sum_{j=0}^k(a_j*i^\underline j)$，然后我们发现$a_j$和第二类斯特林数很像(T^T，其实就是一毛一样啊)。然后我们翻看组合数学或者具体数学应该都可以找到这个式子$i^k=\sum_{j=0}^k(\begin{Bmatrix}k\\j\end{Bmatrix}*i^\underline j)$，然后就有$ans=(\sum_{i=0}^{n-1}(\sum_{j=0}^k{n-1\choose i}*\begin{Bmatrix}k\\j\end{Bmatrix}*i^\underline j))*n*2^{(n-1)*(n-2)\over2}$
$=(\sum_{i=0}^{n-1}(\sum_{j=0}^k{n-j-1\choose i-j}*\begin{Bmatrix}k\\j\end{Bmatrix}*(n-1)^\underline j))*n*2^{(n-1)*(n-2)\over2}$
$=(\sum_{j=0}^k(\sum_{i=0}^{n-1}{n-j-1\choose i-j}*\begin{Bmatrix}k\\j\end{Bmatrix}*(n-1)^\underline j))*n*2^{(n-1)*(n-2)\over2}$
$=(\sum_{j=0}^k(2^{n-j-1}*\begin{Bmatrix}k\\j\end{Bmatrix}*(n-1)^\underline j))*n*2^{(n-1)*(n-2)\over2}$
这样就可以在$k^2$时间内算出$ans$了。然后再结合算法三，就可以得到$70$分了。

算法五(100分):

观察算法四中的瓶颈，发现在求斯特林数$\begin{Bmatrix}k\\j\end{Bmatrix}$这里，那么我们有没有什么办法优化呢？答案是有的！！！！！！！！！！！！
根据第二类斯特林数的模型意义（不知道的请上网查吧），根据容斥原理，我们有$\begin{Bmatrix}k\\j\end{Bmatrix}={1\over j!}*\sum_{t=0}^k((-1)^t*\begin{pmatrix}j\\t\end{pmatrix}*(j-t)^k)$
=$\sum_{t=0}^k{(-1)^t\over t!} *{(j-t)^k\over (j-t)!}$如果我们令多项式$A(x)=\sum_{t=0}^k{(-1)^t\over t!}*x^t$
$B(x)=\sum_{t=0}^k{t^k\over t!}*x^t$，我们不难发现$\begin{Bmatrix}k\\j\end{Bmatrix}$的各项就是$A(x)$与$B(x)$的卷积，并且998244353是可以模意义下FFT的指数，果断上FFT，然后就用$k\log_2k$的时间算出了所有的$\begin{Bmatrix}k\\j\end{Bmatrix}$，然后就高高兴兴的AC了。

ps:不要问我怎么写FFT，我也不会T^T………

AC代码：

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>

using namespace std;

const long long Mod=998244353;
long long n,K;
long long S[100010]={0};
long long N=1;
long long a[300000]={0};
long long b[300000]={0};
long long c[300000]={0};

long long ksm(long long a,long long k,long long MM)
{
    long long o=1;
    for(;k;)
    {
        if(k&1)
            o=(long long)o*a%MM;
        a=(long long)a*a%MM;
        k>>=1;
    }
    return o;
}

void FFT(long long *A,int num,int flag)
{
    for(int i=0;i<num;i++)
    {
        int p=0,s=i;
        for(int j=(num>>1);j>=1;j>>=1)
        {
            p|=(s&1)*j;
            s>>=1;
        }
        if(p>i) swap(A[i],A[p]);
    }
    for(int l=2;l<=num;l<<=1)
    {
        long long w;
        if(flag==1)
            w=ksm(3,(Mod-1)/l,Mod);
        else
        {
            long long help=ksm(3,Mod-2,Mod);
            w=ksm(help,(Mod-1)/l,Mod);
        }
        for(int i=0;i<num;i+=l)
        {
            long long wk=1;
            for(int j=0;j<(l>>1);j++)
            {
                long long u=A[i+j],t=wk*A[i+j+(l>>1)]%Mod;
                A[i+j]=(u+t)%Mod;
                A[i+j+(l>>1)]=(u-t+Mod)%Mod;
                wk=wk*w%Mod;
            }
        }
    }
    if(flag==-1)
        for(int i=0;i<num;i++)
            A[i]=A[i]*ksm(num,Mod-2,Mod)%Mod;
    return;
}

int main()
{
    long long ans=0;
    freopen("value.in","r",stdin);
    freopen("value.out","w",stdout);
    cin>>n>>K;
    long long NI=1;

    long long jiecheng=1;
    int fh=1;
    for(int i=0;i<=K;i++)
    {
        if(i==0)
        {
            a[i]=1;
            b[i]=0;
        }
        else
        {
            jiecheng=jiecheng*ksm(i,Mod-2,Mod)%Mod;
            a[i]=(fh*jiecheng+Mod)%Mod;
            b[i]=ksm(i,K,Mod)*jiecheng%Mod;
        }
        fh*=-1;
    }
    N=1;
    for(;N<K+K+1;N<<=1);

    FFT(a,N,1);
    FFT(b,N,1);
    for(int i=0;i<N;i++)
        c[i]=a[i]*b[i]%Mod;
    FFT(c,N,-1);

    for(long long i=0;i<=K;i++)
    {
        if(NI==0) break;
        if(K==0)
            c[0]=1;
        ans+=c[i]*ksm(2,n-1-i,Mod)%Mod*NI%Mod;
        NI=NI*(n-i-1)%Mod;
        ans%=Mod;
    }
    ans=ans*n%Mod;
    ans=ans*ksm(2,(n-1)*(n-2)/2,Mod)%Mod;
    cout<<ans<<endl;
    fclose(stdin);
    fclose(stdout);
    return 0;
}