eclipse中,有几个项目互相引用后出现了红色感叹号,但是怎么找也找不出报错,也没缺包。这种情况下是编译错误,会影响导出jar包。

后面经过搜索发现,eclipse认为这种互相引用有问题,默认会出现编译错误error,可以改成低一点的警告方式就能通过编译。
更改地方:preferences-java-compiler-building,把circular dependencies的error级别改成warning就可以了
如下图:

修改后重新build就可以了,红色感叹号已经被干掉
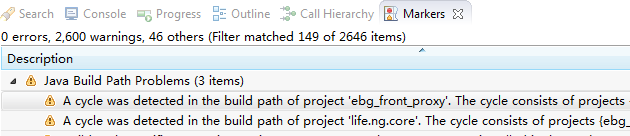
eclipse中,有几个项目互相引用后出现了红色感叹号,但是怎么找也找不出报错,也没缺包。这种情况下是编译错误,会影响导出jar包。

后面经过搜索发现,eclipse认为这种互相引用有问题,默认会出现编译错误error,可以改成低一点的警告方式就能通过编译。
更改地方:preferences-java-compiler-building,把circular dependencies的error级别改成warning就可以了
如下图:

修改后重新build就可以了,红色感叹号已经被干掉

 1243
1243
 6439
6439

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


