快速排序

       快速排序的基础是划分：划分就是在一组数据中，选择一个数作为枢轴，利用枢轴把小于枢轴的数排在枢轴的左边，大于枢轴的数排在枢轴右边。
       
       如上图所示，枢轴将数据划分为小于枢轴的部分和大于枢轴的部分，这就是划分。

talk is cheap，show me the code:

public class Partition {
    private int[] array;
    private int n;
    public Partition(int size){
        array = new int[size];
        n = 0;
    }
    public void insert(int value){
        array[n++] = value;
    }
    public void display(){
        for(int i=0;i<n;i++){
            System.out.println(array[i]);
        }
    }
    public int size(){
        return n;
    }
    public int partitionIt(int left,int right,int pivot){
        int leftPtr = left - 1;
        int rightPtr = right + 1;
        while(true){
            while(leftPtr<right && array[++leftPtr]<pivot)
                ;
            while(rightPtr>left && array[--rightPtr]>pivot)
                ;
            if(leftPtr>=rightPtr){
                break;
            }else{
                swap(leftPtr,rightPtr);
            }
        }
        return leftPtr;
    }
    public void swap(int left,int right){
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;
    }
}

public class PartitonDemo {
    public static void main(String[] args) {
        int size = 10;
        Partition partition = new Partition(size);
        partition.insert(7);
        partition.insert(1);
        partition.insert(4);
        partition.insert(2);
        partition.insert(10);
        partition.insert(3);
        partition.insert(6);
        partition.insert(9);
        partition.insert(8);
        partition.insert(5);
        System.out.println("展示数据：");
        partition.display();
        int pivot = 6;//枢轴
        System.out.println("枢轴所在位置为："+partition.partitionIt(0, size-1, pivot));
        System.out.println("展示数据：");
        partition.display();
    }
}

运行结果为：

展示数据：
7
1
4
2
10
3
6
9
8
5
枢轴所在位置为：6
展示数据：
5
1
4
2
6
3
10
9
8
7

       上面划分的栗子运用枢轴将数据划分为两个部分（小于枢轴的和大于枢轴的），但是在每一部分的内部，数据并不是有序的（尽管总体是比枢轴大或者小），但我们可以再对每一部分进行同样的划分，直到划分的粒度足够小（例如到1），那么此时所有的数据都是按照书序排列的啦。注意，每一次划分，其实最终枢轴的位置已经排列到正确的位置了，因为左边的都比它小，右边的都比它大，这样我们在每次划分时，就可以不考虑枢轴元素了，这样程序可以节省资源。

       基本的递归的快速排序的算法很简单，总结如下：

• 利用枢轴将数组划分为两部分：左边部分小于枢轴，右边部分大于枢轴
• 调用自身对左边的数据进行排序
• 调用自身对右边的数据进行排序

       下面我们取数组的最右边的数据作为枢轴，代码如下：

public class QuickSort {
    private int[] array;
    private int n;
    public QuickSort(int size){
        array = new int[size];
        n = 0;
    }
    public void display(){
        for(int i=0;i<n;i++){
            System.out.println(array[i]);
        }
    }
    public void insert(int value){
        array[n++] = value;
    }
    public void quickSortIt(){
        recQuickSort(0,n-1);
    }
    public void recQuickSort(int left,int right){
        if(left>=right){
            return;
        }else{
            int pivot = array[right];
            int partition = partitionIt(left,right,pivot);
            recQuickSort(left,partition-1);
            recQuickSort(partition+1,right);
        }
    }
    public int partitionIt(int left,int right,int pivot){
        int leftPtr = left - 1;//从左边-1出开始，先加1
        int rightPtr = right;//取到右边界，因为枢轴取得是最有边的值，此时array[++leftPtr]<pivot不满足，所以不会越界
        while(true){
            while(array[++leftPtr]<pivot)
                ;
            while(rightPtr>0 && array[--rightPtr]>pivot)
                ;
            if(leftPtr>=rightPtr){
                break;
            }else{
                swap(leftPtr,rightPtr);
            }
        }
        swap(leftPtr,right);
        return leftPtr;
    }
    public void swap(int left,int right){
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;
    }
}

public class QuickSortDemo {
    public static void main(String[] args) {
        int size = 10;
        QuickSort qs = new QuickSort(size);
        qs.insert(7);
        qs.insert(1);
        qs.insert(4);
        qs.insert(2);
        qs.insert(10);
        qs.insert(3);
        qs.insert(6);
        qs.insert(9);
        qs.insert(8);
        qs.insert(5);
        System.out.println("展示数据：");
        qs.display();
        System.out.println("***进行快速排序***");
        qs.quickSortIt();
        System.out.println("展示数据：");
        qs.display();
    }
}

运行结果为：

展示数据：
7
1
4
2
10
3
6
9
8
5
***进行快速排序***
展示数据：
1
2
3
4
5
6
7
8
9
10

       但是枢轴取最右边的数，可能有的时候并不那么理想，假设右边的数是最大的，那么这样数组就会被划分为两个数据规模相差极大的部分，例如数量为n，则最大的数（即枢轴）为一组，而其他n-1个数为一组，这样规模大的数组需要划分更多次（如果数组是倒序的，那么从右到左每个元素都需划分一次），理想状态是将数组通过枢轴划分为规模大小相近的两部分，这样快速排序的效率才会高。
       解决上面的弊端的方法一般是“使用三数据取中”来确定枢轴，如果数据总体规模小于等于3个，就不必要使用快速排序算法了，可以使用一般的比较方法（杀鸡焉用牛刀？）。
       三数据项取中：分别选取数组最左边、数组中间、数组最右边的数作为基础，然后排序这三个数，取中间的为枢轴，这时不仅有枢轴最终位置有序确定的好处，而且最左边的数一定比枢轴小，最右边的数一定比枢轴大，这样就不必担心跃出边界。

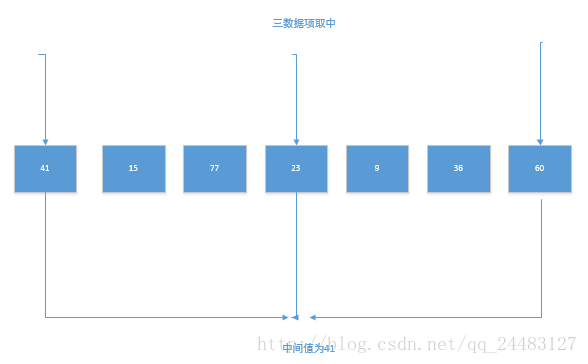
talk is cheap,show me the code:

public class QuickSort2 {
    private int[] array;
    private int n;
    public QuickSort2(int size){
        array = new int[size];
        n = 0;
    }
    public void display(){
        for(int i=0;i<n;i++){
            System.out.println(array[i]);
        }
    }
    public void insert(int value){
        array[n++] = value;
    }
    public void quickSortIt(){
        recQuickSort(0,n-1);
    }
    public void recQuickSort(int left,int right){
        int size = right-left+1;
        if(size<=3){
            manualSort(left,right);//只有三个元素，手动排序
        }else{
            int pivot = median(left,right);
            int partition = partitionIt(left,right,pivot);
            recQuickSort(left,partition-1);
            recQuickSort(partition+1,right);
        }
    }
    public int median(int left,int right){
        int mid = (left+right)/2;//取中间值
        if(array[left]>array[mid]){
            swap(left,mid);
        }
        if(array[mid]>array[right]){
            swap(mid,right);
        }
        if(array[left]>array[right]){
            swap(left,right);
        }
        swap(mid,right-1);//把枢轴放到右边倒数第二个，因为最右边的肯定比枢轴大
        return array[right-1];
    }
    public void manualSort(int left,int right){
        int size = right-left+1;
        if(size<=1){
            return;
        }else if(size==2){
            if(array[left]>array[right]){
                swap(left,right);
            }
            return;
        }else{
            if(array[left]>array[right-1]){
                swap(left,right-1);
            }
            if(array[left]>array[right]){
                swap(left,right);
            }
            if(array[left+1]>array[right]){
                swap(left+1,right);
            }
            return;
        }
    }
    public int partitionIt(int left,int right,int pivot){
        int leftPtr = left;//最右边的位置确定了（因为肯定比枢轴小）
        int rightPtr = right-1;//最右边的位置确定了（因为肯定比枢轴大），从枢轴开始
        while(true){
            while(array[++leftPtr]<pivot)
                ;
            while(array[--rightPtr]>pivot)
                ;
            if(leftPtr>=rightPtr){
                break;
            }else{
                swap(leftPtr,rightPtr);
            }
        }
        swap(leftPtr,right-1);
        return leftPtr;
    }
    public void swap(int left,int right){
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;
    }
}

public class QuickSortDemo2 {
    public static void main(String[] args) {
        int size = 10;
        QuickSort2 qs = new QuickSort2(size);
        qs.insert(7);
        qs.insert(1);
        qs.insert(4);
        qs.insert(2);
        qs.insert(10);
        qs.insert(3);
        qs.insert(6);
        qs.insert(9);
        qs.insert(8);
        qs.insert(5);
        System.out.println("展示数据：");
        qs.display();
        System.out.println("***进行快速排序***");
        qs.quickSortIt();
        System.out.println("展示数据：");
        qs.display();
    }
}

运行结果为：

展示数据：
7
1
4
2
10
3
6
9
8
5
***进行快速排序***
展示数据：
1
2
4
3
7
5
6
8
9
10

       快速排序的时间复杂度为O(N*logN),一般情况下，快速排序都是最快的。