功率谱估计

    什么是功率谱，什么是能量谱，求功率谱的过程为什么要叫做功率谱估计，为什么通常不使用传统的周期图法进行功率谱估计，这些问题再最开始进行信号处理分析的时候困扰了我很长一段时间，在网上找了很长一段时间找到了一篇比较好的英文说明文章，在此整理翻译给大家（对原文进行了适量删改，保证合理篇幅），原文可以自行Google搜索《Power Spectra  Estimation》，文章来源是National Semiconductor的Application Note 255

  

    1.介绍

    DSP 的很重要的一方面应用就是对周期信号和随机信号的功率谱估计。本文将对功率谱估计的基本概念做一个简单的介绍。

    2.什么是谱？

    谱一般是表示某周物理量数值与频率关系的一张图。常见的信号被表述成为一个随时间变化的物理量f（t），其等价的频域上的方程F（w）表示了该物理量在频域上的特征。时域和频域上的关系可以通过傅里叶分析和傅里叶变换来研究。

    傅里叶变换，时域到频域，其变换方程可以定义为：

    同时反傅里叶变化，频域到时域上的变化可以表示为：

    如果任意一个如Figure1 所示的周期信号f（t），其傅里叶变换得到的频谱中将会包含一个直流分量，一个基频成分w0，以及相应的谐波成分。（见Figure2）从Figure3中可以看出，将这些信号分量相加就可以得到原始的时间信号f（t）。

    3.能量和功率

    帕萨瓦尔定理揭示了时域和频域上的能量关系，其公式如下：

    该定理说明了信号f(t)的总能量等于其傅里叶变换后频域上的面积积分。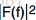一般被称作能量密度，谱密度，或者功率谱密度函数并且描述了在微分频带f到f+dF上所包含的信号能量。（译者注：此形式应该只用于能量有限信号？？？）

    为了方便起见，如果假定信号的大小为通过1欧姆的电阻的电压信号，那么信号的实时功率可以表示为信号幅度值的平方，其单位为V2·s即W。（译者注：其实从定义中可以看出来，理论上只有功率谱这个概念，而能量谱可以看做是功率谱的另外一种说法）。

    对于周期信号来说，等式（5）可以用来定义平均功率Pavg，其中T是信号的周期：

    同时，信号也能有以信号功率的方式进行表示，P（t），其中功率是能量的变化率。

    在本节的最后再做一下简单的强调，在（7b）和（8）中使用的P（t）还有，一般被称作能量密度，谱密度，或者功率谱密度函数，PSD。（译者注：此处推导建立在周期信号的基础上）PSD也可以被解释为在以频率fHz为中心的带宽为1Hz的频率带上锁信号的平均功率。

    4.随机信号

    从上面的分析中可以看到，傅里叶变换能够非常方便的处理周期信号。但是对于随机信号来说，能否也直接像周期信号一样直接进行傅里叶变换呢？答案是否定的，处理手段需要做一些简单的变换。

    首先，不加证明的陈述一个基本概念：傅里叶变换并不适用于所有的信号，主要有两点原因：

    第一点，是一个随机变量，对于任意给定的w，每个样本都有可能的样本函数集合的不同值表示。因此，x（w）不是一个过程频率表示，而只是过程的一个实现。尽管也可以通过找到这个函数的总体期望来使用x（w）在频域上表示该过程。对于平稳过程来说，还有第二个不使用有等式（1）（2）得到的x（w）的原因：就是x（w）基本上不存在。事实上，一个时域上的信号如果需要进行傅里叶变换，那么他需要满足在时域上可积的条件：

    一个功率不为零的平稳随机过程的样本永远也无法满足这个条件（除了脉冲信号等广义函数）。如果该信号为能量有限信号，哪么按照定义它的平均功率将为0。（与已知条件矛盾），在后面的章节中，我们将会看到由于条件（9）限制无法进行傅里叶变换的功率信号将可以通过统计手段来进行描述。

    假设x（t）是随机过程的一个样本函数，从中x（t）中截取一段信号定义为：

    通过定义这个截取的信号之后，就可以对XT（t）信号进行傅里叶变换（译者注：因为能量有限了）。

    截取后的信号XT（t）可以使用等式（1）和（2）进行傅里叶变换。尽管X（t）无法进行傅里叶变换，但是因为x（t）是功率信号，所以其必然含有功率谱密度谱并且功率谱密度谱的总面积是信号的平均功率。

    由帕萨瓦尔定理我们可以知道：

    同时两边同除以2T

    等式（15）左边正比于样本在-T到T上的平均功率。对于各态历经过程来说，当T趋近于无限大时，该值也逐渐接近信号的均方值。

     从这个角度上来说，T趋近于无穷大这个值并不能被取到，这是因为当T取无穷大时，XT（f）将会不存在。回忆一下，XT（f）是一个关于包含x（t）的总体样本函数的一个随机变量。因为等式（15）总是正值并且肯定存在，因此期望的极限也肯定存在。

    如果对等式（15）两边同时取期望E{}

    然后交换期望和积分顺序，同时令T趋向于无穷：

    随后可以推导得到

    其中被定义为均方值（- 表示集总平均，而<>表示为时间平均）

    对于平稳随机过程来说，均方值的时间平均值等于均方值，所以（18）可以写作：

    等式（19）的积分项，同（5b）一样，被叫做随机过程的能量密度谱或者功率谱密度函数，并且用S（f）来表示：

    回忆一下，当T趋近于无穷时，是无法进行求解期望的。功率谱密度的物理解释可以看做是平均功率，S（f）可以看成是以fHz为中心的带宽1Hz上的平均功率。S（f）的单位为V2·s并且它的积分（19）可以得到信号的均方值：

    利用等式（20）以及XT（f）是XT(t）的傅里叶变换这个事实，对于一个非稳态随机过程来说：

    注意，并且为了方便区分积分变量，（23）中对时间变量添加了下标t1及t2。（译者注：感觉上面的式子感觉指数项的符号有问题？？？，t2的指数应该为负号）

    最后，期望可以被看做是截取片段的自相关函数,Rxx(t1,t2)

    等式（25）变成了

    

    我们可以到功率谱密度是自相关函数时间平均的傅里叶变换。等式（29）适用于非平稳随机过程，而对于平稳随机过程，自相关函数和之间无关，因此

    从这里可以看出来，平稳随机过程的功率谱密度就只其自相关函数的傅里叶变换。

    这个关系被称为维纳辛钦定律（Wiener-Khintchine theorem）。

    维纳辛钦定律是分析信号的基础，因为它提供了信号时域【信号的自相关函数】和信号频域【功率谱密度】之间的关系。这里需要注意的是，对于平稳随机过程来说，信号的自相关函数是功率谱密度的逆傅里叶变换，然而对于非平稳随机变换来说，这个说法却并不成立。因为对于非平稳随机变换来说，功率谱密度的逆傅里叶变换的结果是自相关函数在时域上的平均。

    5.基础统计知识、

    假设一个随机序列x（n）是遍历随机过程x{n}的一个实现（遍历随机过程的集总平均E[]等于时间平均<>），对于所有n来说

    假设从x（n）的一部分信号中得到的随机变量{xn}的期望估计为

    并且对于每个样本序列

    由于等式（35）是当N趋近于无穷时均值的真实值，而均值的一个估计为

    下面简单介绍一些统计中的基本概念

    Bias

     

    Variance

    同时均方误差可以定义为

    Consistency

    如果当N趋近于无穷时，变差和方差都趋近于，那么就说是这个估计量是真实值的无偏估计。

    在得到均值估计量mx之后，对于正态分布的随机过程，其样本均值为

    均方值为：

    所以样本均值的方差可以表示为

    这说明了当N越大，样本均值估计量的方差越小，而其为均值的无偏估计，所以样本均值是一个无偏估计量。

    如果样本均值已知，那么样本方差也是一个无偏估计量。

    6.周期图法

    第一种方法描述了维纳辛可定理的定理公式（31）和（32），其中功率谱密度估计SNxx（f）是自相关函数估计RN学习（k

的离散傅里叶变换

    上式假设x（n）是一个拥有自相关函数RNxx（k）的离散时间随机过程。

    对于有限的序列数据

    叫做矩形数据窗，采样自相关函数为

    

    将其带入等式（71）就可以得到功率谱密度估计

    或则叫做周期图

、

    同时令

    

    

    到目前位置的推导仿佛当N变大时，推导出周期图法一种非常好的估计真实功率谱S（f）的方法，然而事实上周期图法对于功率谱的估计效果非常不理想。现对SNxx（f）的期望和方差进行分期，看其是否符合一直性估计的要求。这里有一点需要说明的是如果需要求信号的自相关函数，如果先用（74）求得信号的功率谱密度，对功率谱密度进行反傅里叶变换来求信号的自相关函数一般来说要比直接求信号的自相关函数要快。又因为周期图法求得的功率谱看起来是傅里叶变换得到频谱幅值的平方再除以N，信号的功率谱中已经抛弃了傅里叶变换频谱中有关相位的信息。

    在检查SNxx（f）的一致性之前，首先要证明信号的自相关函数具有一致性。（译者注：这里省略掉很多数据推导，直接给出结论）自相关函数的估计量是真实自相关函数的一致估计。

    对于功率谱密度（71）来说：

    将（82）带入到（95）中可以得到

    （96）中的该项可以被看做为a(k)，一个对原始数据截取造成的对真实自相关函数的一个三角窗加窗效应。因此

    并且周期图法的期望可以写作：

    从（98）中可以看色，周期图的均值是真实自相关函数和三角窗相乘之后的傅里叶变换。其结果可以看做是频域上的卷积。根据等式（98）可以得到

    

    其中三角窗的频域表示为

    对（96）或者（98）进行检查之后可以说等式（71）或者（74）给出了一个受到到变形系数a（k）影响的真实功率谱密度S（f）的无偏估计，当N越来越大时，变形系数的影响会越来越小。从这个角度来看（98）似乎依然是PSD的一个很好的估计量。然而对于估计量的方差来说，当N趋近于无穷大时，其并不趋近于零。因此周期图法并不是PSD的无偏一致估计量。因此也不能直接用于功率谱的分析。

    7.周期图平均法来进行功率谱估计

    上一节显示了周期图法并不是功率谱密度的一个一致估计。针对这个问题，Bartlett提出了一种使用周期图来对功率谱密度进行一致估计的方法，即对周期图进行平均，简单来说，Bartlett的方法通过对多个独立的周期图进行平均来减小估计量的方差。举例来说，X1，X2……XL是不相关的随机变量，拥有期望E[x]和方差，哪门他们的算术平均

    将会拥有期望E[x]和方差这说明了周期图法的方差被减小了L倍。这个过程要求将一个N点的观察数据分成L个不相邻的M点片段，随后对每个片段得到的周期图进行平均。

    更具体的说，将N点数据序列x（n），分成L个含M点的片段，

    其中上标l表示被观测的片段，下标M表示每个片段的数据点数目。根据限制，我们有N>=LM,对于L个周期图来说

    当m大于M，如果自相关函数RNxx（m）变得可以忽略（？？？），那么就可以说不同片段的周期图是相互独立的。其对应的平均周期图估计量为

    尽管这种方法求得功率谱的估计量的均值并没有变化

    但是方差却显著减小了

    这里有两点需要说明：首先如等式（110）所示，只有当L较大时，功率谱估计的方差才会比较小，才能算一个比较好的估计；第二点，（106）的偏差要比（105）的大，因为105功率谱窗的主瓣要比（106）的大。从这个角度来看，功率谱期望的偏差可以看做会影响功率谱的分辨率。需要注意的是对于给定的N点数据，增加功率谱图的数量L不仅会减少估计的方差，同时也会降低功率谱的分辨率。因此当我们使用Bartlett方法时，M和N的选择常常需要根据之前的经验来进行选择，需要在估计的方差和频率的分辨率之间做一个选择。

    8.窗函数

    在大多数情况下，我们倾向于压缩有限长度数据集两端数据的幅值来提高功率谱估计的某些特性。截取无线长原始信号的过程可以看做对原始信号乘以一个有限长的数据。例如给一个无线长的冲击响应信号乘以一个有限长度的窗函数。换句话说，窗函数决定了可以冲窗函数中观察到的原始脉冲序列的部分。

    

    这个加窗的过程类似于相关函数中的滞后窗（lag window）。除此以外，因为时域上的相乘等于频域上的卷积，因此加窗的过程也类似于将频域上频谱与窗函数进行卷积操作。注意矩形窗的傅里叶频率具有很强的振荡性，并且在高频中具有比较差的收敛性。因此将矩形窗的频谱与已知频谱进行卷积操作时，矩形窗高频的振荡特性会影响相关结果。这种情况要求我们使用其他窗函数来降低矩形窗的缺点。

    为了将窗函数频谱对目标函数功率谱真实幅值的影响降到最低，需要将窗函数的频谱近似成一个脉冲函数。也就是说窗函数的主要能量需要集中在频谱的中央。显然，理想频谱并不存在，因为理想的频谱要求窗函数具有无限的长度。

    一般来说，窗函数的频谱一般有一个主瓣，代表了频谱的中心，和主瓣旁边的许多旁瓣。我们希望窗函数能够满足以下两点标准：（1）主瓣应该尽量的窄（2）与主瓣相比，最大的旁瓣幅值应该尽可能的小。不幸的是，这两种情况不能同时达到，一般来说，使用的窗函数代表了对这两种标准的一个妥协。一个窗函数如果主瓣非常的窄，那么它就会有比较好的频率分辨率，但同时会存在一些振荡情况。相反的，如果一个窗函数的旁瓣很小，振荡现象会明显降低，但是频谱较为光滑，分辨率较低。

    9.通过窗函数来平滑单个周期图来进行谱估计

    从前面的章节中可以看出Barttlet法进行谱估计，虽然降低了方差，但是增加了均值的偏差，也降低了功率谱的频率分辨率。这几种我们将采用一种平滑操作来降低单个周期图的方差。事实上，周期图是通过将其与适当的窗函数频谱卷积来实现平滑目标的。因此Sxx（f）代表了平滑后的周期图，那么：

    因为周期图是自相关函数的傅里叶变换，而频域上的卷积等于时域上的成绩。所以

    （译者注：这里省略一部分证明）可以得到这种方法降低了谱估计的方差。

    平滑的过长想一个低通滤波器，因此降低了频率的分辨率，并且主瓣的宽度会影响平滑谱的带宽，

    我们可以看到，平滑谱的方法同样需要在分辨率和方差之间进行选择。

    10.加窗平均法来进行谱估计

    Welch提出了一种基于Bartlett法的有效测量功率谱密度的方法。这种方法在计算他们各自的周期图之前，直接将窗函数w（n）用于信号片段，如果信号被分成L段

    那么加窗周期图法为

    其中U，窗函数的能量为

    助力类似于之的平均功率图法，谱估计被定义为

    并且它的期望如下

    如果信号没有重叠，那么Welch指出，功率谱的方差为

    当不同片段之间的重叠量增加时，信号之间的相关性增加。然而如果选择一个合适的窗函数，只要不同片段之间的重叠量不是太大，增加片段数量对于能更好的降低功率谱的方差。Welch提出如果数据点N给定，那么50%的重叠量对于减少方差是比较合适的。

    11.进行功率谱估计的步骤

    对单个周期图进行平滑

    A.1.确定x（n）的自相关函数

        2.给自相关函数RNxx（k）乘一个合适的窗函数w（n）

        3.计算傅里叶变换

    B.1.计算数据集的傅里叶变换

        2.乘X（f）的共轭序列，来获得功率谱密度

        3.将功率谱密度与合适的窗函数做卷积

    C.1.计算数据集的傅里叶变换

        2.乘X（f）的共轭序列，来获得功率谱密度

        3.做反变换来获得自相关函数RNxx（k）

        4.自相关函数乘一个合适的窗函数w（n）

        4.计算功率谱

平均周期图法

    A.1.将数据x（n）分成份

        2.每一段乘以一个合适的窗函数

        3.每段做傅里叶变换

        4.3得到的频谱乘他地共轭序列得到每个片段的功率谱

        5.将各个片段的功率谱进行平均