8.5省选模拟总结

这次考挂了。。。
其实遇到了旧题，但由于种种原因坑在上面了，于是爆零了…
总结一句就是心态问题，早餐很重要~~~~

第一题 跳格子
题目大意
给定n+1个相邻的格子，标号为0~n，1~n的格子都有一个权值a[i]（整数，可能为负），给定一个v，表示一次最多跳到往后第v个格子里，求一个方案，满足从0到x再回到0，所站过格子权值和最大，且不能走重复点（除0点），往回走时站的格子必须是在已到过的格子前（即：当前站的为x，那么x+1必须已经走过，除0点）

这题我们可以用dp来解决，我们可以分析所有方案的共同点，然后分类讨论。
设f[i]表示在i开始回头的方案，一种情况是往回走时，直接跳回0，那么f[i]=0~i的正数权值和，另一种情况是必须经过一个落脚点，设为j-1，由于必须能从i跳回j-1，所以限制i-j＜v,这个可以用一个指针来限制，由于j是一定要走的，所以我们可以看做由方案j转移过来，而且j-1必走，所以设g[i]表示在i开始回头且j-1必走的方案，然后用单调队列，或线段树维护，这时有：
f[i]=max(g[j]+sum[i-1]-sum[j])+a[i] sum[j]表示前缀正数和（当然，你可以在线段树维护时用区间加，我用的是后者）
g[i]=f[i]+(a[i-1]<0)*a[i-1] (因为当a[i-1]＜0时，并没有加入f[i]内)
*有一种情况比较特殊，往回走到i-1里，这里我们可以看做i-1方案，j走到i-1时，先从j走到i再往回走到i-1，因为满足i-1-j＜v，所以j是可以走到i的

贴代码

#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#define N 300001
#define MINX -5000000000000000
using namespace std;
int n,v;
int a[N];
long long ans1;
long long b[N],f[N*4][2],ans[N],c[N];
void init(){
    scanf("%d %d",&n,&v);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
}
void down(int l,int r,int s){
    if (f[s][1]){
        f[s][0]+=f[s][1];
        if (l!=r)f[s+s][1]+=f[s][1],f[s+s+1][1]+=f[s][1];
        f[s][1]=0;
    }
}
void up(int l,int r,int s,int ll,int rr,int v){
    down(l,r,s);
    if (r<ll||rr<l)return;
    if (ll<=l&&r<=rr){
        f[s][1]=v;
        down(l,r,s);
        return;
    }   
    up(l,(l+r)/2,s+s,ll,rr,v),up((l+r)/2+1,r,s+s+1,ll,rr,v);
    f[s][0]=max(f[s+s][0],f[s+s+1][0]);
}
long long get(int l,int r,int s,int ll,int rr){
    down(l,r,s);
    if (r<ll||rr<l)return MINX;
    if (ll<=l&&r<=rr)return f[s][0];
    return max(get(l,(l+r)/2,s+s,ll,rr),get((l+r)/2+1,r,s+s+1,ll,rr));
}
void ins(int l,int r,int s,int ll){
    down(l,r,s);
    if (l==r){
        f[s][0]=ans[l-1];
        if (a[ll-1-1]<0)f[s][0]+=a[ll-1-1];
        return;
    }
    static int ss;
    if ((ss=(l+r)/2)>=ll)ins(l,ss,s+s,ll);
    else
        ins(ss+1,r,s+s+1,ll);
    f[s][0]=max(f[s+s][0],f[s+s+1][0]);
}
void work(){
    static int l;
    n++,l=0;
    for (int i=1;i<=v;i++)
        if (a[i]>0)ans1+=a[i];
    for (int i=1;i<n;i++){
        if (i-l==v)l++;
        ans[i]=max(get(1,n,1,l+1,i),c[i-1])+a[i];
        c[i]=ans[i];
        ans1=max(ans[i],ans1);
        ins(1,n,1,i+1);
        if (a[i]>0)up(1,n,1,l+1,i,a[i]);
    }
}
void write(){
    printf("%lld",ans1);
}
int main(){
    init();
    work();
    write();
    return 0;
}

时间复杂度 nlogn

第二题 数三角形
题目大意
给定n个点，求有多少个三角形（这n个点组成）包含原点。

cf有类似的原题

方法一：（我以前的方法，正着做）
我们可以发现，对于已知两个点，要想再有一个点使得所构成的三角形合法，则有第三个点必定在该两个点与原点连线的反向延长线内（如阴影部分）

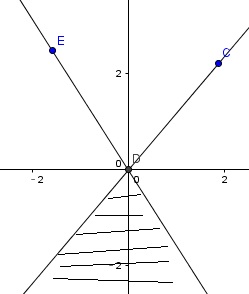
那么我们可以通过预处理，所有点对原点反向延长线的顺时针方向点数，用R-L来得到

然而要枚举两个点会超时，我们发现，对于这样的点对，若已知一个点，那么另一个点必定在其顺时针（这里我们同一一个方向才可以避免重复计算）180°的范围内，这样我们可以对之前的预处理进行前缀和和后缀和，同样用R-L解决，当然还会有多出来的部分要减去，细节要处理好。
时间复杂度nlogn
贴代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 100001
#define PI 3.1415926535898
int n,m;
long long ans;
long long f[N],up[N],down[N];
int a[N][2],b[N];
double c[N];
void init(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++)scanf("%d %d",&a[i][0],&a[i][1]),b[i]=i;
}
bool cmp(int x,int y){return c[x]<c[y];}
int er(double s){
    static int l,r,m;
    l=1;r=n;
    while (l<=r)if (c[b[m=(l+r)/2]]>s)r=m-1;else l=m+1;
    return l;
}
double did(double x){
    static double s=PI+PI;
    return x>=s?x-s:x;
}
int calc(double x1,double y1){
    static int x,y,s;
    x=er(x1),y=er(y1);
    while (c[b[x]]<x1&&x<=n)x++;
    if (y>n)y--;
    while (c[b[y]]>y1&&y)y--;
    if (x1<=y1)s=y-x+1;else{
        s=0;
        if (x<=n&&c[b[x]]>=x1)s+=n-x+1;
        if (y&&c[b[y]]<=y1)s+=y;
    }
    return s;
}
void add(int x){
    static int l,r,m;
    static double s;
    s=c[b[x]]+PI;
    l=x,r=n;
    while (l<=r)if (c[b[m=(l+r)/2]]<s)l=m+1;else r=m-1;
    if (l>n)l=n;
    while (c[b[l]]>s)l--;
    ans+=(down[l-1]-down[x-1]-(f[l-1]-f[x-1])*(n-l+1));
    if (n!=l)ans=ans+up[n]-up[l]-(f[n]-f[l])*l;
    if (x>1)ans+=f[x-1]*(n-l);
}
void work(){
    static int x,y;
    static double s;
    x=0,y=0;
    s=PI+PI;
        for (int i=1;i<=n;i++){
            c[i]=atan2(a[i][1]-=y,a[i][0]-=x);
            if (c[i]<0)c[i]+=s;
        }
        sort(b+1,b+n+1,cmp);
        ans=0;
        for (int i=1;i<n;i++)
            f[i]=f[i-1]+calc(did(c[b[i]]+PI),did(c[b[i+1]]+PI));
        f[n]=f[n-1]+calc(did(c[b[n]]+PI),did(c[b[1]]+PI));
        for (int i=1;i<=n;i++)
            up[i]=up[i-1]+(f[i]-f[i-1])*i,down[i]=down[i-1]+(f[i]-f[i-1])*(n-i+1);
        for (int i=1;i<n;i++)add(i);
        for (int i=1;i<=n;i++)a[i][1]+=y,a[i][0]+=x;
        printf("%lld\n",ans/3);
}
int main(){
    init();
    work();
    return 0;
}

方法二（正难则反）
我们可以用n*（n-1）*（n-2）/6的总方案减去不合法的方案

我们对于已知的一个点c，不合法方案一定形如：

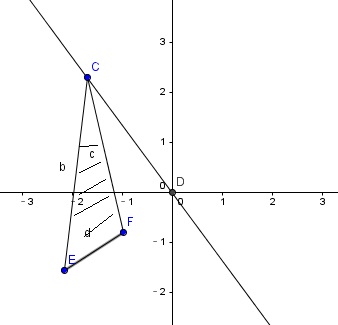
（我们假定都落在在点c与原点连线的同一侧，避免重复计算）
这样，通过枚举点c，求出点c与原点连线同侧的点数sum，用ans减去sum*（sum-1）/2
时间复杂度 nlogn

贴代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 100002
#define PI M_PI
int n,mid;
long long ans;
long double c[N+N];
long double did(long double x){
    if (x>PI+PI)x-=PI+PI;
    return x<0?x+PI+PI:x;
}
void init(){
    static int x,y;
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d %d",&x,&y),c[i]=did(atan2(y,x));
}
void pre(){
    static int x;
    sort(c+1,c+n+1);
    for (int i=1;i<=n;i++)
        c[i+n]=c[i]+PI+PI;
}
int did1(int x){
    return x<0?x+n:x;
}
void work(){
    static int l,a;
    static long double x;
    ans=(long long)n*(n-1)*(n-2)/2/3;
    for (int i=1;i<=n;i++){
        x=c[i]+PI;
        while (l<n+N&&c[l+1]<=x)l++;
        a=l-i;
        ans-=(long long)a*(a-1)/2;
    }
}
void write(){
    printf("%lld",ans);
}
int main(){
    init();
    pre();
    work();
    write();
    return 0;
}

第三题 STR（图片来源：解题报告）
题目大意
　平面上有z个点，给你p个形如 p1(x1,y1),p2(x2,y2) 的询问，要你求出z个点中离p1更近的点，离p2更近的点，与p1和p2的距离相等的点各有多少个。这里的距离指的是曼哈顿距离，即x坐标之差的绝对值加上y坐标之差的绝对值。

我们可以仔细分析得出最后的答案形如：

可以发现最终我们只要解决这几种：

第一个可以通过排序，二分查找或扫描得到

第二种可以将询问离线，沿y轴或x轴扫描线得到，也可以用主席树（空间64M还是可以接受的）

第三种就比较“无耻”的麻烦了，也是询问离线，我们可以用x+y（可以发现一定是135°）（另一种斜率自己yy吧..）表示一个点被哪条135°的斜线经过（可以看做斜线与y轴交点），排序x+y后插入时按x插入（即沿45°方向扫描）

据观察，第三种要做8次扫描线..由于编程较复杂，代码量较大，还没打出来，故不贴代码。。