8.6省选模拟总结

今天被低2届的虐暴了….
感觉最近状态有点低迷，做题速度低下..要多到网上刷题才行！

第一题 删数字

题目大意
给你一个N 个数组成的序列V，要你删除其中K 个数，M 表示剩下的数字中任意两个数的差值的最大值，m 表示最小差值，要你计算删除K 个数后，M+m
的最小值。

这题我一下在脑抽了..

排序后可以发现若维护一个长度为n-k的数列，中间的数一定不会删(这个我没想到….虽然我知道要排序，但还是认为中间有可能删…)，这样会同时放大M和m，所以答案一定是一个连续的数列，枚举右边界，然后用单调队列来维护m，当左边界移动时，消除队列中不合法的数即可。

贴代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
#define N 1000001
int n,m,l,r;
int ans;
int d[N][2],a[N];
void init(){
    scanf("%d %d",&n,&m);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
}
void did(int x,int y){
    d[x][0]=d[y][0],d[x][1]=d[y][1];
}
void work(){
    sort(a+1,a+n+1);
    m=n-m;
    l=1,r=0;
    for (int i=2;i<=m;i++){
        d[++r][0]=i-1,d[r][1]=a[i]-a[i-1];
        while (r>1&&d[r][1]<d[r-1][1])did(r-1,r),r--;
    }
    ans=d[l][1]+a[m]-a[1];
    for (int i=m+1;i<=n;i++){
        d[++r][0]=i-1,d[r][1]=a[i]-a[i-1];
        while (i-d[l][0]+1>m)++l;
        while (r>l&&d[r][1]<d[r-1][1])did(r-1,r),r--;
        ans=min(ans,d[l][1]+a[i]-a[i-m+1]);
    }
}
void write(){
    printf("%d",ans);
}
int main(){
    init();
    work();
    write();
    return 0;
}

第二题 最短路
N 个结点、M 个含K 个结点的完全子图构成一个奇怪的图，问从结点1 走
到结点N 最少需要经过多少个结点。

一开始我以为可以过的，被卡了一个点，超时…

方法一：我们可以将图改造一下，将点1、n单独出来，将完全子图看做是点，当两个完全子图含同一个数字时将两个图（点）连边，还要将1、n向包含它们的子图连边。（这部分我用m^2*k来打，超时了，也可以用位运算强行加速，速）
最后跑个bfs+1就是答案了。

方法二：连边方案和前面的有所不同，每个数字记录下它所在的完全子图，bfs时先找出点x所在的完全子图，下一步向完全子图里的其他点走。

温馨提示：记录一下完全子图是否已被到达过，到过了的不再走，不然会超时的…

贴代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 100001
#define M 1002
using namespace std;
int n,m,ans,k;
bool bz[M];
int f[N],a[M*M*2][2],g[N],b[M][M],d[N+10];
void ins(int x,int y){
    static int sum=0;
    a[++sum][0]=y,a[sum][1]=g[x],g[x]=sum;
}
void init(){
    scanf("%d %d %d",&n,&k,&m);
    for (int i=1;i<=m;i++)
        for (int j=1;j<=k;j++)
            scanf("%d",&b[i][j]),ins(b[i][j],i);
}
void spfa(){
    static int l,r,x;
    d[1]=1,f[1]=1,l=0,r=1;
    while (l<r){
        for (int i=g[d[++l]];i;i=a[i][1])
            if (!bz[x=a[i][0]]){
                bz[x]=1;
                for (int j=1;j<=k;j++)
                    if (!f[b[x][j]])
                        f[b[x][j]]=f[d[l]]+1,d[++r]=b[x][j];
            }
    }
}
void work(){
    m++;
    spfa();
    ans=f[n];
    if (!f[n])ans--;
}
void write(){
    printf("%d",ans);
}
int main(){
    init();
    work();
    write();
    return 0;
}

第三题 病毒
题目：
病毒扩散了！村庄中共有M 个人，编号为0 到M-1，病毒症状只会持续一天，每个人可能多次感染病毒。
第一天，若干个病毒携带者感染了病毒，病毒扩散就是由病毒携带者引起的，从第二天开始的每一天，编号P 的人在以下条件下就会感染病毒：(a*b)mod M=P(其中a 为前一天感染病毒的某一个人的编号，b 是其中一个病毒携带者的编号，a 和b 可能相同)
例如村庄共101 个人，病毒携带者编号为5 和50，第一天感染病毒的为5和50，第二天有25，48(250 mod 101)和76(2500 mod 101)，第三天77 会感染病毒，因为(48*50) mod 101=77
问第K 天哪些人会感染病毒。

可以发现，f[0]=1,f[i]=f[i-1]*E（乘法为两个数组内的数字两两相乘取mod，E是初始读入的数组）乘法满足结合律，快速幂就行了。。

贴代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#define N 1501
using namespace std;
int m,top;
long long k;
int b[N],c[N],a[N],bz[N];
void init(){
    scanf("%lld %d %d",&k,&m,&b[0]);
    for (int i=1;i<=b[0];i++)
        scanf("%d",&b[i]);
}
void cheng(int*a,int*b,int*c){
    static int sum=0,y;
    ++sum,c[0]=0;
    for (int i=1;i<=a[0];i++)
        for (int j=1;j<=b[0];j++)
            if (bz[y=a[i]*b[j]%m]!=sum)bz[y]=sum,c[++c[0]]=y;
}
void work(int*a,int*b,int*c){
    a[0]=a[1]=1;
    while (k){
        if (k&1)cheng(a,b,c),swap(a,c);
        cheng(b,b,c),swap(b,c);
        k/=2;
    }
    sort(a+1,a+a[0]+1);
    for (int i=1;i<=a[0];i++)
        printf("%d ",a[i]);
}
int main(){
    init();
    work(a,b,c);
    return 0;
}

第四题 屏保
题目：
你最近安装了一个新的屏幕保护程序，如果你离开键盘5 分钟，屏保将会显示一个有热带鱼的水族馆，水族馆的底端是由沙石形成的供鱼玩耍的地方，沙石的高度可以设置，水位也可以设置。
水族馆可以看做是一个二维平面，宽看作N-1 列，最左端的横坐标为0，最右端横坐标为N-1，每个整数横坐标都对应着一个沙石的高度H_i(0<=i<=N-1)，相邻横坐标i 和i+1 之间的沙石可以看做是由(i,H_i)和(i+1,H_i+1)这两个点形成的线段。
如果水位为h，水覆盖着水族馆底端到y=h 这个区域，如果有部分沙石在水面以上，这部分形成一个岛屿。对于不同的沙石情况，你想知道被水覆盖区域的面积，即水位以下总面积减去水中沙石的面积。

正如题目所说，我们可以用水位以下总面积减去水中沙石的面积得到答案，那么我们只需维护水高1~H（1000）时的砂石面积即可（线段树）。

对于砂石，我们可以维护相邻视为一种通常情况：

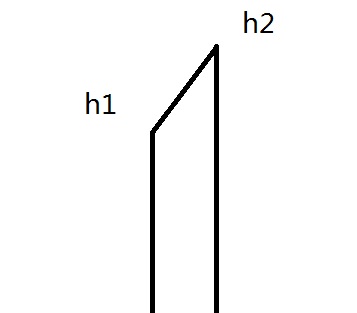
设h1为较低高度，h2为较高高度，h为水高

那么当h≤h1时，砂石面积=h

当h1＜h≤h2时，我们可以拆分成一个矩形面积（常数h1）和一个梯形面积，
对于梯形面积，我们引入h3=h2-h1，用相似三角形可得，S=h3/2-(h2-h)^2/h3/2,展开可得到关于h的常数、一次、二次项系数，分别加入线段树里

当h2＜h时，砂石面积=（h1+h2）/2

对于以上的修改，可看做对线段树里的常数、一次、二次项系数修改，查询时将标记下传到最底层后计算即可得到答案。

贴代码

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#define N 100001
#define H 1000
using namespace std;
int n,m;
int a[N];
double f[H*4+1][3];
double ans;
void init(){
    scanf("%d %d",&n,&m);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
}
void down(int l,int r,int s){
    if (l!=r){
        f[s+s][0]+=f[s][0],f[s+s+1][0]+=f[s][0];
        f[s+s][1]+=f[s][1],f[s+s+1][1]+=f[s][1];
        f[s+s][2]+=f[s][2],f[s+s+1][2]+=f[s][2];
        f[s][0]=f[s][1]=f[s][2]=0;
    }
}
void change(int l,int r,int s,int ll,int rr,double x,double y,double z){
    if (r<ll||rr<l)return;
    if (ll<=l&&r<=rr){
        f[s][0]+=x,f[s][1]+=y,f[s][2]+=z;
        return;
    }
    change(l,(l+r)/2,s+s,ll,rr,x,y,z),change((l+r)/2+1,r,s+s+1,ll,rr,x,y,z);
}
void find(int l,int r,int s,int ll){
    down(l,r,s);
    if (l==r){
        ans=f[s][0]+f[s][1]*l+f[s][2]*l*l;
        return;
    }
    static int ss;
    if ((ss=(l+r)/2)>=ll)find(l,ss,s+s,ll);
    else
        find(ss+1,r,s+s+1,ll);
}
void did(int x,int y,double z){
    static double h1,h2,h3;
    if (!x)return;
    if (y>n)return;
    h1=a[x],h2=a[y];
    if (h1>h2)swap(h1,h2);
    h3=h2-h1;
    if (h1>=1)
    change(1,H,1,1,h1,0,z,0);
    if (h1<h2)
    change(1,H,1,h1+1,h2,(h1+h3/2-h2*h2/(2*h3))*z,(h2/h3)*z,(-1/(2*h3))*z);
    change(1,H,1,h2+1,H,(h1+h2)/2*z,0,0);
}
void pre(){
    for (int i=2;i<=n;i++)
        did(i-1,i,1);
}
void work(){
    static int x,y;
    static char c;
    for (;m--;){
        scanf(" %c",&c);
        if (c=='Q'){
            scanf("%d",&x);
            if (!x)printf("0.000\n");
            else{
                find(1,H,1,min(x,H));
                ans=(n-1)*x-ans;
                printf("%.3f\n",ans);
            }
        }else{
            scanf("%d %d",&x,&y);
            x++;
            did(x-1,x,-1);
            did(x,x+1,-1);
            a[x]=y;
            did(x-1,x,1);
            did(x,x+1,1);
        }
    }
}
int main(){
    init();
    pre();
    work();
    return 0;
}