一文彻底搞懂Floyd算法（弗洛伊德算法）

Floyd 算法（弗洛伊德算法）专门用来在网（带权的图）中查找各个顶点之间的最短路径。

关于网（带权的图），如果读者不清楚是什么，可以阅读我之前写的一篇文章，专门讲解了数据结构中关于图的定义和种类：

图存储结构，数据结构中的图从本节开始，我将为大家介绍最后一种存储结构，也是数据结构中最复杂、难掌握的存储结构 图 。 图结构常用来存储逻辑关系为多对多的数据。比如说，一个学生可以同时选择多门课https://xiexuewu.github.io/view/338.html要想彻底理解 Floyd 算法，读者首先要搞清楚什么是最短路径。

最短路径是什么

对于逻辑关系为“多对多”的数据集，数据结构中推荐用图结构来存储。

在给定的一张图中，一个顶点到另一个顶点的路径可能有多条，最短路径指的就是顶点之间“最短”的路径。

举个简单的例子：

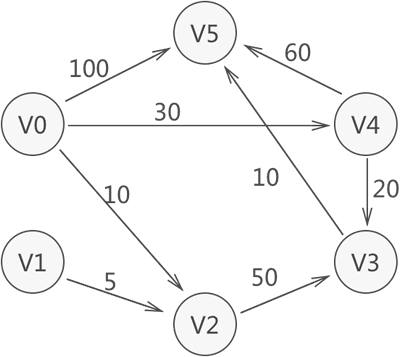
上图不仅是一张图，顶点之间的边还带有权值，比如 V1 到 V2 这条边的权值为 5，因此更确切的说，这是一张网，而且是有向网。

在不同的场景中，路径“最短”的含义也有所差异，比如途径顶点数量最少、总权值最小等。提到最短路径，往往指的是总权值最小的路径，所以常常在网结构（带权的图）中讨论最短路径问题，包括有向网和无向网。

观察上图中的这张网，从 V0 到 V5 的路径有多条，包括：

1. V0 -> V5，总权值为 100
2. V0 -> V4 -> V5，总权值为 30+60 = 90
3. V0 -> V4 -> V3 -> V5，总权值为 30+20+10 = 60
4. V0 -> V2 -> V3 -> V5，总权值为 10+50+10 = 70

通过比较这些路径的总权值，发现第 3 条路径的权值最短，因为 V0 -> V4 -> V3 -> V5 就是从 V0 到 V5 的最短路径。

现如今，大家出行再也不用担心找不到路了，车上有车载导航，手机上也可以安装各种导航 App，只要输入目的地，导航会自动帮我们规划一条距离最短的路线，这是最短路径在实际生活中的典型应用之一。

在指定的一张图或者网中查找最短路径，常用的解决方案有两个，分别是 Dijkstra 算法和 Floyd（弗洛伊德）算法。本节我重点讲解 Floyd 算法。

Floyd算法

在给定的带权图中，两个顶点之间的最短路径可能会经过多个（≥0）其它顶点。

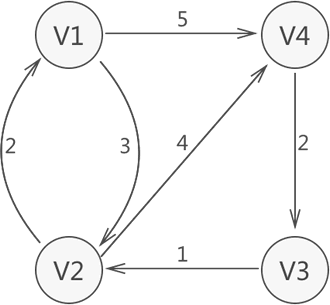
图 1 有向带权图

图 1 中，V4-V1 的最短路径是 V4->V3->V2->V1，中间就经过了 V3 和 V2 两个顶点。当然，有一些顶点之间的最短路径不经过任何顶点，比如图 1 中 V1-V2 的最短路径就是 V1->V2。

因此查找两个顶点之间的最短路径，就是找一条“中间可能经过某些顶点”且权值最小的路径。Floyd 算法的实现思路是：逐一试探图中的各个顶点，将它们作为各个顶点之间路径上的中间顶点，如果能找到一条权值更小的路径，就将此路径记录下来，反之继续试探其它的顶点。

仍以图 1 为例，Floyd 算法查找各个顶点之间最短路径的过程是：
1) 建立一张表格，记录各个顶点直达其它顶点的路径权值：

表 1 各个顶点之间直达的路径权值

		目标顶点
		V1	V2	V3	V4
起始顶点	V1	0	3	∞	5
	V2	2	0	∞	4
	V3	∞	1	0	∞
	V4	∞	∞	2	0

2) 在表 1 的基础上，将 V1 作为各个顶点之间路径上的中间顶点：

• V2->V1->V3：权值为 2 + ∞ = ∞，表 1 中记录的 V2->V3 的权值也是 ∞；
• V2->V1->V4：权值为 2 + 5 = 7，表 1 中记录的 V2->V4 的权值是 4；
• V3->V1->V2：权值为 ∞ + 3 = ∞，表 1 中记录的 V3->V2 的权值是 1；
• V3->V1->V4：权值为 ∞ + 5 = ∞，表 1 中记录的 V3->V4 的权值是 ∞；
• V4->V1->V2：权值为 ∞ + 3 = ∞，表 1 中记录的 V4->V2 的权值是 ∞；
• V4->V1->V3：权值为 ∞ + ∞ = ∞，表 1 中记录的 V4->V3 的权值是 2。 

将 V1 作为各个顶点间路径上的中间顶点，并没有找到权值更小的路径。

3) 试探完 V1 的基础上，将 V2 作为各个顶点之间路径上的中间顶点：

• V1->V2->V3：权值为 3 + ∞ = ∞，表 1 中记录的 V1->V3 的权值为 ∞；
• V1->V2->V4：权值为 3 + 4 = 7，表 1 中 V1->V4 的权值为 5；
• V3->V2->V1：权值为 1 + 2 = 3，表 1 中 V3->V1 的权值为 ∞，3 < ∞；
• V3->V2->V4：权值为 1 + 4 = 5，表 1 中 V3->V4 的权值为 ∞，5 < ∞；
• V4->V2->V1：权值为 ∞ + 2 = ∞，表 1 中 V4->V1 的权值为 ∞；
• V4->V2->V3：权值为 ∞ + ∞ = ∞，表 1 中 V4->V3 的权值为 2。

在途径 V2 顶点的这些路径中，找到了比 V3->V1 和 V3->V4 权值更小的路径，将它们记录到表格中：

表 2 各个顶点之间直达的路径权值

		目标顶点
		V1	V2	V3	V4
起始顶点	V1	0	3	∞	5
	V2	2	0	∞	4
	V3	3（V3->V2->V1）	1	0	5（V3->V2->V4）
	V4	∞	∞	2	0

4) 试探完 V1 和 V2 的基础上，将 V3 作为各个顶点之间路径上的中间顶点：

• V1->V3->V2 权值为 ∞ + 1 = ∞，表 2 中 V1->V2 的权值为 3；
• V1->V3->V4 权值为 ∞ + 5 = ∞，表 2 中 V1->V4 的权值为 5；
• V2->V3->V1 权值为 ∞ + 3 = ∞，表 2 中 V2->V1 的权值为 2；
• V2->V3->V4 权值为 ∞ + 5 = ∞，表 2 中 V2->V4 的权值为 4；
• V4->V3->V1 权值为 2 + 3 = 5，表 2 中 V4->V1 的权值为 ∞，5 < ∞；
• V4->V3->V2 权值为 2 + 1 = 3，表 2 中 V4->V2 的权值为 ∞，3 < ∞；

在途径 V3 顶点的这些路径中，找到了比 V4->V1 和 V4->V2 权值更小的路径，将它们记录到表格中：

表 3 各个顶点之间直达的路径权值

		目标顶点
		V1	V2	V3	V4
起始顶点	V1	0	3	∞	5
	V2	2	0	∞	4
	V3	3（V3->V2->V1）	1	0	5（V3->V2->V4）
	V4	5（V4->V3->V2->V1）	3（V4->V3->V2）	2	0

5) 试探完 V1、V2 和 V3 的基础上，将 V4 作为各个顶点之间路径上的中间顶点：

• V1->V4->V2 权值为 5 + 3 = 8，表 3 中 V1->V2 的权值为 3；
• V1->V4->V3 权值为 5 + 2 = 7，表 3 中 V1->V3 的权值为 ∞，7 < ∞；
• V2->V4->V1 权值为 4 + 5 = 9，表 3 中 V2->V1 的权值为 2；
• V2->V4->V3 权值为 4 + 2 = 6，表 3 中 V2->V3 的权值为 ∞，6 < ∞；
• V3->V4->V1 权值为 4 + 5 = 9，表 3 中 V3->V1 的权值为 3；
• V3->V4->V2 权值为 5 + 5 = 10 ，表 3 中 V3->V2 的权值为 1。

在途径 V4 顶点的这些路径中，找到了比 V1->V3 和 V2->V3 权值更小的路径，将它们记录到表格中：

表 4 各个顶点之间直达的路径权值

		目标顶点
		V1	V2	V3	V4
起始顶点	V1	0	3	7（V1->V4->V3）	5
	V2	2	0	6（V2->V4->V3）	4
	V3	3（V3->V2->V1）	1	0	5（V3->V2->V4）
	V4	5（V4->V3->V2->V1）	3（V4->V3->V2）	2	0

6) 图中的所有顶点都被试探了一遍，Floyd 算法执行结束，表 4 记录的就是各个顶点之间的最短路径。

深入理解Floyd算法

Floyd 算法查找最短路径的过程中，每一次试探都利用了前面推导出的结论，例如将 V3 作为中间顶点时，找到了 V4->V3->V2->V1 这条更短的路径，其中 V3->V2->V1 是在 V2 作为中间顶点时找到的。

因此分别将 V1、V2、V3 和 V4 作为中间顶点的过程，本质上是：

• 将 V1 作为各个顶点间路径上的中间顶点，查找更短的路径；
• 有了 V1 作为中间顶点的路径信息，接下来再将 V2 作为中间顶点，此时各个路径上的中间顶点可能出现 V1 和 V2，如果路径的权值更短，会记录到表格中；
• 有了 V1、V2 作为中间顶点的路径信息，接下来再将 V3 作为中间顶点，此时各个路径上的中间顶点可能出现 V1、V2 和 V3，如果路径的权值更短，会记录到表格中；
• 有了 V1、V2、V3 作为中间顶点的路径信息，接下来再将 V4 作为中间顶点，此时各个路径上的中间顶点可能出现 V1、V2、V3 和 V4，如果记录的权值更短，会记录到表格中。

最终，图中的顶点都可能作为各个路径上的中间顶点，表格中记录的都是各个顶点之间权值最小的路径，它们也一定是最短路径。

Floyd算法的具体实现

实现Floyd算法，可以参考如下 C 语言程序：

#include <stdio.h>
#define MAX_VERtEX_NUM 20                   //顶点的最大个数
#define VRType int                          //表示弧的权值的类型
#define VertexType int                      //图中顶点的数据类型
#define INFINITY 65535
typedef struct {
    VertexType vexs[MAX_VERtEX_NUM];        //存储图中顶点数据
    VRType arcs[MAX_VERtEX_NUM][MAX_VERtEX_NUM];                         //二维数组，记录顶点之间的关系
    int vexnum, arcnum;                      //记录图的顶点数和弧（边）数
}MGraph;

typedef int PathMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];     //用于存储最短路径中经过的顶点的下标
typedef int ShortPathTable[MAX_VERtEX_NUM][MAX_VERtEX_NUM]; //用于存储各个最短路径的权值和

//根据顶点本身数据，判断出顶点在二维数组中的位置
int LocateVex(MGraph* G, VertexType v) {
    int i;
    //遍历一维数组，找到变量v
    for (i = 0; i < G->vexnum; i++) {
        if (G->vexs[i] == v) {
            break;
        }
    }
    //如果找不到，输出提示语句，返回-1
    if (i > G->vexnum) {
        printf("no such vertex.\n");
        return -1;
    }
    return i;
}

//构造有向网
void CreateUDG(MGraph* G) {
    int i, j;
    int v1, v2, w;
    int n, m;
    scanf("%d,%d", &(G->vexnum), &(G->arcnum));
    for (i = 0; i < G->vexnum; i++) {
        scanf("%d", &(G->vexs[i]));
    }
    for (i = 0; i < G->vexnum; i++) {
        for (j = 0; j < G->vexnum; j++) {
            G->arcs[i][j] = INFINITY;
        }
    }
    for (i = 0; i < G->arcnum; i++) {
        scanf("%d,%d,%d", &v1, &v2, &w);
        n = LocateVex(G, v1);
        m = LocateVex(G, v2);
        if (m == -1 || n == -1) {
            printf("no this vertex\n");
            return;
        }
        G->arcs[n][m] = w;
    }
}

//弗洛伊德算法，其中P二维数组存放各对顶点的最短路径经过的顶点，D二维数组存储各个顶点之间的权值
void ShortestPath_Floyed(MGraph G, PathMatrix P, ShortPathTable D) {
    int v, w, k;
    //对P数组和D数组进行初始化
    for (v = 0; v < G.vexnum; v++) {
        for (w = 0; w < G.vexnum; w++) {
            D[v][w] = G.arcs[v][w];
            P[v][w] = -1;
        }
    }
    //拿出每个顶点作为遍历条件
    for (k = 0; k < G.vexnum; k++) {
        //对于第k个顶点来说，遍历网中任意两个顶点，判断间接的距离是否更短
        for (v = 0; v < G.vexnum; v++) {
            for (w = 0; w < G.vexnum; w++) {
                //判断经过顶点k的距离是否更短，如果判断成立，则存储距离更短的路径
                if (D[v][w] > D[v][k] + D[k][w]) {
                    D[v][w] = D[v][k] + D[k][w];
                    P[v][w] = k;
                }
            }
        }
    }
}

// 中序递归输出各个顶点之间最短路径的具体线路
void printPath(PathMatrix P, int i, int j)
{
    int k = P[i][j];
    if (k == -1)
        return;
    printPath(P, i, k);
    printf("V%d-", k + 1);
    printPath(P, k, j);
}

// 输出各个顶点之间的最短路径
void printMatrix(MGraph G, ShortPathTable D, PathMatrix P) {
    int i, j;
    for (i = 0; i < G.vexnum; i++) {
        for (j = 0; j < G.vexnum; j++) {
            if (j == i) {
                continue;
            }
            printf("V%d-V%d: 最短路径为:", i + 1, j + 1);
            if (D[i][j] == INFINITY)
                printf("%s\n", "INF");
            else {
                printf("%d", D[i][j]);
                printf("，依次经过：V%d-", i + 1);
                //调用递归函数
                printPath(P, i, j);
                printf("V%d\n", j + 1);
            }
        }
    }
}

int main() {
    MGraph G;
    PathMatrix P = { 0 };
    ShortPathTable D = { 0 };
    CreateUDG(&G);
    ShortestPath_Floyed(G, &P, &D);
    printMatrix(G, D, P);
    return 0;
}

程序中，存储带权图采用的是顺序存储结构。

实现 Floyd 算法的代码封装在 ShortestPath_Floyed() 函数中，借助了 3 个嵌套的循环结构，可以理解为：将第 k 个顶点作为 <v, w> 路径上的中间顶点。循环过程中如果发现了权值更小的路径，就将路径的权值更新到 D 数组中，将路径信息更新到 P 数组中。

输出各个顶点间最短路径的过程采用了递归的思想，感兴趣的读者可以自行研究，这里不再做重点介绍。

将图 1 中有向带权图的信息录入到程序中，执行结果为：

4,6
1 2 3 4
1,2,3
2,1,2
1,4,5
2,4,4
4,3,2
3,2,1
V1-V2: 最短路径为:3，依次经过：V1-V2
V1-V3: 最短路径为:7，依次经过：V1-V4-V3
V1-V4: 最短路径为:5，依次经过：V1-V4
V2-V1: 最短路径为:2，依次经过：V2-V1
V2-V3: 最短路径为:6，依次经过：V2-V4-V3
V2-V4: 最短路径为:4，依次经过：V2-V4
V3-V1: 最短路径为:3，依次经过：V3-V2-V1
V3-V2: 最短路径为:1，依次经过：V3-V2
V3-V4: 最短路径为:5，依次经过：V3-V2-V4
V4-V1: 最短路径为:5，依次经过：V4-V3-V2-V1
V4-V2: 最短路径为:3，依次经过：V4-V3-V2
V4-V3: 最短路径为:2，依次经过：V4-V3

总结

Floyd算法（弗洛伊德算法）专门用来查找带权图中各个顶点之间的最短路径，算法的时间复杂度可以用 O(n^3) 表示。

Floyd 算法（弗洛伊德算法）既适用于有向带权图（有向网），也适用于无向带权图（无向网）。需要注意的是，用 Floyd 算法查找最短路径，图中的权值可以是负数，但回路的权值必须是非负数，否则会导致算法查找失败。

如果想查找某个顶点到其它顶点之间的最短路径，虽然 Floyd 算法也能解决，但更推荐使用Dijkstra迪杰斯特拉算法，后者的时间复杂度为 O(n^2)。