线性表详解：一文彻底玩转线性表（万字长文，新手必看）

玩转C语言和数据结构

已于 2025-01-17 15:59:37 修改

阅读量843

点赞数 30

文章标签： c语言数据结构链表 c++ 青少年编程学习算法

于 2024-12-23 20:23:04 首次发布

版权为解学武所有，官方网站 https://xiexuewu.github.io

本文链接：https://blog.csdn.net/qq_25775935/article/details/144676438

版权

线性表是数据结构里最简单的一种存储结构，没有之一。数据结构中的很多种存储结构，包括串、广义表、树、图等，学习它们都必须有线性表的知识基础，只有玩转线性表，后续再学习复杂的存储结构才能事半功倍。

根据数据在物理内存中的存储状态，线性表又可以细分成顺序表（顺序存储结构）和链表（链式存储结构）。顺序表和链表还有很多变体，包括静态链表、循环链表、双向链表等。

这篇文章比较长，但我敢保证，大家认真看完这篇文章，就能彻底玩转线性表。

1、线性表（线性存储结构）是什么

线性表又称线性存储结构，是最简单的一种存储结构，专门用来存储逻辑关系为“一对一”的数据。

在一个数据集中，如果每个数据的左侧都有且仅有一个数据和它有关系，数据的右侧也有且仅有一个数据和它有关系，那么这些数据之间就是“一对一“的逻辑关系。

举个简单的例子：

图 1 "一对一"逻辑关系的数据

如上图所示，在 {1,2,3,4,5} 数据集中，每个数据的左侧都有且仅有一个数据和它紧挨着（除 1 外），右侧也有且仅有一个数据和它紧挨着（除 5 外），这些数据之间就是“一对一“的关系。

使用线性表存储具有“一对一“逻辑关系的数据，不仅可以将所有数据存储到内存中，还可以将“一对一”的逻辑关系也存储到内存中。

线性表存储数据的方案可以这样来理解，先用一根线将所有数据按照先后次序“串”起来，如下图所示：

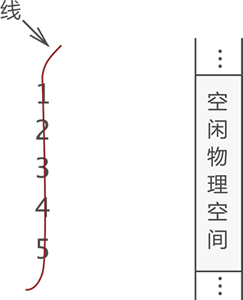
图 2 数据和“一对一”的逻辑关系

图 2 中，左侧是“串”起来的数据，右侧是空闲的物理空间。将这“一串儿”数据存放到物理空间中，有以下两种方法：

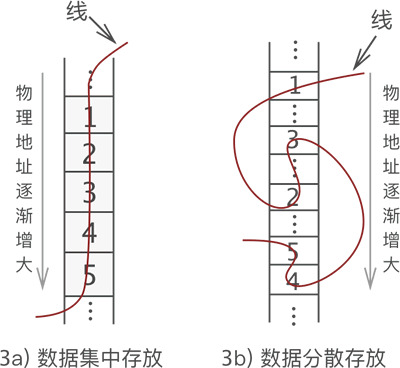
图 3 线性存储数据的方法

两种存储方式都可以将数据之间的关系存储起来，从线的一头开始捋，可以依次找到每个数据，且数据的前后位置没有发生改变。

像图 3 这样，用一根线将具有“一对一”逻辑关系的数据存储起来，这样的存储方式就称为线性表或者线性存储结构。

线性表的顺序存储和链式存储

从图 3 不难看出，线性表存储数据的实现方案有两种，分别是：

像图 3a) 那样，不破坏数据的前后次序，将它们连续存储在内存空间中，这样的存储方案称为顺序存储结构（简称顺序表顺序表顺序表）；
像图 3b) 那样，将所有数据分散存储在内存中，数据之间的逻辑关系全靠“一根线”维系，这样的存储方案称为链式存储结构（简称链表链表链表）。

也就是说，使用线性表存储数据，有两种真正可以落地的存储方案，分别是顺序表和链表。

前驱和后继

在具有“一对一“逻辑关系的数据集中，每个个体习惯称为数据元素（简称元素）。例如，图 1 显示的这组数据集中，一共有 5 个元素，分别是 1、2、3、4 和 5。

此外，很多教程中喜欢用前驱和后继来描述元素之间的前后次序：

某一元素的左侧相邻元素称为该元素的“直接前驱”，此元素左侧的所有元素统称为该元素的“前驱元素”；
某一元素的右侧相邻元素称为该元素的“直接后继”，此元素右侧的所有元素统称为该元素的“后继元素”；

以图 1 数据中的元素 3 来说，它的直接前驱是 2 ，此元素的前驱元素有 2 个，分别是 1 和 2；同理，此元素的直接后继是 4 ，后继元素也有 2 个，分别是 4 和 5。

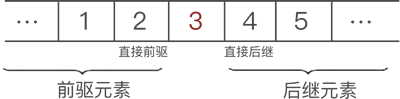
图 4 前驱和后继

2、顺序表（顺序存储结构）详解

#define Size 5 //对Size进行宏定义，表示顺序表的最大容量
void initTable(Table * t) {
    //构造一个空的顺序表，动态申请存储空间
    t->head = (int*)malloc(Size * sizeof(int));
    //如果申请失败，作出提示并直接退出程序
    if (!t->head)
    {
        printf("初始化失败");
        exit(0);
    }
    //空表的长度初始化为0
    t->length = 0;
    //空表的初始存储空间为Size
    t->size = Size;
}

如上所示，整个建立顺序表的过程都封装在一个函数中，建好的顺序表可以存储 5 个逻辑关系为“一对一”的整数。

通常情况下，malloc() 函数都可以成功申请内存空间，当申请失败时，示例程序中进行了“输出失败信息和强制程序退出”的操作，您可以根据实际需要修改代码。

顺序表的使用

通过调用 initTable() 函数，就可以成功地创建一个顺序表，还可以往顺序表中存储一些元素。

例如，将 {1,2,3,4,5} 存储到顺序表中，实现代码如下：

#include <stdio.h>
#include <stdlib.h>
#define Size 5 //对Size进行宏定义，表示顺序表的最大容量
typedef struct{
    int* head;
    int length;
    int size;
}Table;
void initTable(Table * t) {
    //构造一个空的顺序表，动态申请存储空间
    t->head = (int*)malloc(Size * sizeof(int));
    //如果申请失败，作出提示并直接退出程序
    if (!t->head)
    {
        printf("初始化失败");
        exit(0);
    }
    //空表的长度初始化为0
    t->length = 0;
    //空表的初始存储空间为Size
    t->size = Size;
}
//输出顺序表中元素的函数
void displayTable(Table t) {
    int i;
    for (i = 0; i < t.length; i++) {
        printf("%d ", t.head[i]);
    }
    printf("\n");
}
int main() {
    int i;
    Table t = { NULL,0,0 };
    initTable(&t);
    //向顺序表中添加{1,2,3,4,5}
    for (i = 1; i <= Size; i++) {
        t.head[i - 1] = i;
        t.length++;
    }
    printf("顺序表中存储的元素分别是：\n");
    displayTable(t);
    free(t.head);//释放申请的堆内存
    return 0;
}

程序运行结果如下：

顺序表中存储的元素分别是：
1 2 3 4 5

3、顺序表的基本操作（C语言实现）

我们学习了顺序表顺序表顺序表及初始化的过程，本节学习有关顺序表的一些基本操作，以及如何使用 C 语言实现它们。

顺序表插入元素

向已有顺序表中插入数据元素，根据插入位置的不同，可分为以下 3 种情况：

插入到顺序表的表头；
在表的中间位置插入元素；
尾随顺序表中已有元素，作为顺序表中的最后一个元素；

虽然数据元素插入顺序表中的位置有所不同，但是都使用的是同一种方式去解决，即：通过遍历，找到数据元素要插入的位置，然后做如下两步工作：

将要插入位置元素以及后续的元素整体向后移动一个位置；
将元素放到腾出来的位置上；

例如，在 {1,2,3,4,5} 的第 3 个位置上插入元素 6，实现过程如下：

遍历至顺序表存储第 3 个数据元素的位置，如图 1 所示：

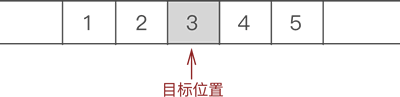
图 1 找到目标元素位置
将元素 3、4 和 5 整体向后移动一个位置，如图 2 所示：

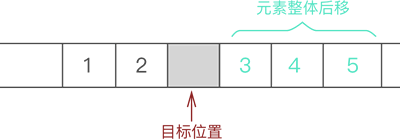
图 2 将插入位置腾出
将新元素 6 放入腾出的位置，如图 3 所示：

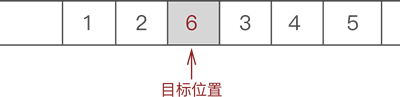
图 3 插入目标元素

因此，顺序表插入数据元素的 C 语言实现代码如下：

//插入函数，其中，elem为插入的元素，add为插入到顺序表的位置
void insertTable(Table* t, int elem, int add)
{
    int i;
    //如果插入元素位置比整张表的长度+1还大（如果相等，是尾随的情况），或者插入的位置本身不存在，程序作为提示并自动退出
    if (add > t->length + 1 || add < 1) {
        printf("插入位置有问题\n");
        return;
    }
    //做插入操作时，首先需要看顺序表是否有多余的存储空间提供给插入的元素，如果没有，需要申请
    if (t->length == t->size) {
        t->head = (int*)realloc(t->head, (t->size + 1) * sizeof(int));
        if (!t->head) {
            printf("存储分配失败\n");
            return;
        }
        t->size += 1;
    }
    //插入操作，需要将自插入位置之后的所有元素全部后移一位
    for (i = t->length - 1; i >= add - 1; i--) {
        t->head[i + 1] = t->head[i];
    }
    //后移完成后，直接插入元素
    t->head[add - 1] = elem;
    t->length++;
}

注意，动态数组数组数组额外申请更多物理空间使用的是 realloc 函数。此外在实现元素整体后移的过程中，目标位置其实是有数据的，还是 3，只是下一步新插入元素时会把旧元素直接覆盖。

顺序表删除元素

从顺序表中删除指定元素，实现起来非常简单，只需找到目标元素，并将其后续所有元素整体前移 1 个位置即可。

后续元素整体前移一个位置，会直接将目标元素删除，可间接实现删除元素的目的。

例如，从 {1,2,3,4,5} 中删除元素 3 的过程如图 4 所示：

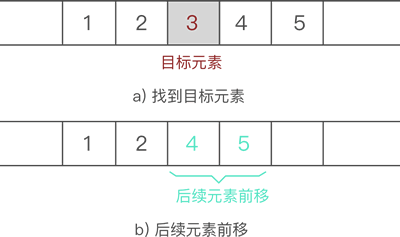
图 4 顺序表删除元素的过程示意图

因此，顺序表删除元素的 C 语言实现代码为：

void delTable(Table* t, int add) {
    int i;
    if (add > t->length || add < 1) {
        printf("被删除元素的位置有误\n");
        return;
    }
    //删除操作
    for (i = add; i < t->length; i++) {
        t->head[i - 1] = t->head[i];
    }
    t->length--;
}

顺序表查找元素

顺序表中查找目标元素，可以使用多种查找算法实现，比如说二分查找二分查找二分查找算法、插值查找算法等。

这里，我们选择顺序查找顺序查找顺序查找算法，具体实现代码为：

//查找函数，其中，elem表示要查找的数据元素的值
int selectTable(table t,int elem){
    for (int i=0; i<t.length; i++) {
        if (t.head[i]==elem) {
            return i+1;
        }
    }
    return -1;//如果查找失败，返回-1
}

顺序表更改元素

顺序表更改元素的实现过程是：

找到目标元素；
直接修改该元素的值；

顺序表更改元素的 C 语言实现代码为：

void amendTable(Table* t, int elem, int newElem) {
    int add = selectTable(*t, elem);
    if (add == -1) {
        printf("顺序表中没有找到目标元素\n");
        return;
    }
    t->head[add - 1] = newElem;
}

实例演示

以上是顺序表使用过程中最常用的基本操作，这里给出完整的实现代码：

#include <stdio.h>
#include <stdlib.h>
#define Size 5
typedef struct {
    int* head; //定义一个名为head的长度不确定的数组，也叫“动态数组”
    int length; //记录当前顺序表的长度
    int size; //记录顺序表的存储容量
}Table;
//创建顺序表
void initTable(Table* t) {
    //构造一个空的顺序表，动态申请存储空间
    t->head = (int*)malloc(Size * sizeof(int));
    //如果申请失败，作出提示并直接退出程序
    if (!t->head)
    {
        printf("初始化失败");
        exit(0);
    }
    //空表的长度初始化为0
    t->length = 0;
    //空表的初始存储空间为Size
    t->size = Size;
}
//插入函数，其中，elem为插入的元素，add为插入到顺序表的位置
void insertTable(Table* t, int elem, int add)
{
    int i;
    //如果插入元素位置比整张表的长度+1还大（如果相等，是尾随的情况），或者插入的位置本身不存在，程序作为提示并自动退出
    if (add > t->length + 1 || add < 1) {
        printf("插入位置有问题\n");
        return;
    }
    //做插入操作时，首先需要看顺序表是否有多余的存储空间提供给插入的元素，如果没有，需要申请
    if (t->length == t->size) {
        t->head = (int*)realloc(t->head, (t->size + 1) * sizeof(int));
        if (!t->head) {
            printf("存储分配失败\n");
            return;
        }
        t->size += 1;
    }
    //插入操作，需要将自插入位置之后的所有元素全部后移一位
    for (i = t->length - 1; i >= add - 1; i--) {
        t->head[i + 1] = t->head[i];
    }
    //后移完成后，直接插入元素
    t->head[add - 1] = elem;
    t->length++;
}
//删除函数
void delTable(Table* t, int add) {
    int i;
    if (add > t->length || add < 1) {
        printf("被删除元素的位置有误\n");
        return;
    }
    //删除操作
    for (i = add; i < t->length; i++) {
        t->head[i - 1] = t->head[i];
    }
    t->length--;
}
//查找函数
int selectTable(Table t, int elem) {
    int i;
    for (i = 0; i < t.length; i++) {
        if (t.head[i] == elem) {
            return i + 1;
        }
    }
    return -1;
}
//更改函数
void amendTable(Table* t, int elem, int newElem) {
    int add = selectTable(*t, elem);
    if (add == -1) {
        printf("顺序表中没有找到目标元素\n");
        return;
    }
    t->head[add - 1] = newElem;
}
//输出顺序表中的元素
void displayTable(Table t) {
    int i;
    for (i = 0; i < t.length; i++) {
        printf("%d ", t.head[i]);
    }
    printf("\n");
}
int main() {
    int i,add;
    Table t = { NULL,0,0 };
    initTable(&t);
    for (i = 1; i <= Size; i++) {
        t.head[i - 1] = i;
        t.length++;
    }
    printf("原顺序表：\n");
    displayTable(t);
    printf("删除元素1:\n");
    delTable(&t, 1);
    displayTable(t);
    printf("在第2的位置插入元素5:\n");
    insertTable(&t, 5, 2);
    displayTable(t);
    printf("查找元素3的位置:\n");
    add = selectTable(t, 3);
    printf("%d\n", add);
    printf("将元素3改为6:\n");
    amendTable(&t, 3, 6);
    displayTable(t);
    return 0;
}

程序运行结果为：

原顺序表：
1 2 3 4 5
删除元素1:
2 3 4 5
在第2的位置插入元素5:
2 5 3 4 5
查找元素3的位置:
3
将元素3改为6:
2 5 6 4 5

4、链表（单链表）是什么

链表又称单链表、链式存储结构，用于存储逻辑关系为“一对一”的数据。

和顺序表顺序表顺序表不同，使用链表存储数据，不强制要求数据在内存中集中存储，各个元素可以分散存储在内存中。例如，使用链表存储 {1,2,3}，各个元素在内存中的存储状态可能是：

图 1 数据分散存储在内存中

可以看到，数据不仅没有集中存放，在内存中的存储次序也是混乱的。那么，链表是如何存储数据间逻辑关系的呢？

链表存储数据间逻辑关系的实现方案是：为每一个元素配置一个指针，每个元素的指针都指向自己的直接后继元素，如下图所示：

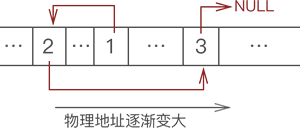
图 2 链表的实现方案

显然，我们只需要记住元素 1 的存储位置，通过它的指针就可以找到元素 2，通过元素 2 的指针就可以找到元素 3，以此类推，各个元素的先后次序一目了然。

像图 2 这样，数据元素随机存储在内存中，通过指针维系数据之间“一对一”的逻辑关系，这样的存储结构就是链表。

结点（节点）

很多教材中，也将“结点”写成“节点”，它们是一个意思。

在链表中，每个数据元素都配有一个指针，这意味着，链表上的每个“元素”都长下图这个样子：

图 3 链表中的结点结构

数据域用来存储元素的值，指针域用来存放指针。数据结构中，通常将图 3 这样的整体称为结点。

也就是说，链表中实际存放的是一个一个的结点，数据元素存放在各个结点的数据域中。举个简单的例子，图 2 中 {1,2,3} 的存储状态用链表表示，如下图所示：

图 4 链表中的结点

在 C 语言中，可以用结构体表示链表中的结点，例如：

typedef struct link{
    char elem; //代表数据域
    struct link * next; //代表指针域，指向直接后继元素
}Link;

我们习惯将结点中的指针命名为 next，因此指针域又常称为“Next 域”。

头结点、头指针和首元结点

图 4 所示的链表并不完整，一个完整的链表应该由以下几部分构成：

头指针：一个和结点类型相同的指针，它的特点是：永远指向链表中的第一个结点。上文提到过，我们需要记录链表中第一个元素的存储位置，就是用头指针实现。
结点：链表中的节点又细分为头结点、首元结点和其它结点：
- 头结点：某些场景中，为了方便解决问题，会故意在链表的开头放置一个空结点，这样的结点就称为头结点。也就是说，头结点是位于链表开头、数据域为空（不利用）的结点。
- 首元结点：指的是链表开头第一个存有数据的结点。
- 其他节点：链表中其他的节点。

也就是说，一个完整的链表是由头指针和诸多个结点构成的。每个链表都必须有头指针，但头结点不是必须的。

例如，创建一个包含头结点的链表存储 {1,2,3}，如下图所示：

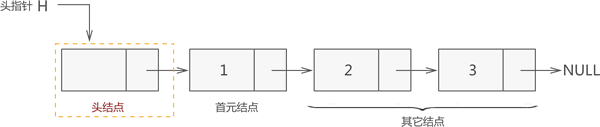
图 5 完整的链表示意图

再次强调，头指针永远指向链表中的第一个结点。换句话说，如果链表中包含头结点，那么头指针指向的是头结点，反之头指针指向首元结点。

链表的创建

创建一个链表，实现步骤如下：

定义一个头指针；
创建一个头结点或者首元结点，让头指针指向它；
每创建一个结点，都令其直接前驱结点的指针指向它。

例如，创建一个存储 {1,2,3,4} 且无头节点的链表，C 语言实现代码为：

Link* initLink() {
    int i;
    //1、创建头指针
    Link* p = NULL;
    //2、创建首元结点
    Link* temp = (Link*)malloc(sizeof(Link));
    temp->elem = 1;
    temp->next = NULL;
    //头指针指向首元结点
    p = temp;
    //3、每创建一个结点，都令其直接前驱结点的指针指向它
    for (i = 2; i < 5; i++) {
        //创建一个结点
        Link* a = (Link*)malloc(sizeof(Link));
        a->elem = i;
        a->next = NULL;
        //每次 temp 指向的结点就是 a 的直接前驱结点
        temp->next = a;
        //temp指向下一个结点（也就是a),为下次添加结点做准备
        temp = temp->next;
    }
    return p;
}

再比如，创建一个存储 {1,2,3,4} 且含头节点的链表，则 C 语言实现代码为：

Link* initLink() {
    int i;
    //1、创建头指针
    Link* p = NULL;
    //2、创建头结点
    Link* temp = (Link*)malloc(sizeof(Link));
    temp->elem = 0;
    temp->next = NULL;
    //头指针指向头结点
    p = temp;
    //3、每创建一个结点，都令其直接前驱结点的指针指向它
    for (i = 1; i < 5; i++) {
        //创建一个结点
        Link* a = (Link*)malloc(sizeof(Link));
        a->elem = i;
        a->next = NULL;
        //每次 temp 指向的结点就是 a 的直接前驱结点
        temp->next = a;
        //temp指向下一个结点（也就是a),为下次添加结点做准备
        temp = temp->next;
    }
    return p;
}

链表的使用

对于创建好的链表，我们可以依次获取链表中存储的数据，例如：

#include <stdio.h>
#include <stdlib.h>
//链表中节点的结构
typedef struct link {
    int  elem;
    struct link* next;
}Link;
Link* initLink() {
    int i;
    //1、创建头指针
    Link* p = NULL;
    //2、创建头结点
    Link* temp = (Link*)malloc(sizeof(Link));
    temp->elem = 0;
    temp->next = NULL;
    //头指针指向头结点
    p = temp;
    //3、每创建一个结点，都令其直接前驱结点的指针指向它
    for (i = 1; i < 5; i++) {
        //创建一个结点
        Link* a = (Link*)malloc(sizeof(Link));
        a->elem = i;
        a->next = NULL;
        //每次 temp 指向的结点就是 a 的直接前驱结点
        temp->next = a;
        //temp指向下一个结点（也就是a),为下次添加结点做准备
        temp = temp->next;
    }
    return p;
}
void display(Link* p) {
    Link* temp = p;//temp指针用来遍历链表
    //只要temp指向结点的next值不是NULL，就执行输出语句。
    while (temp) {
        Link* f = temp;//准备释放链表中的结点
        printf("%d ", temp->elem);
        temp = temp->next;
        free(f);
    }
    printf("\n");
}
int main() {
    Link* p = NULL;
    printf("初始化链表为：\n");
    //创建链表{1,2,3,4}
    p = initLink();
    //输出链表中的数据
    display(p);
    return 0;
}

程序中创建的是带头结点的链表，头结点的数据域存储的是元素 0，因此最终的输出结果为：

0 1 2 3 4

如果不想输出头结点的值，可以将 p->next 作为实参传递给 display() 函数。

如果程序中创建的是不带头结点的链表，最终的输出结果应该是：

1 2 3 4

5、链表的基本操作（C语言）详解

学会创建链表链表链表之后，本节继续讲解链表的一些基本操作，包括向链表中添加数据、删除链表中的数据、查找和更改链表中的数据。

首先，创建一个带头结点的链表，链表中存储着 {1,2,3,4}：

//链表中节点的结构
typedef struct link {
    int  elem;
    struct link* next;
}Link;
Link* initLink() {
    int i;
    //1、创建头指针
    Link* p = NULL;
    //2、创建头结点
    Link* temp = (Link*)malloc(sizeof(Link));
    temp->elem = 0;
    temp->next = NULL;
    //头指针指向头结点
    p = temp;
    //3、每创建一个结点，都令其直接前驱结点的指针指向它
    for (i = 1; i < 5; i++) {
        //创建一个结点
        Link* a = (Link*)malloc(sizeof(Link));
        a->elem = i;
        a->next = NULL;
        //每次 temp 指向的结点就是 a 的直接前驱结点
        temp->next = a;
        //temp指向下一个结点（也就是a),为下次添加结点做准备
        temp = temp->next;
    }
    return p;
}

链表插入元素

同顺序表顺序表顺序表一样，向链表中增添元素，根据添加位置不同，可分为以下 3 种情况：

插入到链表的头部，作为首元节点；
插入到链表中间的某个位置；
插入到链表的最末端，作为链表中最后一个结点；

对于有头结点的链表，3 种插入元素的实现思想是相同的，具体步骤是：

将新结点的 next 指针指向插入位置后的结点；
将插入位置前结点的 next 指针指向插入结点；

例如，在链表 {1,2,3,4} 的基础上分别实现在头部、中间、尾部插入新元素 5，其实现过程如图 1 所示：

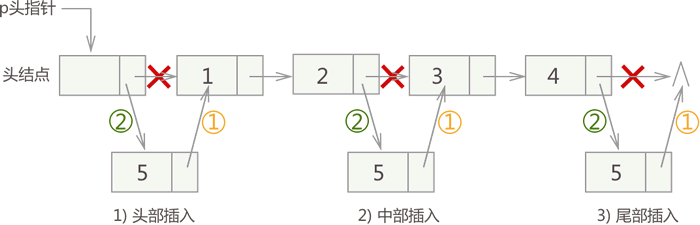
图 1 带头结点链表插入元素的 3 种情况

从图中可以看出，虽然新元素的插入位置不同，但实现插入操作的方法是一致的，都是先执行步骤 1 ，再执行步骤 2。实现代码如下：

void insertElem(Link* p, int elem, int add) {
    int i;
    Link* c = NULL;
    Link* temp = p;//创建临时结点temp
    //首先找到要插入位置的上一个结点
    for (i = 1; i < add; i++) {
        temp = temp->next;
        if (temp == NULL) {
            printf("插入位置无效\n");
            return;
        }
    }
    //创建插入结点c
    c = (Link*)malloc(sizeof(Link));
    c->elem = elem;
    //① 将新结点的 next 指针指向插入位置后的结点
    c->next = temp->next;
    //② 将插入位置前结点的 next 指针指向插入结点；
    temp->next = c;
}

注意：链表插入元素的操作必须是先步骤 1，再步骤 2；反之，若先执行步骤 2，除非再添加一个指针，作为插入位置后续链表的头指针，否则会导致插入位置后的这部分链表丢失，无法再实现步骤 1。

对于没有头结点的链表，在头部插入结点比较特殊，需要单独实现。

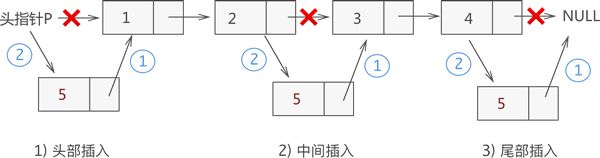
图 2 不带头结点链表插入元素的 3 种情况

和 2)、3) 种情况相比，由于链表没有头结点，在头部插入新结点，此结点之前没有任何结点，实现的步骤如下：

将新结点的指针指向首元结点；
将头指针指向新结点。

实现代码如下：

Link* insertElem(Link* p, int elem, int add) {
    if (add == 1) {
        //创建插入结点c
        Link* c = (Link*)malloc(sizeof(Link));
        c->elem = elem;
        c->next = p;
        p = c;
        return p;
    }
    else {
        int i;
        Link* c = NULL;
        Link* temp = p;//创建临时结点temp
        //首先找到要插入位置的上一个结点
        for (i = 1; i < add-1; i++) {
            temp = temp->next;
            if (temp == NULL) {
                printf("插入位置无效\n");
                return p;
            }
        }
        //创建插入结点c
        c = (Link*)malloc(sizeof(Link));
        c->elem = elem;
        //向链表中插入结点
        c->next = temp->next;
        temp->next = c;
        return p;
    }
}

注意当 add==1 成立时，形参指针 p 的值会发生变化，因此需要它的新值作为函数的返回值返回。

链表删除元素

从链表中删除指定数据元素时，实则就是将存有该数据元素的节点从链表中摘除。

对于有头结点的链表来说，无论删除头部（首元结点）、中部、尾部的结点，实现方式都一样，执行以下三步操作：

找到目标元素所在结点的直接前驱结点；
将目标结点从链表中摘下来;
手动释放结点占用的内存空间；

从链表上摘除目标节点，只需找到该节点的直接前驱节点 temp，执行如下操作：

temp->next=temp->next->next;

例如，从存有 {1,2,3,4} 的链表中删除存储元素 3 的结点，则此代码的执行效果如图 3 所示：

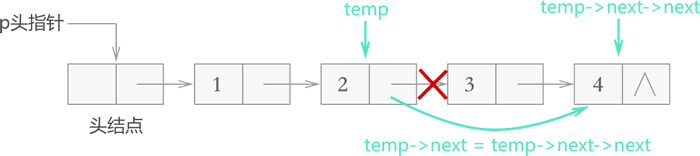
图 3 带头结点链表删除元素

实现代码如下：

//p为原链表，elem 为要删除的目标元素
int delElem(Link* p, int elem) {
    Link* del = NULL, *temp = p;
    int find = 0;
    //1、找到目标元素的直接前驱结点
    while (temp->next) {
        if (temp->next->elem == elem) {
            find = 1;
            break;
        }
        temp = temp->next;
    }
    if (find == 0) {
        return -1;//删除失败
    }
    else
    {
        //标记要删除的结点
        del = temp->next;
        //2、将目标结点从链表上摘除
        temp->next = temp->next->next;
        //3、释放目标结点
        free(del);
        return 1;
    }
}

对于不带头结点的链表，需要单独考虑删除首元结点的情况，删除其它结点的方式和图 3 完全相同，如下图所示：

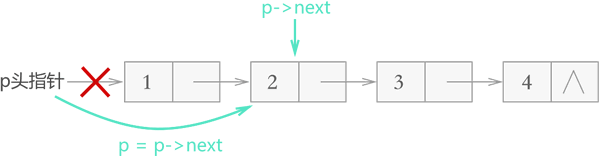
图 4 不带头结点链表删除结点

实现代码如下：

//p为原链表，elem 为要删除的目标元素
int delElem(Link** p, int elem) {
    Link* del = NULL, *temp = *p;
    //删除首元结点需要单独考虑
    if (temp->elem == elem) {
        (*p) = (*p)->next;
        free(temp);
        return 1;
    }
    else
    {
        int find = 0;
        //1、找到目标元素的直接前驱结点
        while (temp->next) {
            if (temp->next->elem == elem) {
                find = 1;
                break;
            }
            temp = temp->next;
        }
        if (find == 0) {
            return -1;//删除失败
        }
        else
        {
            //标记要删除的结点
            del = temp->next;
            //2、将目标结点从链表上摘除
            temp->next = temp->next->next;
            //3、释放目标结点
            free(del);
            return 1;
        }
    }
}

函数返回 1 时，表示删除成功；返回 -1，表示删除失败。注意，该函数的形参 p 为二级指针，调用时需要传递链表头指针的地址。

链表查找元素

在链表中查找指定数据元素，最常用的方法是：从首元结点开始依次遍历所有节点，直至找到存储目标元素的结点。如果遍历至最后一个结点仍未找到，表明链表中没有存储该元素。

因此，链表中查找特定数据元素的 C 语言实现代码为：

//p为原链表，elem表示被查找元素
int selectElem(Link* p, int elem) {
    int i = 1;
    //带头结点，p 指向首元结点
    p = p->next;
    while (p) {
        if (p->elem == elem) {
            return i;
        }
        p = p->next;
        i++;
    }
    return -1;//返回-1，表示未找到
}

注意第 5 行代码，对于有结点的链表，需要先将 p 指针指向首元结点；反之，对于不带头结点的链表，注释掉第 5 行代码即可。

链表更新元素

更新链表中的元素，只需通过遍历找到存储此元素的节点，对节点中的数据域做更改操作即可。

直接给出链表中更新数据元素的 C 语言实现代码：

//p 为有头结点的链表，oldElem 为旧元素，newElem 为新元素
int amendElem(Link* p, int oldElem, int newElem) {
    p = p->next;
    while (p) {
        if (p->elem == oldElem) {
            p->elem = newElem;
            return 1;
        }
        p = p->next;
    }
    return -1;
}

函数返回 1，表示更改成功；返回数字 -1，表示更改失败。如果是没有头结点的链表，直接删除第 3 行代码即可。

总结

以上内容详细介绍了对链表中数据元素做"增删查改"的实现过程及 C 语言代码，最后给大家一段完整的代码，实现对有头结点链表的“增删查改”：

#include <stdio.h>
#include <stdlib.h>
//链表中节点的结构
typedef struct link {
    int  elem;
    struct link* next;
}Link;
Link* initLink() {
    int i;
    //1、创建头指针
    Link* p = NULL;
    //2、创建头结点
    Link* temp = (Link*)malloc(sizeof(Link));
    temp->elem = 0;
    temp->next = NULL;
    //头指针指向头结点
    p = temp;
    //3、每创建一个结点，都令其直接前驱结点的指针指向它
    for (i = 1; i < 5; i++) {
        //创建一个结点
        Link* a = (Link*)malloc(sizeof(Link));
        a->elem = i;
        a->next = NULL;
        //每次 temp 指向的结点就是 a 的直接前驱结点
        temp->next = a;
        //temp指向下一个结点（也就是a),为下次添加结点做准备
        temp = temp->next;
    }
    return p;
}
//p为链表，elem为目标元素，add为要插入的位置
void insertElem(Link* p, int elem, int add) {
    int i;
    Link* c = NULL;
    Link* temp = p;//创建临时结点temp
    //首先找到要插入位置的上一个结点
    for (i = 1; i < add; i++) {
        temp = temp->next;
        if (temp == NULL) {
            printf("插入位置无效\n");
            return;
        }
    }
    //创建插入结点c
    c = (Link*)malloc(sizeof(Link));
    c->elem = elem;
    //① 将新结点的 next 指针指向插入位置后的结点
    c->next = temp->next;
    //② 将插入位置前结点的 next 指针指向插入结点；
    temp->next = c;
}
//p为原链表，elem 为要删除的目标元素
int delElem(Link* p, int elem) {
    Link* del = NULL, *temp = p;
    int find = 0;
    //1、找到目标元素的直接前驱结点
    while (temp->next) {
        if (temp->next->elem == elem) {
            find = 1;
            break;
        }
        temp = temp->next;
    }
    if (find == 0) {
        return -1;//删除失败
    }
    else
    {
        //标记要删除的结点
        del = temp->next;
        //2、将目标结点从链表上摘除
        temp->next = temp->next->next;
        //3、释放目标结点
        free(del);
        return 1;
    }
}
//p为原链表，elem表示被查找元素
int selectElem(Link* p, int elem) {
    int i = 1;
    //带头结点，p 指向首元结点
    p = p->next;
    while (p) {
        if (p->elem == elem) {
            return i;
        }
        p = p->next;
        i++;
    }
    return -1;//返回-1，表示未找到
}
//p 为有头结点的链表，oldElem 为旧元素，newElem 为新元素
int amendElem(Link* p, int oldElem, int newElem) {
    p = p->next;
    while (p) {
        if (p->elem == oldElem) {
            p->elem = newElem;
            return 1;
        }
        p = p->next;
    }
    return -1;
}
//输出链表中各个结点的元素
void display(Link* p) {
    p = p->next;
    while (p) {
        printf("%d ", p->elem);
        p = p->next;
    }
    printf("\n");
}
//释放链表
void Link_free(Link* p) {
    Link* fr = NULL;
    while (p->next)
    {
        fr = p->next;
        p->next = p->next->next;
        free(fr);
    }
    free(p);
}
int main() {
    Link* p = initLink();
    printf("初始化链表为：\n");
    display(p);
    printf("在第 3 的位置上添加元素 6：\n");
    insertElem(p, 6, 3);
    display(p);
    printf("删除元素4：\n");
    delElem(p, 4);
    display(p);
    printf("查找元素 2：\n");
    printf("元素 2 的位置为：%d\n", selectElem(p, 2));
    printf("更改元素 1 的值为 6：\n");
    amendElem(p, 1, 6);
    display(p);
    Link_free(p);
    return 0;
}

执行结果为：

初始化链表为：
1 2 3 4
在第 3 的位置上添加元素 6：
1 2 6 3 4
删除元素4：
1 2 6 3
查找元素 2：
元素 2 的位置为：2
更改元素 1 的值为 6：
6 2 6 3

6、静态链表及实现（C语言）详解

我们了解了顺序表和链表各自的特点，那么，是否存在一种存储结构，可以融合顺序表
和链表
各自的优点，从而既能快速访问元素，又能快速增加或删除数据元素。

静态链表，也是线性存储结构的一种，它兼顾了顺序表和链表的优点于一身，可以看做是顺序表和链表的升级版。

使用静态链表存储数据，数据全部存储在数组
中（和顺序表一样），但存储位置是随机的，数据之间"一对一"的逻辑关系通过一个整形变量（称为"游标"，和指针功能类似）维持（和链表类似）。

例如，使用静态链表存储 {1,2,3} 的过程如下：

创建一个足够大的数组，假设大小为 6，如图
1 所示：

空数组

图 1 空数组

接着，在将数据存放到数组中时，给各个数据元素配备一个整形变量，此变量用于指明各个元素的直接后继元素所在数组中的位置下标，如图 2 所示：

静态链表存储数据

图 2 静态链表存储数据

通常，静态链表会将第一个数据元素放到数组下标为 1 的位置（a[1]）中。

图 2 中，从 a[1] 存储的数据元素 1 开始，通过存储的游标变量 3，就可以在 a[3] 中找到元素 1 的直接后继元素 2；同样，通过元素 a[3] 存储的游标变量 5，可以在 a[5] 中找到元素 2 的直接后继元素 3，这样的循环过程直到某元素的游标变量为 0 截止（因为 a[0] 默认不存储数据元素）。

类似图 2 这样，通过 "数组+游标" 的方式存储具有线性关系数据的存储结构就是静态链表。

静态链表中的节点

通过上面的学习我们知道，静态链表存储数据元素也需要自定义数据类型，至少需要包含以下 2 部分信息：

数据域：用于存储数据元素的值；
游标：其实就是数组下标，表示直接后继元素所在数组中的位置；

因此，静态链表中节点的构成用 C 语言实现为：

typedef struct {

    int data;//数据域

    int cur;//游标

}component;

备用链表

图 2 显示的静态链表还不够完整，静态链表中，除了数据本身通过游标组成的链表外，还需要有一条连接各个空闲位置的链表，称为备用链表。

备用链表的作用是回收数组中未使用或之前使用过（目前未使用）的存储空间，留待后期使用。也就是说，静态链表使用数组申请的物理空间中，存有两个链表，一条连接数据，另一条连接数组中未使用的空间。

通常，备用链表的表头位于数组下标为 0（a[0]）的位置，而数据链表的表头位于数组下标为 1（a[1]）的位置。

静态链表中设置备用链表的好处是，可以清楚地知道数组中是否有空闲位置，以便数据链表添加新数据时使用。比如，若静态链表中数组下标为 0 的位置上存有数据，则证明数组已满。

例如，使用静态链表存储 {1,2,3}，假设使用长度为 6 的数组 a，则存储状态可能如图 3 所示：

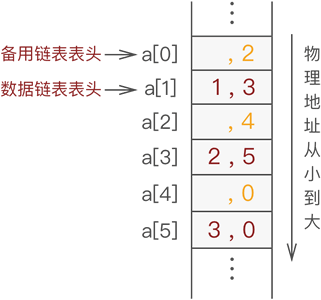
备用链表和数据链表

图 3 备用链表和数据链表

图 3 中，备用链表上连接的依次是 a[0]、a[2] 和 a[4]，而数据链表上连接的依次是 a[1]、a[3] 和 a[5]。

静态链表的实现

假设使用静态链表（数组长度为 6）存储 {1,2,3}，则需经历以下几个阶段。

在数据链表未初始化之前，数组中所有位置都处于空闲状态，因此都应被链接在备用链表上，如图 4 所示：

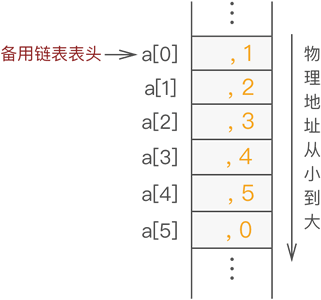
未存储数据之前静态链表的状态

图 4 未存储数据之前静态链表的状态

当向静态链表中添加数据时，需提前从备用链表中摘除节点，以供新数据使用。

备用链表摘除节点最简单的方法是摘除 a[0] 的直接后继节点；同样，向备用链表中添加空闲节点也是添加作为 a[0] 新的直接后继节点。因为 a[0] 是备用链表的第一个节点，我们知道它的位置，操作它的直接后继节点相对容易，无需遍历备用链表，耗费的时间复杂度
为 O(1)。

因此，在图 4 的基础上，向静态链表中添加元素 1 的过程如图 5 所示：

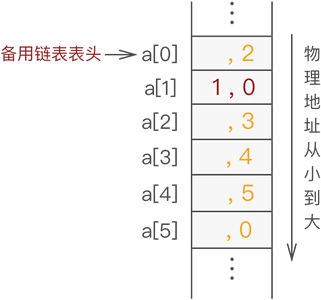
静态链表中添加元素 1

图 5 静态链表中添加元素 1

在图 5 的基础上，添加元素 2 的过程如图 6 所示：

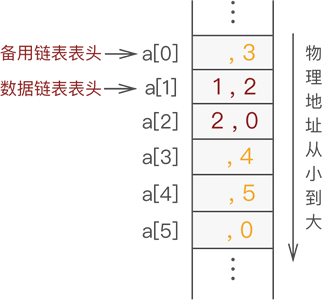
静态链表中继续添加元素 2

图 6 静态链表中继续添加元素 2

在图 6 的基础上，继续添加元素 3 ，过程如图 7 所示：

静态链表中继续添加元素 3

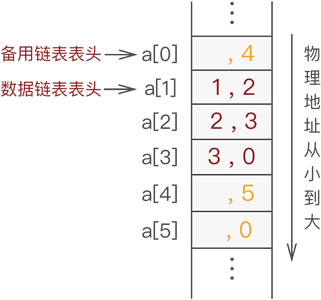
图 7 静态链表中继续添加元素 3

由此，静态链表就创建完成了。

下面给出了创建静态链表的 C 语言实现代码：

#include <stdio.h>
#define maxSize 6
typedef struct {
    int data;
    int cur;
}component;
//将结构体数组中所有分量链接到备用链表中
void reserveArr(component *array);
//初始化静态链表
int initArr(component *array);
//输出函数
void displayArr(component * array, int body);
//从备用链表上摘下空闲节点的函数
int mallocArr(component * array);
int main() {
    component array[maxSize];
    int body = initArr(array);
    printf("静态链表为：\n");
    displayArr(array, body);
    return 0;
}
//创建备用链表
void reserveArr(component *array) {
    int i = 0;
    for (i = 0; i < maxSize; i++) {
        array[i].cur = i + 1;//将每个数组分量链接到一起
        array[i].data = 0;
    }
    array[maxSize - 1].cur = 0;//链表最后一个结点的游标值为0
}
//提取分配空间
int mallocArr(component * array) {
    //若备用链表非空，则返回分配的结点下标，否则返回 0（当分配最后一个结点时，该结点的游标值为 0）
    int i = array[0].cur;
    if (array[0].cur) {
        array[0].cur = array[i].cur;
    }
    return i;
}
//初始化静态链表
int initArr(component *array) {
    int tempBody = 0, body = 0;
    int i = 0;
    reserveArr(array);
    body = mallocArr(array);
    //建立首元结点
    array[body].data = 1;
    array[body].cur = 0;
    //声明一个变量，把它当指针使，指向链表的最后的一个结点，当前和首元结点重合
    tempBody = body;
    for (i = 2; i < 4; i++) {
        int j = mallocArr(array); //从备用链表中拿出空闲的分量
        array[j].data = i;      //初始化新得到的空间结点
        array[tempBody].cur = j; //将新得到的结点链接到数据链表的尾部
        tempBody = j;             //将指向链表最后一个结点的指针后移
    }
    array[tempBody].cur = 0;//新的链表最后一个结点的指针设置为0
    return body;
}
void displayArr(component * array, int body) {
    int tempBody = body;//tempBody准备做遍历使用
    while (array[tempBody].cur) {
        printf("%d,%d\n", array[tempBody].data, array[tempBody].cur);
        tempBody = array[tempBody].cur;
    }
    printf("%d,%d\n", array[tempBody].data, array[tempBody].cur);
}

代码输出结果为：

静态链表为：
1,2
2,3
3,0

由此，我们就成功创建了一个不带头结点的静态链表（如图 7 所示），感兴趣的读者可自行尝试创建一个带有头结点的静态链表。

7、静态链表基本操作（C语言实现）

上节，我们初步创建了一个静态链表
，本节学习有关静态链表
的一些基本操作，包括对表中数据元素的添加、删除、查找和更改。

本节是建立在已成功创建静态链表的基础上，我们继续使用上节中建立好的静态链表学习本节内容，建立好的静态链表如图
1 所示：

建立好的静态链表

图 1 建立好的静态链表

可以看到，静态链表中存储的是无头结点的单链表。

静态链表添加元素

例如，在图 1 的基础，将元素 4 添加到静态链表中的第 3 个位置上，实现过程如下：

从备用链表中摘除一个节点，用于存储元素 4；
找到表中第 2 个节点（添加位置的前一个节点，这里是数据元素 2），将元素 2 的游标赋值给新元素 4；
将元素 4 所在数组
中的下标赋值给元素 2 的游标；

经过以上几步操作，数据元素 4 就成功地添加到了静态链表中，此时新的静态链表如图 2 所示：

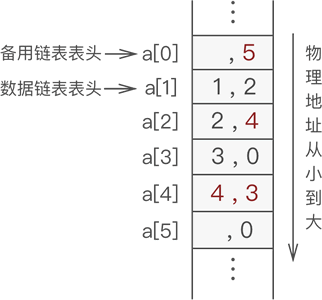
图 2 添加元素 4 的静态链表

由此，我们通过尝试编写 C 语言程序实现以上操作。读者可参考如下程序：

//向链表中插入数据，body表示链表的头结点在数组中的位置，add表示插入元素的位置，num表示要插入的数据
int insertArr(component* array, int body, int add, int num) {
    int tempBody = body;//tempBody做遍历结构体数组使用
    int i = 0, insert = 0;
    insert = mallocArr(array);//申请空间，准备插入
    array[insert].data = num;
    //对于无头结点的链表，插入到头部需要特殊考虑
    if (add == 1) {
        array[insert].cur = body;
        body = insert;
    }
    //插入到除链表头的其它位置
    else
    {
        //找到要插入位置的上一个结点在数组中的位置
        for (i = 1; i < add - 1; i++) {
            tempBody = array[tempBody].cur;
        }
        array[insert].cur = array[tempBody].cur;//新插入结点的游标等于其直接前驱结点的游标
        array[tempBody].cur = insert;//直接前驱结点的游标等于新插入结点所在数组中的下标 
    }
    return body;
}

静态链表删除元素

静态链表中删除指定元素，只需实现以下 2 步操作：

将存有目标元素的节点从数据链表中摘除；
将摘除节点添加到备用链表，以便下次再用；

比较特殊的是，对于无头结点的数据链表来说，如果需要删除头结点，则势必会导致数据链表的表头不再位于数组下标为 1 的位置，换句话说，删除头结点之后，原数据链表中第二个结点将作为整个链表新的首元结点。

若问题中涉及大量删除元素的操作，建议读者在建立静态链表之初创建一个带有头节点的静态链表，方便实现删除链表中第一个数据元素的操作。

如下是针对无头结点的数据链表，实现删除操作的 C 语言代码：

//删除结点函数，num表示被删除结点中数据域存放的数据，函数返回新数据链表的表头位置
int deletArr(component * array, int body, int num) {
    int tempBody = body;
    int del = 0;
    int newbody = 0;
    //找到被删除结点的位置
    while (array[tempBody].data != num) {
        tempBody = array[tempBody].cur;
        //当tempBody为0时，表示链表遍历结束，说明链表中没有存储该数据的结点
        if (tempBody == 0) {
            printf("链表中没有此数据");
            return;
        }
    }
    //运行到此，证明有该结点
    del = tempBody;
    tempBody = body;
    //删除首元结点，需要特殊考虑
    if (del == body) {
        newbody = array[del].cur;
        freeArr(array, del);
        return newbody;
    }
    else
    {
        //找到该结点的上一个结点，做删除操作
        while (array[tempBody].cur != del) {
            tempBody = array[tempBody].cur;
        }
        //将被删除结点的游标直接给被删除结点的上一个结点
        array[tempBody].cur = array[del].cur;
        //回收被摘除节点的空间
        freeArr(array, del);
        return body;
    }  
}

静态链表查找元素

静态链表查找指定元素，由于我们只知道静态链表第一个元素所在数组中的位置，因此只能通过逐个遍历静态链表的方式，查找存有指定数据元素的节点。

静态链表查找指定数据元素的 C 语言实现代码如下：

//在以body作为头结点的链表中查找数据域为elem的结点在数组中的位置
int selectNum(component * array, int body, int num) {
    //当游标值为0时，表示链表结束
    while (array[body].cur != 0) {
        if (array[body].data == num) {
            return body;
        }
        body = array[body].cur;
    }
    //判断最后一个结点是否符合要求
    if (array[body].data == num) {
        return body;
    }
    return -1;//返回-1，表示在链表中没有找到该元素
}

静态链表中更改数据

更改静态链表中的数据，只需找到目标元素所在的节点，直接更改节点中的数据域即可。

实现此操作的 C 语言代码如下：

//在以body作为头结点的链表中将数据域为oldElem的结点，数据域改为newElem
void amendElem(component * array, int body, int oldElem, int newElem) {
    int add = selectNum(array, body, oldElem);
    if (add == -1) {
        printf("无更改元素");
        return;
    }
    array[add].data = newElem;
}

总结

这里给出以上对静态链表做 "增删查改" 操作的完整实现代码：

#include <stdio.h>
#define maxSize 7
typedef struct {
    int data;
    int cur;
}component;
//将结构体数组中所有分量链接到备用链表中
void reserveArr(component* array);
//初始化静态链表
int initArr(component* array);
//向链表中插入数据，body表示链表的头结点在数组中的位置，add表示插入元素的位置，num表示要插入的数据
int insertArr(component* array, int body, int add, int num);
//删除链表中存有num的结点,返回新数据链表中第一个节点所在的位置
int deletArr(component* array, int body, int num);
//查找存储有num的结点在数组的位置
int selectNum(component* array, int body, int num);
//将链表中的字符oldElem改为newElem
void amendElem(component* array, int body, int oldElem, int newElem);
//输出函数
void displayArr(component* array, int body);
//从备用链表中摘除空闲节点的实现函数
int mallocArr(component* array);
//将摘除下来的节点链接到备用链表上
void freeArr(component* array, int k);

int main() {
    component array[maxSize];
    int body = initArr(array);
    int selectAdd;
    printf("静态链表为：\n");
    displayArr(array, body);

    printf("在第3的位置上插入元素4:\n");
    body = insertArr(array, body, 3, 4);
    displayArr(array, body);

    printf("删除数据域为1的结点:\n");
    body = deletArr(array, body, 1);
    displayArr(array, body);

    printf("查找数据域为4的结点的位置:\n");
    selectAdd = selectNum(array, body, 4);
    printf("%d\n", selectAdd);
    printf("将结点数据域为4改为5:\n");
    amendElem(array, body, 4, 5);
    displayArr(array, body);
    return 0;
}

//提取分配空间
int mallocArr(component* array) {
    //若备用链表非空，则返回分配的结点下标，否则返回0（当分配最后一个结点时，该结点的游标值为0）
    int i = array[0].cur;
    if (array[0].cur) {
        array[0].cur = array[i].cur;
    }
    return i;
}

//创建备用链表
void reserveArr(component* array) {
    int i = 0;
    for (i = 0; i < maxSize; i++) {
        array[i].cur = i + 1;//将每个数组分量链接到一起
    }
    array[maxSize - 1].cur = 0;//链表最后一个结点的游标值为0
}

//初始化静态链表
int initArr(component* array) {
    int tempBody = 0, body = 0;
    int i = 0;
    reserveArr(array);
    body = mallocArr(array);
    //建立首元结点
    array[body].data = 1;
    array[body].cur = 0;
    //声明一个变量，把它当指针使，指向链表的最后的一个结点，当前和首元结点重合
    tempBody = body;
    for (i = 2; i < 4; i++) {
        int j = mallocArr(array); //从备用链表中拿出空闲的分量
        array[j].data = i;      //初始化新得到的空间结点
        array[tempBody].cur = j; //将新得到的结点链接到数据链表的尾部
        tempBody = j;             //将指向链表最后一个结点的指针后移
    }
    array[tempBody].cur = 0;//新的链表最后一个结点的指针设置为0
    return body;
}

//向链表中插入数据，body表示链表的头结点在数组中的位置，add表示插入元素的位置，num表示要插入的数据
int insertArr(component* array, int body, int add, int num) {
    int tempBody = body;//tempBody做遍历结构体数组使用
    int i = 0, insert = 0;

    insert = mallocArr(array);//申请空间，准备插入
    array[insert].data = num;
    //对于无头结点的链表，插入到头部需要特殊考虑
    if (add == 1) {
        array[insert].cur = body;
        body = insert;
    }
    //插入到除链表头的其它位置
    else
    {
        //找到要插入位置的上一个结点在数组中的位置
        for (i = 1; i < add - 1; i++) {
            tempBody = array[tempBody].cur;
        }
        array[insert].cur = array[tempBody].cur;//新插入结点的游标等于其直接前驱结点的游标
        array[tempBody].cur = insert;//直接前驱结点的游标等于新插入结点所在数组中的下标 
    }
    return body;
}

//删除结点函数，num表示被删除结点中数据域存放的数据
int deletArr(component* array, int body, int num) {
    int tempBody = body;
    int del = 0;
    int newbody = 0;
    //找到被删除结点的位置
    while (array[tempBody].data != num) {
        tempBody = array[tempBody].cur;
        //当tempBody为0时，表示链表遍历结束，说明链表中没有存储该数据的结点
        if (tempBody == 0) {
            printf("链表中没有此数据");
            return;
        }
    }
    //运行到此，证明有该结点
    del = tempBody;
    tempBody = body;
    //删除首元结点，需要特殊考虑
    if (del == body) {
        newbody = array[del].cur;
        freeArr(array, del);
        return newbody;
    }
    else
    {
        //找到该结点的上一个结点，做删除操作
        while (array[tempBody].cur != del) {
            tempBody = array[tempBody].cur;
        }
        //将被删除结点的游标直接给被删除结点的上一个结点
        array[tempBody].cur = array[del].cur;
        //回收被摘除节点的空间
        freeArr(array, del);
        return body;
    }
}

//在以body作为头结点的链表中查找数据域为elem的结点在数组中的位置
int selectNum(component* array, int body, int num) {
    //当游标值为0时，表示链表结束
    while (array[body].cur != 0) {
        if (array[body].data == num) {
            return body;
        }
        body = array[body].cur;
    }
    //判断最后一个结点是否符合要求
    if (array[body].data == num) {
        return body;
    }
    return -1;//返回-1，表示在链表中没有找到该元素
}

//在以body作为头结点的链表中将数据域为oldElem的结点，数据域改为newElem
void amendElem(component* array, int body, int oldElem, int newElem) {
    int add = selectNum(array, body, oldElem);
    if (add == -1) {
        printf("无更改元素");
        return;
    }
    array[add].data = newElem;
}

void displayArr(component* array, int body) {
    int tempBody = body;//tempBody准备做遍历使用
    while (array[tempBody].cur) {
        printf("%d,%d ", array[tempBody].data, array[tempBody].cur);
        tempBody = array[tempBody].cur;
    }
    printf("%d,%d\n", array[tempBody].data, array[tempBody].cur);
}

//备用链表回收空间的函数，其中array为存储数据的数组，k表示未使用节点所在数组的下标
void freeArr(component* array, int k) {
    array[k].cur = array[0].cur;
    array[0].cur = k;
}

程序运行结果为：

静态链表为：
1,2 2,3 3,0
在第3的位置上插入元素4:
1,2 2,4 4,3 3,0
删除数据域为1的结点:
2,4 4,3 3,0
查找数据域为4的结点的位置:
4
将结点数据域为4改为5:
2,4 5,3 3,0

8、双向链表详解（C语言实现）

目前我们所学到的链表
，无论是动态链表还是静态链表
，表中各个节点都只包含一个指针（游标），且都统一指向直接后继节点，这类链表又统称为单向链表或单链表。

虽然单链表能 100% 存储逻辑关系为 "一对一" 的数据，但在解决某些实际问题时，单链表的执行效率并不高。例如，若实际问题中需要频繁地查找某个结点的前驱结点，使用单链表存储数据显然没有优势，因为单链表的强项是从前往后查找目标元素，不擅长从后往前查找元素。

解决此类问题，可以建立双向链表（简称双链表）。

双向链表是什么

从名字上理解双向链表，即链表是 "双向" 的，如图
1 所示：

双向链表结构示意图

图 1 双向链表结构示意图

“双向”指的是各节点之间的逻辑关系是双向的，头指针通常只设置一个。

从图 1 中可以看到，双向链表中各节点包含以下 3 部分信息（如图 2 所示）：

指针域：用于指向当前节点的直接前驱节点；
数据域：用于存储数据元素。
指针域：用于指向当前节点的直接后继节点；

双向链表的节点构成

图 2 双向链表的节点构成

因此，双链表的节点结构用 C 语言实现为：

typedef struct line{
    struct line * prior; //指向直接前趋
    int data;
    struct line * next; //指向直接后继
}Line;

双向链表的创建

同单链表相比，双链表仅是各节点多了一个用于指向直接前驱的指针域。因此，我们可以在单链表的基础轻松实现对双链表的创建。

需要注意的是，与单链表不同，双链表创建过程中，每创建一个新节点都要与其前驱节点建立两次联系，分别是：

将新节点的 prior 指针指向直接前驱节点；
将直接前驱节点的 next 指针指向新节点；

这里给出创建双向链表的 C 语言实现代码：

Line* initLine(Line* head) {
    Line* list = NULL;
    head = (Line*)malloc(sizeof(Line));//创建链表第一个结点（首元结点）
    head->prior = NULL;
    head->next = NULL;
    head->data = 1;
    list = head;
    for (int i = 2; i <= 5; i++) {
        //创建并初始化一个新结点
        Line* body = (Line*)malloc(sizeof(Line));
        body->prior = NULL;
        body->next = NULL;
        body->data = i;
        //直接前趋结点的next指针指向新结点
        list->next = body;
        //新结点指向直接前趋结点
        body->prior = list;
        list = list->next;
    }
    return head;
}

我们可以尝试着在 main 函数中输出创建的双链表，C 语言代码如下：

#include <stdio.h>
#include <stdlib.h>
typedef struct line {
    struct line* prior; //指向直接前趋
    int data;
    struct line* next; //指向直接后继
}Line;

Line* initLine(Line* head) {
    int i;
    Line* list = NULL;
    head = (Line*)malloc(sizeof(Line));//创建链表第一个结点（首元结点）
    head->prior = NULL;
    head->next = NULL;
    head->data = 1;
    list = head;
    for (i = 2; i <= 5; i++) {
        //创建并初始化一个新结点
        Line* body = (Line*)malloc(sizeof(Line));
        body->prior = NULL;
        body->next = NULL;
        body->data = i;
        //直接前趋结点的next指针指向新结点
        list->next = body;
        //新结点指向直接前趋结点
        body->prior = list;
        list = list->next;
    }
    return head;
}
//输出链表中的数据
void display(Line* head) {
    Line* temp = head;
    while (temp) {
        //如果该节点无后继节点，说明此节点是链表的最后一个节点
        if (temp->next == NULL) {
            printf("%d\n", temp->data);
        }
        else {
            printf("%d <-> ", temp->data);
        }
        temp = temp->next;
    }
}
//释放链表中结点占用的空间
void free_line(Line* head) {
    Line* temp = head;
    while (temp) {
        head = head->next;
        free(temp);
        temp = head;
    }
}

int main()
{
    //创建一个头指针
    Line* head = NULL;
    //调用链表创建函数
    head = initLine(head);
    //输出创建好的链表
    display(head);
    //显示双链表的优点
    printf("链表中第 4 个节点的直接前驱是：%d", head->next->next->next->prior->data);
    free_line(head);
    return 0;
}

程序运行结果：

1 <-> 2 <-> 3 <-> 4 <-> 5
链表中第 4 个节点的直接前驱是：3

9、双向链表基本操作（C语言实现）

前面学习了如何创建一个双向链表
，本节学习有关双向链表
的一些基本操作，即如何在双向链表中添加、删除、查找或更改数据元素。

本节知识基于已熟练掌握双向链表创建过程的基础上，我们继续上节所创建的双向链表来学习本节内容，创建好的双向链表如图
1 所示：

双向链表示意图

图 1 双向链表示意图

双向链表添加节点

根据数据添加到双向链表中的位置不同，可细分为以下 3 种情况：

1) 添加至表头

将新数据元素添加到表头，只需要将该元素与表头元素建立双层逻辑关系即可。

换句话说，假设新元素节点为 temp，表头节点为 head，则需要做以下 2 步操作即可：

temp->next=head; head->prior=temp;
将 head 移至 temp，重新指向新的表头；

例如，将新元素 7 添加至双链表的表头，则实现过程如图 2 所示：

添加元素至双向链表的表头

图 2 添加元素至双向链表的表头

2) 添加至表的中间位置

同单链表添加数据类似，双向链表中间位置添加数据需要经过以下 2 个步骤，如图 3 所示：

新节点先与其直接后继节点建立双层逻辑关系；
新节点的直接前驱节点与之建立双层逻辑关系；

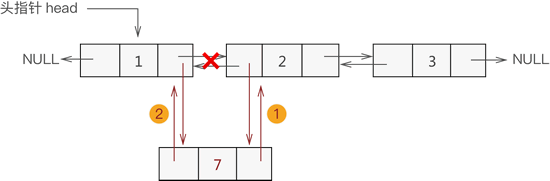
双向链表中间位置添加数据元素

图 3 双向链表中间位置添加数据元素

3) 添加至表尾

与添加到表头是一个道理，实现过程如下（如图 4 所示）：

找到双链表中最后一个节点；
让新节点与最后一个节点进行双层逻辑关系；

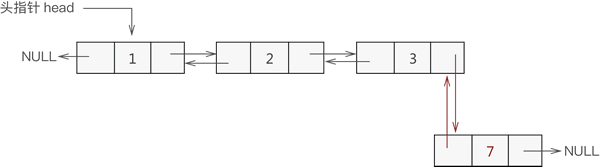
双向链表尾部添加数据元素

图 4 双向链表尾部添加数据元素

因此，我们可以试着编写双向链表添加数据的 C 语言代码，参考代码如下：

Line* insertLine(Line* head, int data, int add) {
    //新建数据域为data的结点
    Line* temp = (Line*)malloc(sizeof(Line));
    temp->data = data;
    temp->prior = NULL;
    temp->next = NULL;
    //插入到链表头，要特殊考虑
    if (add == 1) {
        temp->next = head;
        head->prior = temp;
        head = temp;
    }
    else {
        int i;
        Line* body = head;
        //找到要插入位置的前一个结点
        for (i = 1; i < add - 1; i++) {
            body = body->next;
            //只要 body 不存在，表明插入位置输入错误
            if (!body) {
                printf("插入位置有误！\n");
                return head;
            }
        }
        //判断条件为真，说明插入位置为链表尾，实现第 2 种情况
        if (body && (body->next == NULL)) {
            body->next = temp;
            temp->prior = body;
        }
        else {
            //第 2 种情况的具体实现
            body->next->prior = temp;
            temp->next = body->next;
            body->next = temp;
            temp->prior = body;
        }
    }
    return head;
}

双向链表删除节点

和添加结点的思想类似，在双向链表中删除目标结点也分为 3 种情况。

1) 删除表头结点

删除表头结点的过程如下图所示：

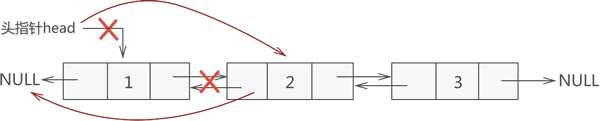
图 5 删除双链表表头元素

删除表头结点的实现过程是：

新建一个指针指向表头结点；
断开表头结点和其直接后续结点之间的关联，更改 head 头指针的指向，同时将其直接后续结点的 prior 指针指向 NULL；
释放表头结点占用的内存空间。

2) 删除表中结点

删除表中结点的过程如下图所示：

双链表删除元素操作示意图

图 6 删除表中结点

删除表中结点的实现过程是：

找到目标结点，新建一个指针指向改结点；
将目标结点从链表上摘除；
释放该结点占用的内存空间。

3) 删除表尾结点

删除表尾结点的过程如下图所示：

图 7 删除表尾结点

删除表尾结点的实现过程是：

找到表尾结点，新建一个指针指向该结点；
断点表尾结点和其直接前驱结点的关联，并将其直接前驱结点的 next 指针指向 NULL；
释放表尾结点占用的内存空间。

双向链表删除节点的 C 语言实现代码如下：

//删除结点的函数，data为要删除结点的数据域的值
Line* delLine(Line* head, int data) {
    Line* temp = head;
    while (temp) {
        if (temp->data == data) {
            //删除表头结点
            if (temp->prior == NULL) {
                head = head->next;
                if (head) {
                    head->prior = NULL;
                    temp->next = NULL;
                }
                free(temp);
                return head;
            }
            //删除表中结点
            if (temp->prior && temp->next) {
                temp->next->prior = temp->prior;
                temp->prior->next = temp->next;
                free(temp);
                return head;
            }
            //删除表尾结点
            if (temp->next == NULL) {
                temp->prior->next = NULL;
                temp->prior = NULL;
                free(temp);
                return head;
            }
        }
        temp = temp->next;
    }
    printf("表中没有目标元素，删除失败\n");
    return head;
}

双向链表查找节点

通常情况下，双向链表和单链表一样都仅有一个头指针。因此，双链表查找指定元素的实现同单链表类似，也是从表头依次遍历表中元素。

C 语言实现代码为：

//head为原双链表，elem表示被查找元素
int selectElem(line * head,int elem){
//新建一个指针t，初始化为头指针 head
    line * t=head;
    int i=1;
    while (t) {
        if (t->data==elem) {
            return i;
        }
        i++;
        t=t->next;
    }
    //程序执行至此处，表示查找失败
    return -1;
}

双向链表更改节点

更改双链表中指定结点数据域的操作是在查找的基础上完成的。实现过程是：通过遍历找到存储有该数据元素的结点，直接更改其数据域即可。

实现此操作的 C 语言实现代码如下：

//更新函数，其中，add 表示要修改的元素，newElem 为新数据的值
void amendElem(Line* p, int oldElem, int newElem) {
    Line* temp = p;
    int find = 0;
    //找到要修改的目标结点
    while (temp)
    {
        if (temp->data == oldElem) {
            find = 1;
            break;
        }
        temp = temp->next;
    }
    //成功找到，则进行更改操作
    if (find == 1) {
        temp->data = newElem;
        return;
    }
    //查找失败，输出提示信息
    printf("链表中未找到目标元素，更改失败\n");
}

总结

这里给出双链表中对数据进行 "增删查改" 操作的完整实现代码：

#include <stdio.h>
#include <stdlib.h>
typedef struct line {
    struct line* prior; //指向直接前趋
    int data;
    struct line* next; //指向直接后继
}Line;

Line* initLine(Line* head) {
    int i;
    Line* list = NULL;
    head = (Line*)malloc(sizeof(Line));//创建链表第一个结点（首元结点）
    head->prior = NULL;
    head->next = NULL;
    head->data = 1;
    list = head;
    for (i = 2; i <= 5; i++) {
        //创建并初始化一个新结点
        Line* body = (Line*)malloc(sizeof(Line));
        body->prior = NULL;
        body->next = NULL;
        body->data = i;
        //直接前趋结点的next指针指向新结点
        list->next = body;
        //新结点指向直接前趋结点
        body->prior = list;
        list = list->next;
    }
    return head;
}

void display(Line* head) {
    Line* temp = head;
    while (temp) {
        //如果该节点无后继节点，说明此节点是链表的最后一个节点
        if (temp->next == NULL) {
            printf("%d\n", temp->data);
        }
        else {
            printf("%d <-> ", temp->data);
        }
        temp = temp->next;
    }
}

//删除结点的函数，data为要删除结点的数据域的值
Line* delLine(Line* head, int data) {
    Line* temp = head;
    while (temp) {
        if (temp->data == data) {
            //删除表头结点
            if (temp->prior == NULL) {
                head = head->next;
                if (head) {
                    head->prior = NULL;
                    temp->next = NULL;
                }
                free(temp);
                return head;
            }
            //删除表中结点
            if (temp->prior && temp->next) {
                temp->next->prior = temp->prior;
                temp->prior->next = temp->next;
                free(temp);
                return head;
            }
            //删除表尾结点
            if (temp->next == NULL) {
                temp->prior->next = NULL;
                temp->prior = NULL;
                free(temp);
                return head;
            }
        }
        temp = temp->next;
    }
    printf("表中没有目标元素，删除失败\n");
    return head;
}

//head为原双链表，elem表示被查找元素
int selectElem(Line* head, int elem) {
    //新建一个指针t，初始化为头指针 head
    Line* t = head;
    int i = 1;
    while (t) {
        if (t->data == elem) {
            return i;
        }
        i++;
        t = t->next;
    }
    //程序执行至此处，表示查找失败
    return -1;
}

//更新函数，其中，add 表示要修改的元素，newElem 为新数据的值
void amendElem(Line* p, int oldElem, int newElem) {
    Line* temp = p;
    int find = 0;
    //找到要修改的目标结点
    while (temp)
    {
        if (temp->data == oldElem) {
            find = 1;
            break;
        }
        temp = temp->next;
    }
    //成功找到，则进行更改操作
    if (find == 1) {
        temp->data = newElem;
        return;
    }
    //查找失败，输出提示信息
    printf("链表中未找到目标元素，更改失败\n");
}
//释放链表中结点占用的内存空间
void free_line(Line* head) {
    Line* temp = head;
    while (temp) {
        head = head->next;
        free(temp);
        temp = head;
    }
}

int main()
{
    //创建一个头指针
    Line* head = NULL;
    //调用链表创建函数
    head = initLine(head);
    printf("创建好的双向链表为:\n");
    display(head);

    printf("删除元素 2:\n");
    head = delLine(head, 2);
    display(head);

    printf("元素 3 的位置是：%d\n", selectElem(head, 3));
  
    printf("表中的元素 3 改为 6:\n");
    amendElem(head, 3, 6);
    display(head);

    free_line(head);
    return 0;
}

程序执行结果为：

创建好的双向链表为:
1 <-> 2 <-> 3 <-> 4 <-> 5
删除元素 2:
1 <-> 3 <-> 4 <-> 5
元素 3 的位置是：2
表中的元素 3 改为 6:
1 <-> 6 <-> 4 <-> 5