05贪心算法练习题解析

贪心算法练习题及参考代码

01装满杯子需要的最短总时长

问题描述

现有一台饮水机，可以制备冷水、温水和热水。每秒钟，可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。

给你一个下标从 0 开始、长度为 3 的整数数组 amount ，其中 amount[0]、amount[1] 和 amount[2] 分别表示需要装满冷水、温水和热水的杯子数量。返回装满所有杯子所需的 最少 秒数。

• amount.length == 3
• 0 <= amount[i] <= 100

输入描述

第一行输入三个整数表示 amount 数组

输出描述

输出一个整数代表装满所有杯子所需的最少秒数

输入样例

1 4 2

输出样例

4

参考代码

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int main(){
	vector<int> amount(3);
	cin>>amount[0]>>amount[1]>>amount[2];
	
	sort(amount.begin(), amount.end());
    if (amount[0] + amount[1] <= amount[2]) cout<<amount[2];
    else {
        int t = amount[0] + amount[1] - amount[2];
        cout<<(t + 1) / 2 + amount[2];
    }

    return 0;
} 

02无重叠区间

问题描述

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

• 1 <= intervals.length <= 10^5
• intervals[i].length == 2
• -5 * 10^4 <= starti < endi <= 5 * 10^4

输入描述

第一行输入一个整数n表示区间的个数

之后 n 行，每行两个整数表示区间的开始与结束

输出描述

输出一个整数代表需要移除区间的最小数量

输入样例

4

1 2

2 3

3 4

1 3

输出样例

1

参考代码

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int main(){
	int n;
	cin>>n;
	vector<vector<int>> intervals(n,vector<int>(2));
	for(int i=0;i<n;i++){
		cin>>intervals[i][0]>>intervals[i][1];
	}
	
	sort(intervals.begin(), intervals.end(), [](vector<int> u, vector<int> v) {
            return u[1] < v[1];
        });

    int right = intervals[0][1];
    int ans = 1;
    for (int i = 1; i < n; ++i) {
        if (intervals[i][0] >= right) {
            ++ans;
            right = intervals[i][1];
        }
    }
    cout<<n - ans;
    return 0;
}

03石子游戏

问题描述

Alice 和 Bob 轮流玩一个游戏，Alice 先手。

一堆石子里总共有 n 个石子，轮到某个玩家时，他可以 移出 一个石子并得到这个石子的价值。Alice 和 Bob 对石子价值有 不一样的的评判标准 。双方都知道对方的评判标准。

给你两个长度为 n 的整数数组 aliceValues 和 bobValues 。aliceValues[i] 和 bobValues[i] 分别表示 Alice 和 Bob 认为第 i 个石子的价值。

所有石子都被取完后，得分较高的人为胜者。如果两个玩家得分相同，那么为平局。两位玩家都会采用 最优策略 进行游戏。

请你推断游戏的结果，用如下的方式表示：

• 如果 Alice 赢，返回 1 。

• 如果 Bob 赢，返回 -1 。

• 如果游戏平局，返回 0 。

• n == aliceValues.length == bobValues.length

• 1 <= n <= 10^5

• 1 <= aliceValues[i], bobValues[i] <= 100

输入描述

第一行输入一个整数n表示石头的个数

第二行 n 个由空格分割的整数，代表 aliceValues

第三行 n 个由空格分割的整数，代表 bobValues

输出描述

• 如果 Alice 赢，输出 1 。
• 如果 Bob 赢，输出 -1 。
• 如果游戏平局，输出 0 。

输入样例

2

1 3

2 1

输出样例

1

参考代码

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int main(){
	int n;
	cin>>n;
	vector<int> aliceValues(n);
	vector<int> bobValues(n);
	for(int i=0;i<n;i++){
		cin>>aliceValues[i];
	}
	for(int i=0;i<n;i++){
		cin>>bobValues[i];
	}
	
	vector<vector<int>> mp;
	for(int i = 0; i < n; i++){
			int dis = aliceValues[i] + bobValues[i];
			mp.push_back({dis,i});
		}
	sort(mp.begin(), mp.end(), [](vector<int> u, vector<int> v) {
            return u[1] > v[1];
        }); 
	int sum1 = 0, sum2 = 0;
	for(int i = 0; i < n; i++){
		if(i % 2 == 0) sum1 += aliceValues[mp[i][1]];
		else sum2 += bobValues[mp[i][1]];  
	}
	
	if(sum1 == sum2) cout<<0; 
	else if(sum1 > sum2) cout<<1;
	else cout<<-1;

    return 0;
} 

证明：
假设只有两个石头,对于 a， b 的价值分别是 a1, a2, b1, b2

第一种方案是A取第一个，B取第二个，A与B的价值差是 c1 = a1 - b2
第二种方案是A取第二个，B取第一个，A与B的价值差是 c2 = a2 - b1
那么这两种方案对于A来说哪一种更优，就取决于两个方案的价值差的比较

记 c = c1 - c2 = （a1 - b2） - (a2 - b1) = (a1 + b1) - (a2 + b2)

如果c > 0 那么方案一更优，如果c == 0，那么两种方案价值一样，如果c < 0那么方案二更优

那么比较两个方案的优劣 == 比较 a1 + b1 与 a2 + b2 的优劣 ，
归纳一下就是比较每个下标 i 的 a[i] + b[i] 的优劣

所以贪心的策略：将两组石头的价值合并，每次取价值最大的那一组。

04使括号有效的最少添加

问题描述

只有满足下面几点之一，括号字符串才是有效的：

• 它是一个空字符串，或者

• 它可以被写成 AB （A 与 B 连接）, 其中 A 和 B 都是有效字符串，或者

• 它可以被写作 (A)，其中 A 是有效字符串。

给定一个括号字符串 s ，在每一次操作中，你都可以在字符串的任何位置插入一个括号

• 例如，如果 s = "()))" ，你可以插入一个开始括号为 "(()))" 或结束括号为 "())))" 。

返回 为使结果字符串 s 有效而必须添加的最少括号数。

• 1 <= s.length <= 1000
• s 只包含 '(' 和 ')' 字符。

输入描述

输入一个字符串s

输出描述

输出一个整数表示结果

输入样例

())

输出样例

1

参考代码

#include<iostream>
#include<string>

using namespace std;

int main(){
	string s;
	cin>>s;
	
	int ans = 0;
    int leftCount = 0;
    for (auto &c : s) {
        if (c == '(') {
            leftCount++;
        } else {
            if (leftCount > 0) {
                leftCount--;
            } else {
                ans++;
            }
        }
    }
    ans += leftCount;
	cout<<ans;
    return 0;
} 

05翻转矩阵后的得分

问题描述

给你一个大小为 m x n 的二元矩阵 grid ，矩阵中每个元素的值为 0 或 1 。

一次 移动 是指选择任一行或列，并转换该行或列中的每一个值：将所有 0 都更改为 1，将所有 1 都更改为 0。

在做出任意次数的移动后，将该矩阵的每一行都按照二进制数来解释，矩阵的 得分 就是这些数字的总和。

在执行任意次 移动 后（含 0 次），返回可能的最高分数。

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 20
• grid[i][j] 为 0 或 1

输入描述

第一行输入两个正整数m、n 分别代表矩阵的行数和列数

之后 m 行，每行 n 个用空格分隔的数，代表矩阵内容（只包含 0 和 1 ）

输出描述

输出一个整数表示最高的分数

输入样例

3 4

0 0 1 1

1 0 1 0

1 1 0 0

输出样例

39

参考代码

#include<iostream>
#include<vector>

using namespace std;

int main(){
	int m, n;
	cin>>m>>n;
	vector<vector<int>> grid(m,vector<int>(n));
	for(int i=0;i<m;i++){
		for(int j=0;j<n;j++){
			cin>>grid[i][j];
		}
	}
	
	int ret = m * (1 << (n - 1));
    for (int j = 1; j < n; j++) {
        int nOnes = 0;
        for (int i = 0; i < m; i++) {
            if (grid[i][0] == 1) {
                nOnes += grid[i][j];
            } else {
                nOnes += (1 - grid[i][j]);
            }
        }
        int k = max(nOnes, m - nOnes);
        ret += k * (1 << (n - j - 1));
    }

	cout<<ret;
    return 0;
}

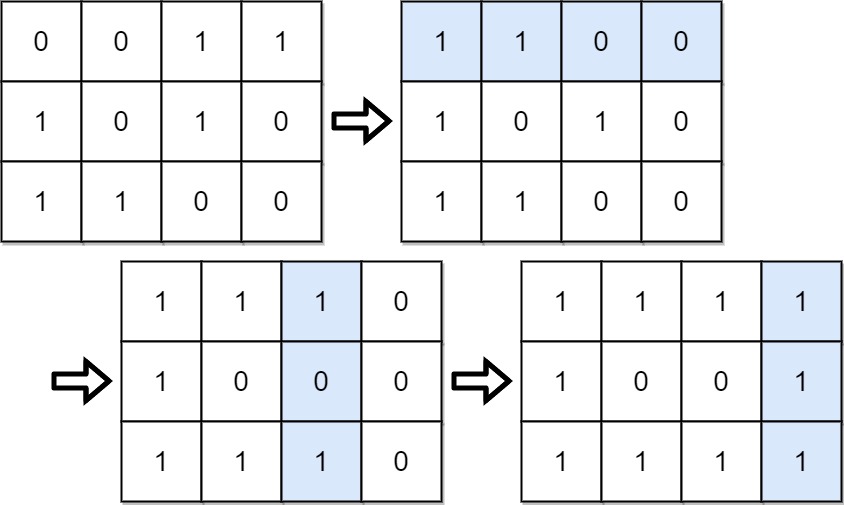
根据题意，能够知道一个重要的事实：给定一个翻转方案，则它们之间任意交换顺序后，得到的结果保持不变。因此，我们总可以先考虑所有的行翻转，再考虑所有的列翻转。

不难发现一点：为了得到最高的分数，矩阵的每一行的最左边的数都必须为 1。为了做到这一点，我们可以翻转那些最左边的数不为 1 的那些行，而其他的行则保持不动。

当将每一行的最左边的数都变为 1 之后，就只能进行列翻转了。为了使得总得分最大，我们要让每个列中1的数目尽可能多。因此，我们扫描除了最左边的列以外的每一列，如果该列 0 的数目多于 1 的数目，就翻转该列，其他的列则保持不变。

实际编写代码时，我们无需修改原矩阵，而是可以计算每一列对总分数的「贡献」，从而直接计算出最高的分数。假设矩阵共有 m 行 n 列，计算方法如下：

• 对于最左边的列而言，由于最优情况下，它们的取值都为 1，因此每个元素对分数的贡献都为 $2^{n-1}$ ，总贡献为 $m\times 2^{n-1}$。

• 对于第 j 列（$j>0$，此处规定最左边的列是第 0 列）而言，我们统计这一列 $0,1$ 的数量，令其中的最大值为 k，则 k 是列翻转后的 1 的数量，该列的总贡献为 $k\times 2^{n-j-1}$ 。需要注意的是，在统计 0,1的数量的时候，要考虑最初进行的行反转。

06柠檬水找零

问题描述

在柠檬水摊上，每一杯柠檬水的售价为 5 元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 元、10 元或 20 元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

• 1 <= bills.length <= 10^5
• bills[i] 不是 5 就是 10 或是 20

输入描述

第一行输入一个正整数n 代表顾客的数量

第二行 n 个用空格分隔的数，代表顾客支付的钱（只包含 5 、10 和 20 ）

输出描述

如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

输入样例

5

5 5 5 10 20

输出样例

true

参考代码

#include<iostream>
#include<vector>

using namespace std;

int main(){
	int n;
	cin>>n;
	vector<int> bills(n);
	for(int i=0;i<n;i++){
		cin>>bills[i];
	}
	
	int five = 0, ten = 0;
    for (auto& bill: bills) {
        if (bill == 5) {
            five++;
        } else if (bill == 10) {
            if (five == 0) {
                cout<<"false";
                return 0;
            }
            five--;
            ten++;
        } else {
            if (five > 0 && ten > 0) {
                five--;
                ten--;
            } else if (five >= 3) {
                five -= 3;
            } else {
            	cout<<"false";
                return 0;
            }
        }
    }
	cout<<"true";
    return 0;
} 

07用最少数量的箭引爆气球

问题描述

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中 points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend 之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

• 1 <= points.length <= 10^5
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

输入描述

第一行输入一个正整数n 代表气球的数量

之后 n 行，每行2个用空格分隔的数，代表气球的 xstart 和 xend

输出描述

输出一个整数，代表引爆所有气球所必须射出的最小弓箭数 。

输入样例

4

10 16

2 8

1 6

7 12

输出样例

2

参考代码

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int main(){
	int n;
	cin>>n;
	vector<vector<int>> points(n,vector<int>(2));
	for(int i=0;i<n;i++){
		cin>>points[i][0]>>points[i][1];
	}
	
	sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v) {
        return u[1] < v[1];
    });
    int pos = points[0][1];
    int ans = 1;
    for (const vector<int>& balloon: points) {
        if (balloon[0] > pos) {
            pos = balloon[1];
            ++ans;
        }
    }
    cout<<ans;

    return 0;
}