大数定律定义:
设随机变量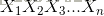
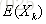
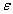
理解:随着样本数量n的增加,样本的平均数(总体中的一部分)将接近于总体样本的平均数,所以在统计推断中一般使用样本平均数估计总体平均数的值。
下面我们用简单的python代码来客观展现出大数定理:
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
# 防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
# 定义数据量大小
numberSize = 200
# 生成服从正态分布的随机数据,其均值为0
randData = np.random.normal(scale=100, size=numberSize)
# 保存随机每增加一个数据后算出来的均值
randData_average = []
# 保存每增加一个数据后的数据和
randData_sum = 0
# 通过循环计算每增加一个数据后的均值
for index in range(len(randData)):
randData_average.append((randData[index] + randData_sum) / (index + 1.0))
# 定义作图的x值和y值
x = np.arange(0,numberSize,1)
y = randData_average
# 作图设置
plt.title('大数定律')
plt.xlabel('数据量')
plt.ylabel('平均值')
# 作图并展示
plt.plot(x,y)
plt.plot([0,numberSize], [0,0], 'r')
plt.show()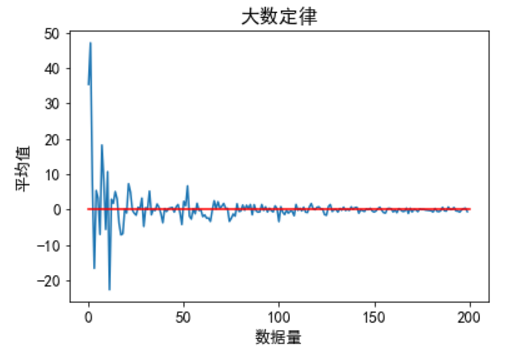
由上图即可进一步验证我们的结论,随着数据量的增加,均值越来越接近实际均值0。
即当我们的样本数据量足够大的时候,我们就可以用样本的平均值来估计总体平均值。








 本文通过Python代码演示了大数定律的基本概念,该定律表明,随着样本数量的增加,样本平均值趋于稳定并接近总体平均值,从而为统计推断提供了依据。
本文通过Python代码演示了大数定律的基本概念,该定律表明,随着样本数量的增加,样本平均值趋于稳定并接近总体平均值,从而为统计推断提供了依据。
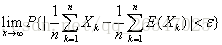
















 2569
2569

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








