堆&&堆排序&&N个数中找出K个最大值&&优先级队列

学习二叉树后，有一个东西需要我们来关注下，就是堆，对于堆，来说我们可以把堆看作一颗完全二叉树。这里我们也可以叫做二叉堆。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

另外，需要关注的就是有一个大堆和一个小堆。
大堆就是父节点的数值大于任何一个子节点的数值。
小堆就是父节点的数值小于任何一个子节点的数值。

1.堆

---

接下来，我们进行堆的创建：
首先我们要清楚，堆的储存结构，在这里作为一颗完全二叉树，我们可以使用数组来存储堆，然后调整数组的下标，这样就可以抽象出一颗完全二叉树。
我们接下来使用STL中的vector来代替数组。

然后这里我们需要它们父节点和子节点的关系：
父节点=（子节点-1）*2；
子节点=父节点*2+1；

1.1堆的创建

---

这样我们就可以根据上述的关系实现找到某个节点的父亲节点或者孩子节点。

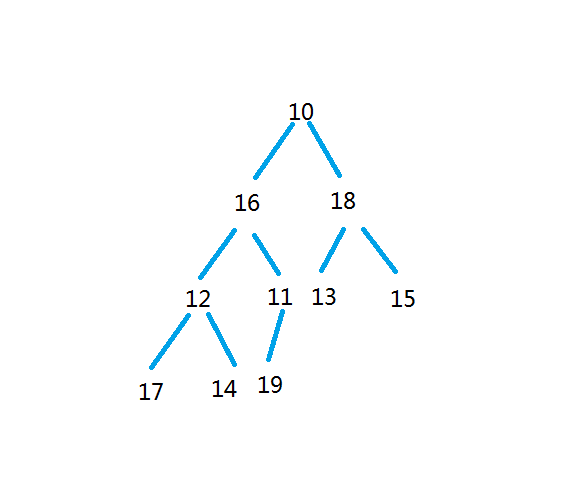
比如，我们给出一个数组：

int a[] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19 };

那么我们就相当于创建了这样的一颗完全二叉树

这就是这颗完全二叉树的关系。

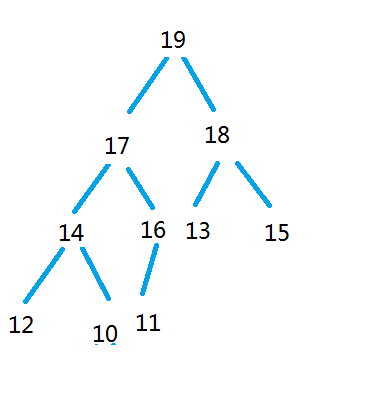
接下来我们需要进行建堆。所谓建堆，其实就是我们所说的进行这颗完全二叉树的调整，根据我们想要大堆还是小堆，进行调整。

调整的方法是，从第倒数第一个非叶子节点进行调整，与它的两个叶子节点进行比较，调整。这个就是堆中的所谓的向下调整法。在这里要注意调整的时候要取出叶子节点中的最值节点（即最小值或者最大值）。然后和父节点进行比较。

void _AdjustDown(int root)
    {
        assert(!_a.empty());
        size_t parent = root;
        size_t child = parent * 2 + 1;
        while (parent<_a.size())
        {
            Compare com;

            if (child + 1<_a.size()
                && com(_a[child + 1], _a[child]))
                //在这里对两个子节点进行判断。看应该取出哪一个
            {
                ++child;
            }
            if (child<_a.size() && com(_a[child], _a[parent]))
            //进行子节点和父节点之间的判断调整
            {
                std::swap(_a[child], _a[parent]);
                parent = child;//调整完后的原父节点依然要和下面的节点进行继续调整。
                child = parent * 2 + 1;
            }
            else
            {
                break;
            }
        }
    }

这就是重要的向下调整法，为了方便对于大小堆的操控，我们引入仿函数，通过仿函数返回值，控制比较的条件。

template<typename T>
//当需要小堆时：
class Less
{
public:
    bool operator ()(const T& a, const T& b)
    {
        return a < b;
    }
};

template<typename T>
//当需要大堆时
class Greater
{
public:
    bool operator ()(const T& a, const T& b)
    {
        return a > b;
    }
};

通过仿函数，我们只需要传入一个模板参数，然后通过创建的对象就可以实现控制是大堆还是小堆。

当我们每次对整个堆进行增加以后，我们都可以采用向下调整法，进行调整，这样就可以调整出新的满足要求的堆。

建堆的时间复杂度：O（N*logN）

1.2堆的插入

---

所以，堆的插入算法也就简单的实现了。
因为我们这里使用的是vector，所以我们直接使用vect