搜索二叉树

最新推荐文章于 2024-09-22 16:37:34 发布
最新推荐文章于 2024-09-22 16:37:34 发布
阅读量1.8k 收藏 2
点赞数 1
分类专栏： 数据结构 一起学习C/C++ 文章标签： 二叉树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_26768741/article/details/52886600
版权

二叉搜索树：它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

二叉搜索树有个特点，最左的是最小的节点，最右的是最大的节点。
当我们把二叉搜索树进行中序遍历的时候，它是进行排序后的结果，所以我们也把二叉搜索树叫做排序二叉树。

接下来我们介绍二叉排序树的所有的算法：

1.1搜索二叉树的结构

首先我们来看它的结构，他的结构和二叉树类似，所以会有一个左孩子节点的指针，一个右孩子节点的指针，还有一个被叫做键值的东西，我们通常来采用这个构建搜索二叉树，然后还有一个叫做关键值，我们用它来保存数据。

template<typename K,typename V>
struct SearchBinaryTreeNode
{
    typedef SearchBinaryTreeNode<K,V> Node;

    SearchBinaryTreeNode(const K& key)
        : _left(NULL)
        , _right(NULL)
        , _key(key)

    {
    }


    V _value;
    Node* _left;
    Node* _right;
    K _key;

};

1.2构建搜索二叉树

构建搜索二叉树，我们这里采用的方式是采用数组来进行构建的。

SearchBinaryTree(const K* arr, size_t size)
    {
        assert(arr);
        for (size_t i = 0; i < size; i++)
        {
            InsertP(arr[i]);
        }

    }

把数组中的每一个元素作为节点，进行插入。

1.3搜索二叉树的插入

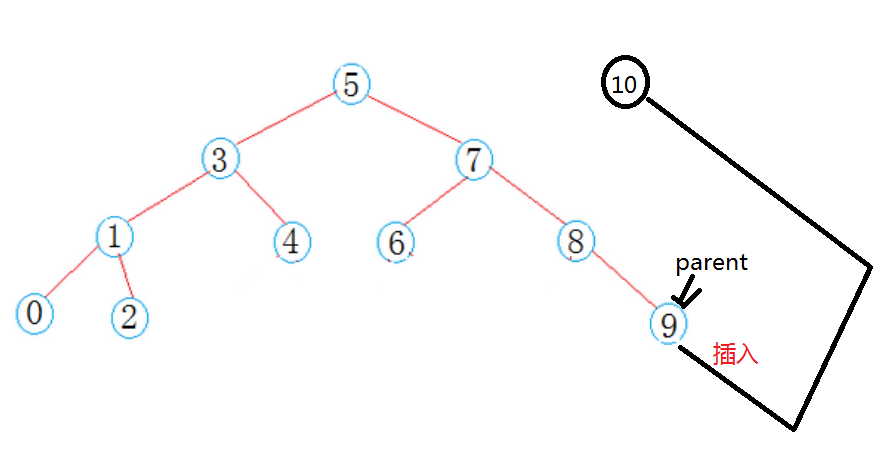
搜索二叉树关键的算法之一，在这里，我们的思路就是当你插入一个节点，必须是所指向的位置为空时才可以查入，所以我们来查找我们所需要插入的位置，如果为空树，那么可以直接进行插入。
其他的用根节点的键值和key进行比较，如果key大于根节点键值，就说明在右子树如果小，那么就说明在右子树，如果相等，就说明已经出现了，不需要再次进行插入。最后如果我们所找到的位置为空那么这个时候我们就可以进行插入，插入的时候要看与父亲节点的key进行比较，如果小插入右边，如果大，插入左边。

这里写图片描述

    bool Insert(const K& key)
    {
        if (_root == NULL)
        {
            _root = new Node(key);
            return true;
        }
        Node *cur = _root;
        Node *parent = _root;
        while (cur)
        {
            if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (curcur->_key>key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }
        Node *tmp = new Node(key);
        if (key > parent->_key)
        {

            parent->_right = tmp;
        }
        else
        {
            parent->_left = tmp;
        }
        return true;
    }

上面完成的是非递归的插入，另外，我们实现递归的插入，思路是一样的。

递归的插入在最后只有找到为空的时候才能进行插入节点，否则就进行递归。

    bool _InsertP(Node *&root, const K& key)
    {
        if (root == NULL)
        {
            root = new Node(key);
            return true;
        }
        if (root->_key > key)
        {
            _InsertP(root->_left, key);
        }
        else if (root->_key < key)
        {
            _InsertP(root->_right, key);
        }
        else
        {
            return false;
        }
        return true;
    }

1.4搜索二叉树的删除

搜索二叉树的删除算法算是最难的了。在这里我们需要考虑几种思路。

  • 没有这个节点
  • 删除根节点
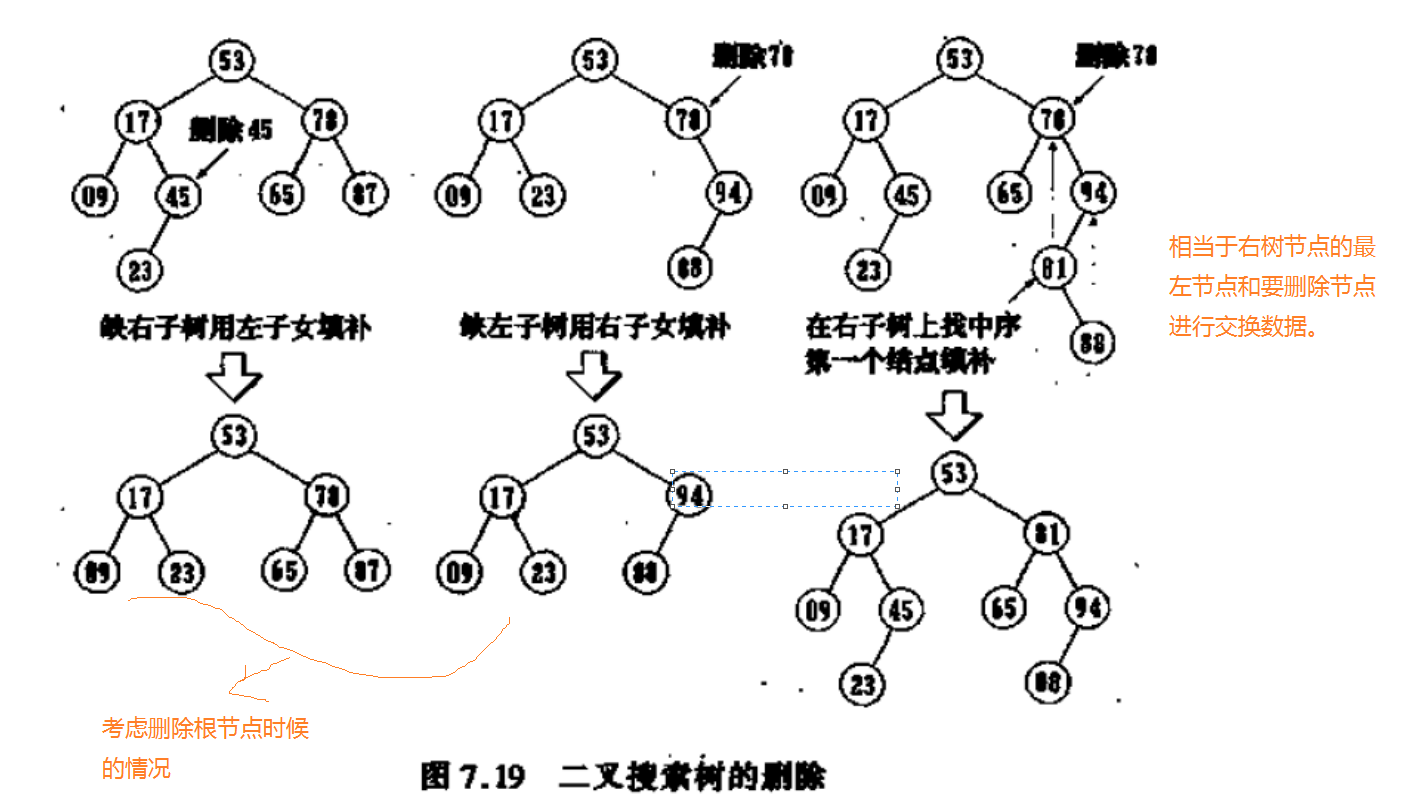
  • 删除左子树为空的节点
  • 删除右子树为空的节点
  • 删除左右子书都不为空的节点

这里写图片描述
首先我们要做的是找到这个节点，然后找到这个节点的算法就类似与查找节点。
接下来我们要做的是分情况进行讨论。

如果没有这个节点，我们就不删了，return。

接下来看它的孩子，当它孩子任意一个为空的时候，看他的孩子时要考虑删除根节点的情况。删除根节点，这个时候终点是改变root，另外的删除其他节点，找到这个节点，然后看这个节点和父亲节点的关系，进行调整就好了。

然后，进行讨论两个孩子都有的情况，首先我们就是利用交换的方式进行删除，思路就是找到删除节点的第一个右子树节点的最左节点或者左子树第一个节点的最右节点。简单的说，就是把根变作左子树最大的或者右子树最小的。

综合这个思路我们就可以完成删除。

    bool Remove(const K& key)
    {
        Node *cur = _root;
        Node *parent = NULL;
        Node *del = NULL;
        while (cur&&cur->_key!=key)
        {
            if (cur->_key < key)
            {

                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_key>key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                break;
            }
        }
        if (cur == NULL)
        {
            return false;   
        }
        if (cur->left == NULL)
        {

            del = cur;
            if (parent == NULL)
            {
                _root = cur->_right;
            }
            else
            {

                if (parent->_left == cur)
                {
                    parent->_left = cur->_right;
                }
                else
                {
                    parent->_right = cur->_right;
                }
            }
        }
        else if (cur->_right==NULL)
        {
            del = cur;
            if (parent == NULL)
            {
                cur = cur->_left;
            }
            else
            {
                if (parent->_left == cur)
                {
                    parent->_left = cur->_left;
                }
                else
                {
                    parent->_right = cur->_right;
                }
            }

        }
        else
        {
            Node *swapnode = cur->_right;
            while (swapnode->_left)
            {
                parent = swapnode;
                swapnode = swapnode->_left;
            }
            del = swapnode;
            cur->_key = swapnode->_key;
            cur->_value = swapnode->_value;

            if (parent->_left == swapnode)
                parent->_left = swapnode->_right;
            else
                parent->_right = swapnode->_right;
        }
        delete del;
        del = NULL;
        return true;
    }

接下来介绍递归的删除：
递归的删除的思路和上面的是一样的，重点是在于理解递归。

递归的时候进行的也先是查找，如果找不到返回，找到进行删除。

这个时候我们也是一样，看root节点的孩子进行分布操作，如果左为空，那么就给root右，右为空，就给左，在这里，其实这个root的含义相当于是parent的左指针或右指针。因为是递归，所以就是上一层函数左指针或者右指针。然后其他的和上面的思路是一样的。

    bool _RemoveP(Node *&root, const K& key)
    {
        if (root == NULL)
        {
            return false;
        }
        if (root->_key < key)
        {
            _RemoveP(root->_right,key);
        }
        else if (root->_key > key)
        {
            _RemoveP(root->_left,key);
        }
        else
        {
            Node* del = root;


            if (root->_left == NULL)
            {
                root = root->_right;
            }
            else if (root->_right == NULL)
            {
                root = root->_left;
            }
            else
            {

                Node* parent = root;
                Node *swapnode = root->_right;
                while (swapnode->_left)
                {
                    parent = swapnode;
                    swapnode = swapnode->_left;
                }
                root->_key = swapnode->_key;
                root->_value = swapnode->_value;
                if (parent->_right == swapnode)
                    parent->_right = swapnode->_right;
                else
                    parent->_left = swapnode->_right;
                del = swapnode;
            }
            delete del;
            return true;
        }
        return false;
    }

1.5搜索二叉树的查找

搜索二叉树的查找，这个算法其实上面我们在删除已经进行过了，下面进行简单的介绍一下，你要搜索的，那么就是和根的key比较，如果大于根的key，那么就找右树，如果小于根的key，那么就找左树。相等，就代表找到了。

bool Find(const K &key)
    {
        if (_root == NULL)
            return false;
        Node *cur = _root;
        while (cur)
        {
            if (key > cur->_key)
            {
                cur = cur->_left;
            }
            else if (key < cur->_key)
            {
                cur = cur->_right;
            }
            else
            {
                return true;
            }
        }
        return false;
    }

下来是递归查找，思路上同，就不多说了。

bool _FindP(Node * root,const K& key)
    {
        if (root == NULL)
        {
            return false;
        }
        if (key < root->_key)
        {
            return _FindP(root->_left, key);
        }
        else if (key>root->_key)
        {
            return _FindP(root->_right, key);
        }
        else
        {
            return true;
        }
        return false;
    }

1.5搜索二叉树的MAX和MIN

另外的算法就是找最小和最大
这两个算法就是查找算法的变形，一个是右子树的最右节点，一个是左子树的最左节点。

    const K& Minvalue()
    {
        assert(_root);
        Node* cur = _root;
        while (cur->_left)
        {
            cur = cur->_left;
        }
        return cur->_value;
    }
    const K& Maxvalue()
    {
        assert(_root);
        Node *cur = _root;
        while (cur->_right)
        {
            cur = cur->_right;
        }
        return cur->_value;
    }

其他搜索二叉树的算法和二叉树的类似，可以查看我的二叉树的博客来查看。
代码（全）：

#pragma once

#include<iostream>
#include<cstdlib>
#include<cassert>
using namespace std;

template<typename K,typename V>
struct SearchBinaryTreeNode
{
    typedef SearchBinaryTreeNode<K,V> Node;

    SearchBinaryTreeNode(const K& key)
        : _left(NULL)
        , _right(NULL)
        , _key(key)

    {
    }


    V _value;
    Node* _left;
    Node* _right;
    K _key;

};

template<typename K,typename V>
class SearchBinaryTree
{
protected:
    typedef SearchBinaryTreeNode<K,V>  Node;

public:
    SearchBinaryTree(const K* arr, size_t size)
    {
        assert(arr);
        for (size_t i = 0; i < size; i++)
        {
            InsertP(arr[i]);
        }

    }
    ~SearchBinaryTree()
    {
        _root=_DestorySBT(_root);

    }
    bool InsertP(const K& key)
    {
        return _InsertP(_root, key);
    }
    bool Insert(const K& key)
    {
        if (_root == NULL)
        {
            _root = new Node(key);
            return true;
        }
        Node *cur = _root;
        Node *parent = _root;
        while (cur)
        {
            if (cur->_key < key)
            {
                parent = cur;
                cur = cur->_right;
            }
            else if (curcur->_key>key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }
        Node *tmp = new Node(key);
        if (key > parent->_key)
        {

            parent->_right = tmp;
        }
        else
        {
            parent->_left = tmp;
        }
        return true;
    }
    bool RemoveP(const K& key)
    {
        return _RemoveP(_root, key);
    }
    bool Remove(const K& key)
    {
        Node *cur = _root;
        Node *parent = NULL;
        Node *del = NULL;
        while (cur&&cur->_key!=key)
        {
            if (cur->_key < key)
            {

                parent = cur;
                cur = cur->_right;
            }
            else if (cur->_key>key)
            {
                parent = cur;
                cur = cur->_left;
            }
            else
            {
                break;
            }
        }
        if (cur == NULL)
        {
            return false;   
        }
        if (cur->left == NULL)
        {

            del = cur;
            if (parent == NULL)
            {
                _root = cur->_right;
            }
            else
            {

                if (parent->_left == cur)
                {
                    parent->_left = cur->_right;
                }
                else
                {
                    parent->_right = cur->_right;
                }
            }
        }
        else if (cur->_right==NULL)
        {
            del = cur;
            if (parent == NULL)
            {
                cur = cur->_left;
            }
            else
            {
                if (parent->_left == cur)
                {
                    parent->_left = cur->_left;
                }
                else
                {
                    parent->_right = cur->_right;
                }
            }

        }
        else
        {
            Node *swapnode = cur->_right;
            while (swapnode->_left)
            {
                parent = swapnode;
                swapnode = swapnode->_left;
            }
            del = swapnode;
            cur->_key = swapnode->_key;
            cur->_value = swapnode->_value;

            if (parent->_left == swapnode)
                parent->_left = swapnode->_right;
            else
                parent->_right = swapnode->_right;
        }
        delete del;
        del = NULL;
        return true;
    }
    void Inorderprint()
    {
        _Inorderprint(_root);
        cout << endl;
    }
    bool Empty()
    {
        return _root == NULL;
    }
    bool Find(const K &key)
    {
        if (_root == NULL)
            return false;
        Node *cur = _root;
        while (cur)
        {
            if (key > cur->_key)
            {
                cur = cur->_left;
            }
            else if (key < cur->_key)
            {
                cur = cur->_right;
            }
            else
            {
                return true;
            }
        }
        return false;
    }
    bool FindP(const K &key)
    {
        return _FindP(_root, key);
    }
    const K& Top()
    {
        return _root->_key;
    }
    const K& Minvalue()
    {
        assert(_root);
        Node* cur = _root;
        while (cur->_left)
        {
            cur = cur->_left;
        }
        return cur->_value;
    }
    const K& Maxvalue()
    {
        assert(_root);
        Node *cur = _root;
        while (cur->_right)
        {
            cur = cur->_right;
        }
        return cur->_value;
    }
protected:
    Node* _DestorySBT(Node *root)
    {
        if (root != NULL)
        {
            root->_left = _DestorySBT(root->_left);
            root->_right = _DestorySBT(root->_right);
            delete root;
            root = NULL;
        }
        return root;
    }
    void _Inorderprint(Node *root)
    {
        if (root == NULL)
            return;
        _Inorderprint(root->_left);
        cout << root->_key << " ";
        _Inorderprint(root->_right);
    }
    bool _InsertP(Node *&root, const K& key)
    {
        if (root == NULL)
        {
            root = new Node(key);
            return true;
        }
        if (root->_key > key)
        {
            _InsertP(root->_left, key);
        }
        else if (root->_key < key)
        {
            _InsertP(root->_right, key);
        }
        else
        {
            return false;
        }
        return true;
    }
    bool _RemoveP(Node *&root, const K& key)
    {
        if (root == NULL)
        {
            return false;
        }
        if (root->_key < key)
        {
            _RemoveP(root->_right,key);
        }
        else if (root->_key > key)
        {
            _RemoveP(root->_left,key);
        }
        else
        {
            Node* del = root;


            if (root->_left == NULL)
            {
                root = root->_right;
            }
            else if (root->_right == NULL)
            {
                root = root->_left;
            }
            else
            {

                Node* parent = root;
                Node *swapnode = root->_right;
                while (swapnode->_left)
                {
                    parent = swapnode;
                    swapnode = swapnode->_left;
                }
                root->_key = swapnode->_key;
                root->_value = swapnode->_value;
                if (parent->_right == swapnode)
                    parent->_right = swapnode->_right;
                else
                    parent->_left = swapnode->_right;
                del = swapnode;
            }
            delete del;
            return true;
        }
        return false;
    }
    bool _FindP(Node * root,const K& key)
    {
        if (root == NULL)
        {
            return false;
        }
        if (key < root->_key)
        {
            return _FindP(root->_left, key);
        }
        else if (key>root->_key)
        {
            return _FindP(root->_right, key);
        }
        else
        {
            return true;
        }
        return false;
    }
protected:
    Node * _root;
};

另外代码已上传github，链接：https://github.com/wsy081414/data-structure/blob/master/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9B%B8%E5%85%B3/%E6%90%9C%E7%B4%A2%E4%BA%8C%E5%8F%89%E6%A0%91.h

【每日一题】调整搜索二叉树中两个错误的节点
junxinsiwo的专栏
11-16 426
一棵二叉树原本是搜索二叉树，但是其中有两个节点调换了位置，使得这棵二叉树不再是搜索二叉树，请找到这两个错误节点并返回。 已知二叉树中所有节点的值都不一样，给定二叉树的头节点 head，返回一个长度为 2 的二叉树节点类型数组 errs，errs[0] 表示一个错误节点，errs[1] 表示另一个错误节点。
二叉树的查找
12-11
创建二叉排序树 的第一种方法（通过insertBST创建） 二叉排序树的查找 （递归实现） * * 查找可以有两种实现方法，一种是递归，一种是while 循环。 * 在插入和删除操作中也首先需要查询操作，这时使用while 循环比较好，可以知道要查询结点的双亲结点
数据结构之搜索二叉树
最新发布
都市隸人的博客
09-22 1079
本文详细介绍了二叉树数据结构的衍生二叉搜索树的模拟实现以及应用
搜索二叉树c语言版本
08-13
搜索二叉树（Binary Search Tree，简称BST）是一种特殊的二叉树数据结构，它具有以下特性：对于树中的任意一个节点，其左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。...
数据结构搜索二叉树.rar
07-16
二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树...
【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归）
02-26
【数据结构】——搜索二叉树的插入，查找和删除（递归&非递归） 在计算机科学中，数据结构是存储和组织数据的方式，它直接影响到数据的处理效率。搜索二叉树（BST，Binary Search Tree）是一种特殊类型的数据结构，...
搜索——搜索二叉树
小白cvnice的博客
10-05 147
搜索二叉树概念： 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值 它的左右子树也分别为二叉搜索树 程序： class Node(): """创建树节点""" def __init__(self,val=None, left = None, rig...
查找二叉树(tree_a)
蔡军帅
04-19 1618
查找二叉树(tree_a) 问题 E: 查找二叉树(tree_a) 时间限制:1 Sec内存限制:128 MB提交:206解决:152[提交][状态][讨论版][命题人:quanxing][Edit] [TestData] [同步数据] 题目描述 已知一棵二叉树用邻接表结构存储，中序查找二叉树中值为x的结点，并指出是第几个结点(通过中序遍历访问的 第几个节点...
查找二叉树（BST）
WHTGS的博客
03-04 265
今天分享一些关于BST的内容： 一、基础知识点 1 一棵树最上面的节点称为根节点，如果一个节点下面连接多个节点，那么该节点称为父节点，，，它下面的节点称为子节点。一个节点可以有0个 1个 或多个子节点，没有任何子节点的节点称为叶子节点 2 以某种特定的顺序访问树中所有的节点称为树的遍历 3 树可以分为几个层次，根节点是第0层，子节点是第1层，子节点的子节点是第2层，依次类推 二、今天的主角...
二叉树搜索
weixin_34122810的博客
07-07 95
删除数值一般来说，须要依据以下几种情况分别进行处理： 1.须要删除的节点没有左儿子，那么把右儿子提上去 2.须要删除的节点的左儿子没有右儿子，那么就把左儿子提上去 3.以上两种情况都不满足的话，就把左儿子的子孙中最大的节点提到须要删除的节点上 和堆一样。非常多情况下不须要自己实现二叉搜索树，使用C++中的STL，STL里有set和map容器， set是使用erc搜索树维护集合的容器，而...
二叉树——搜索二叉树
weixin_68644350的博客
10-23 877
详解二叉搜索树的实现以及时间复杂度和缺陷
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值