语音回声抑制算法

1. 语音降噪原理

1.1 声学回声消除系统

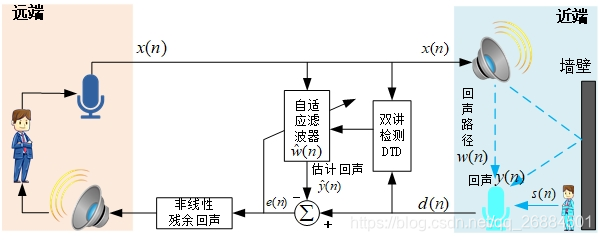
声学回声消除（Acoustic Echo Cancellation，AEC），一个完整的回声消除系统，包含以下几个模块

1. 时延估计（Time Delay Estimation, TDE） 模块
2. (线性)回声消除（Linear Acoustic Echo Cancellation, AEC） 模块
3. 双讲检测（Double-Talk Detect, DTD） 模块
4. 非线性残余声学回声抑制（Residual Acoustic Echo Suppression, RAES） 模块
   

1.2 滤波器有两种状态

1. 滤波：$e(n)=d(n)-\hat{y}(n)$
2. 自适应滤波器系数更新(NLMS)：$\hat{w}(n+1)=\hat{w}(n)+\mu e(n)\frac{x(n)}{x^T(n)x(n)}$

1.3 自适应滤波器

针对自适应滤波器有三种工作模式（通过DTD双讲检测）：

1. 远端语音存在，近端语音不存在：滤波、自适应滤波器系数更新
2. 远端语音存在，近端语音存在：滤波
3. 远端语音不存在：什么都不用做

1.4 回声抑制算法

使用自适应滤波算法调整滤波器的权值向量，估计一个近似的回声路径来逼近真实回声路径，从而得到估计的回声信号，并在纯净语音和回声的混合信号中除去此信号来实现回声的消除。

𝑥(𝑛)为远端语音，经过未知的回声路径𝑤(𝑛)得到远端回声语音𝑦(𝑛)=𝑥(𝑛)∗𝑤(𝑛)，再加上近端语音𝑠(𝑛)，得到期望信号𝑑(𝑛)=𝑦(𝑛)+𝑠(𝑛)。x(n)通过自适应滤波器𝑤̂ (𝑛)得到估计的回声信号𝑦̂ (𝑛)，并与期望信号𝑑(𝑛)相减得到误差信号𝑒(𝑛)=𝑑(𝑛)−𝑦̂ (𝑛)，误差信号的值越小说明自适应滤波算法所估计的回声路径就越接近实际的回声路径。
滤波器采用特定的自适应算法不停地调整权值向量，使估计的回声路径𝑤̂ (𝑛)逐渐趋近于真实回声路径𝑤(𝑛)。显然，在 AEC 问题中，自适应滤波器的选择对回声消除的性能好坏起着十分关键的作用。

2. 自适应滤波算法及代码实现

2.1 LMS算法

2.1.1 原理

通过上面AEC的基本原理我们知道了误差信号𝑒(𝑛)等于期望信号𝑑(𝑛)减去滤波器输出信号𝑦̂ ：
$$e(n)=d(n)-\hat{w}(n)x(n)$$
运用最小均方误差准则，通过对其求导并令其等于0，求使得误差|𝑒(𝑛)|2最小时的𝑤̂ （因为|𝑒(𝑛)|在最小点不可导，所以使用的是|𝑒(𝑛)|2），对于LMS算法，其滤波器系数迭代公式为
$$\begin{array}{rl}w(n+1)& =w(n)-\mu \frac{\partial e(n{)}^2}{\partial w}\\ & =w(n)-2\mu e(n)\frac{\partial (d(n)-\hat{w}\ast x(n))}{\partial w}\\ & =w(n)+2\mu e(n)x(n)\end{array}$$