卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,如果卡方值越大,二者偏差程度越大;反之,二者偏差越小;若两个值完全相等时,卡方值就为0,表明理论值完全符合。
1.适合性检验
卡方适合性检验的目的是为了检查所抽取的样本是符合与预期值。(是否符合理论值)
例:统计一羊场全年所产876只羔羊中,有公羔428只,母羔448只,根据遗传学理论,公母比应为1:1,试分析其是否符合理论。
A为实际观测值,T为理论值,卡方值
可建立下表:
| 性别 | 实际观测次数A | 理论次数T |
| 公 | 428 | 438 |
| 母 | 448 | 438 |
data sheep;
input a b@@;
cards;
1 428 2 448
;
proc freq;
table a/testf=(438 438);
weight b;
run;也可以按概率写为:
data sheep;
input a b@@;
cards;
1 428 2 448
;
proc freq;
table a/testp=(0.5 0.5);
weight b;
run;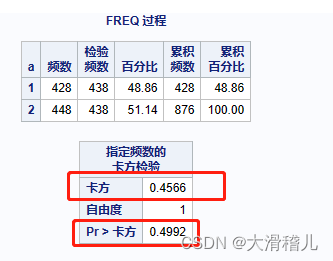
答:卡方值=0.4566,实际观测次数与理论值接近。
2.独立性检验
用于判断两类因子是独立还是彼此相关。与适合性检验相比,独立性检验无现成的理论与学说可利用,理论次数在两因子相互独立的假设下计算,自由度不同。
例:甲乙两地水牛体型按优良中劣四个等级分类,统计结果如下,问两地水牛体型构成是否相同?
| 优 | 良 | 中 | 劣 | |
| 甲 | 10 | 10 | 60 | 10 |
| 乙 | 10 | 5 | 20 | 10 |
Data buffalo;
Do a=1 to 2;
Do b=1 to 4;
Input c@@;
Output;
End;
End;
Cards;
10 10 60 10 10 5 20 10
;
Proc freq;
Table a*b/chisq;
Weight c;
Run;
p>0.05,不能否定无效假设,可以认为两地水牛体型构成比例相同。
尤其注意:独立性检验的样本值的不同,可能会影响卡方值的选取!
当表格R*C为2*2时,还有结果中还会出现连续调整卡方与Fisher 精确检验。
N为样本总数,T为理论频数(期望计数)
1)Pearson卡方(此为默认的卡方):N≥40,且所有T≥5时,使用Pearson卡方获取结果结论
2)连续校正:N≥40,任意一个最小理论频数1≤T<5时,用连续校正卡方检验
3)Fisher精确概率:N≥40,2个及以上最小理论频数1≤T<5时,用Fisher精确概率检验的结果
4)N<40,或存在任意T<1时,用Fisher精确概率检验的结果
5)当卡方检验概率P值接近于α=0.05时,建议用Fisher精确检验
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








