田渊栋：求道之人，不问寒暑（十）

zenRRan

于 2024-10-10 19:47:34 发布

阅读量62

点赞数

原文链接：https://mp.weixin.qq.com/s?__biz=MzI3ODgwODA2MA==&mid=2247532401&idx=1&sn=4fdc85af18b5dfe937e967b3fc55d766&chksm=ea1413680de8ecd389203fee17e1501d77e6e65c76dd7eaca3b51b10c8b4a0fc73a776cd1280&scene=126&sessionid=0

版权

知乎：田渊栋

链接：https://zhuanlan.zhihu.com/p/858144114

好久没写这个系列了，一方面是因为我最近实在比较忙，另一方面也是想要等一等，分享自己觉得挺重要的结果。这次正好在去COLM的飞机上有点空，写一点。

从第一篇田渊栋：求道之人，不问寒暑开始，这个系列已经写了快九年了，与其说它是推广某几篇具体的研究工作，不如说是总结深度学习理论探索之路上的酸甜苦辣。这条路很难走，所以在别人问及的时候，我经常说这个方向是随便玩玩的个人项目，不会帮着公司大张旗鼓地招人，也不是很建议刚读博士的学生去钻研这些，因为一不小心就要掉坑里找不到工作了。

在大模型和Scaling law大行其道的今天，在“海量计算和数据就是王道”的言论日夜轰炸之下，能坚持走下去的人也越来越少，肉眼可见很多理论界的大佬都放弃了。不过对我来说，深度学习这个席卷各个领域，如此有效的框架，没有一个成体系的理论架构是绝对不可想象的。假以时日，这里面肯定有大金矿被挖出来，只是还需要耐心罢了。

如果大家都不搞了，那也许将来人类崭新的道路就会胎死腹中。想到这里，自己出点力也是应该的。

去年我们做了Scan&Snap (NeurIPS'23)及JoMA (ICLR'24)这两个分析Transformer的注意力机制（attention mechanism）的动力学理论框架，对注意力机制为什么会出现稀疏性，及它对网络学习的帮助有了一些深入的理解。总的来说，注意力机制正如其名，是在纷繁复杂的数据中找到相关性（correlation）最强的部分并予以重点学习的机制。数据中会出现很多存在相关性却不强的部分，这些弱相关性因为一些偶然而产生（比如说训练数据中的巧合和随机涨落），并非本质，却会欺骗模型，让它没能学到最重要的关联性。在Scan&Snap这篇文章中，我们聚焦于一层注意力层加线性FFN，证明了注意力（attention）会让让强关联变得更强，而弱关联变得更弱，这样模型能集中火力学习强关联，从而达到更好的泛化能力。

JoMA在这基础了做了扩展，展示了在非线性FFN和多层网络的情况下，注意力机制不仅能学到强关联的数据，只要训练时间够长，也还能逐渐学到弱关联性。只是这个学习过程在训练动力学上是分开的，按照时序先学强关联，这样那些被多层级联的强关联所附带产生的弱关联就不用学了，然后再逐渐学剩下的弱关联性。这样带注意力机制的Transformer就能把两者都学到，而不需要预先告诉模型，数据关联到什么程度才值得重点学。这种自适应数据集结构的能力，是Transformer厉害的地方。

然而Scan&Snap及JoMA这两篇文章的共同局限在于，它们主要建模“数据里的哪些知识被模型学到了”，而并没有深入建模“模型究竟怎么学的，学出来的隐空间向量里面究竟有什么东西”。对于一般数据集，这个问题暂时太难，因此这一次我们聚焦于特定的数学推理问题，它们有已知的良好结构，我们只需要研究网络是否能发现它们，以什么样的形式发现它们，就行了。

这就引出了这一次的工作Composing Global Optimizers to Reasoning Tasks via Algebraic Objects in Neural Nets。

这次我们选定的特定问题是（取模）加法。许多文章已经在实验中发现大模型在做加法的时候，并非简单地记住一张加法表格然后进行检索，而用的是傅立叶表示，通过一些三角函数里的神奇操作来间接地计算两个数的和，一些文章做了许多实验来分析它的一些性质，但因为神经网络的高度非线性，并没有特别好的理论框架去解释它。在这篇文章里，我们运用近世代数的一些基本概念，找到了一个可能的框架。

文章的思路非常直接：首先，我们发现不同大小的两层神经网络的解空间放在一起，满足一个半环的结构；其次，目标函数（MSE Loss）可以展开为一些项的平方和，其中每个项都是从这个半环到复数域上的同态映射。这样的话，如果要找到这个目标函数的全局最优解，那完全可以把每个项单独拿出来，找各自的最优解，然后把这些各自的最优解用半环上的运算（也即是半环上的加法和乘法）拼起来，变成全局最优解。

我们发现损失函数的代数结构和2层神经网络的代数特性有重要的联系，可以利用这个结构来自下而上构造全局最优解。

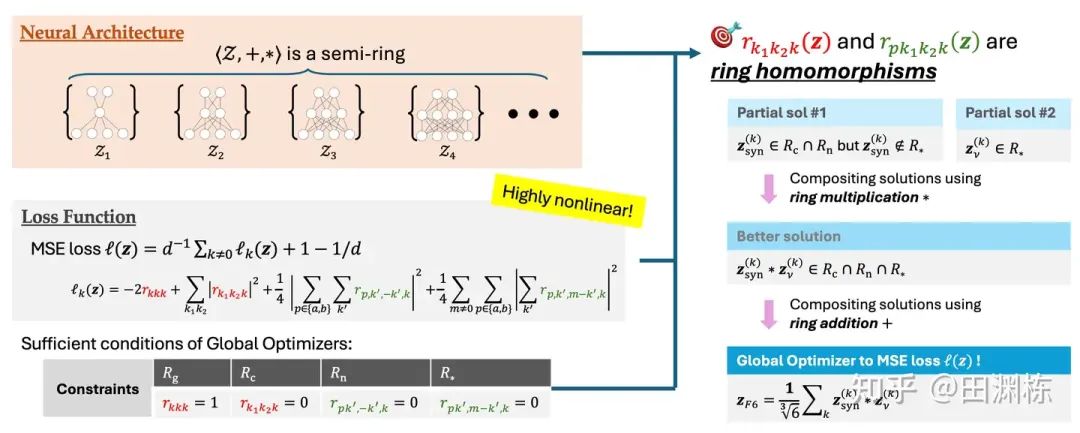
用这种构造方法可以系统性地得到大量全局最优解，也可以证明有无穷个这样的最优解，不仅如此，我们还能证明这些解之间在拓扑上的连通性，利用这种连通性，带正则化的梯度下降，自然会收敛到最为简单的全局最优解。

这样就把“用2层神经网络拟和取模加法”这个任务里的解空间结构，较为完整地刻画下来了。当然构造最优解这本身并不稀奇，大量过往的文章都可以做到这一点，但在构造完了之后，我们进一步发现，这些构造解，和真的用Adam梯度下降跑出来的，完全一致。具体来说，不管中间层的神经元有多少个，过参化的程度如何，在梯度下降收敛时，最终每个频率上存在阶为4的解和阶为6的解（“阶“指的是这个解由多少个神经元共同组成），并且在这些解中，有95%的解还能按照半环的乘法分解成“2x2”和“2x3”的形式，并且每个部分都能对上理论的构造。