问题及代码:
文件名称:main.cpp btree.h btree.cpp
作者:郑孚嘉
问题描述:运行并重复测试教学内容中涉及的算法。改变测试数据进行重复测试的意义在于,可以从更多角度体会算法,以达到逐渐掌握算法的程度。使用你的测试数据,并展示测试结果,观察运行结果,以此来领会算法。
(1)层次遍历算法的验证
(2)二叉树构造算法的验证
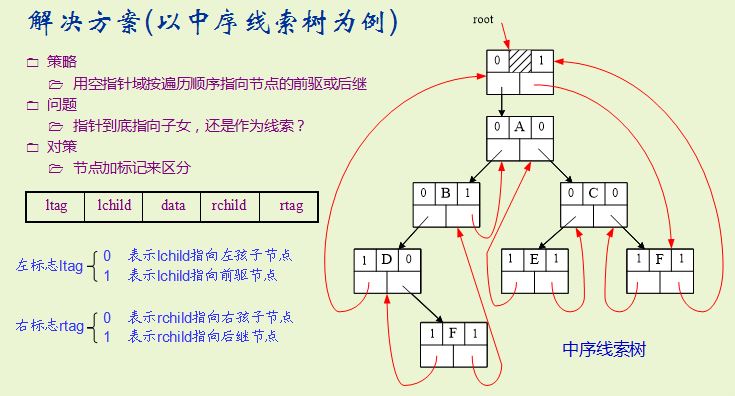
(3)中序线索化二叉树的算法验证
(4)哈夫曼编码的算法验证
代码:
(1)实现二叉树的层次遍历算法,并对用”A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))”创建的二叉树进行测试。
main.cpp
#include <stdio.h>
#include "btree.h"
void LevelOrder(BTNode *b)
{
BTNode *p;
BTNode *qu[MaxSize]; //定义环形队列,存放节点指针
int front,rear; //定义队头和队尾指针
front=rear=-1; //置队列为空队列
rear++;
qu[rear]=b; //根节点指针进入队列
while (front!=rear) //队列不为空
{
front=(front+1)%MaxSize;
p=qu[front]; //队头出队列
printf("%c ",p->data); //访问节点
if (p->lchild!=NULL) //有左孩子时将其进队
{
rear=(rear+1)%MaxSize;
qu[rear]=p->lchild;
}
if (p->rchild!=NULL) //有右孩子时将其进队
{
rear=(rear+1)%MaxSize;
qu[rear]=p->rchild;
}
}
}
int main()
{
BTNode *b;
CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");
printf("二叉树b: ");
DispBTNode(b);
printf("\n");
printf("层次遍历序列:\n");
LevelOrder(b);
DestroyBTNode(b);
return 0;
}
运行结果:
(2)先序和中序构造
main.cpp
#include <stdio.h>
#include <malloc.h>
#include "btree.h"
BTNode *CreateBT1(char *pre,char *in,int n)
/*pre存放先序序列,in存放中序序列,n为二叉树结点个数,
本算法执行后返回构造的二叉链的根结点指针*/
{
BTNode *s;
char *p;
int k;
if (n<=0) return NULL;
s=(BTNode *)malloc(sizeof(BTNode)); //创建二叉树结点*s
s->data=*pre;
for (p=in; p<in+n; p++) //在中序序列中找等于*ppos的位置k
if (*p==*pre) //pre指向根结点
break; //在in中找到后退出循环
k=p-in; //确定根结点在in中的位置
s->lchild=CreateBT1(pre+1,in,k); //递归构造左子树
s->rchild=CreateBT1(pre+k+1,p+1,n-k-1); //递归构造右子树
return s;
}
int main()
{
ElemType pre[]="ABDGCEF",in[]="DGBAECF";
BTNode *b1;
b1=CreateBT1(pre,in,7);
printf("b1:");
DispBTNode(b1);
printf("\n");
return 0;
}
中序和后序构造
#include <stdio.h>
#include <malloc.h>
#include "btree.h"
BTNode *CreateBT2(char *post,char *in,int n)
/*post存放后序序列,in存放中序序列,n为二叉树结点个数,
本算法执行后返回构造的二叉链的根结点指针*/
{
BTNode *s;
char r,*p;
int k;
if (n<=0) return NULL;
r=*(post+n-1); //根结点值
s=(BTNode *)malloc(sizeof(BTNode)); //创建二叉树结点*s
s->data=r;
for (p=in; p<in+n; p++) //在in中查找根结点
if (*p==r)
break;
k=p-in; //k为根结点在in中的下标
s->lchild=CreateBT2(post,in,k); //递归构造左子树
s->rchild=CreateBT2(post+k,p+1,n-k-1); //递归构造右子树
return s;
}
int main()
{
ElemType in[]="DGBAECF",post[]="GDBEFCA";
BTNode *b2;
b2=CreateBT2(post,in,7);
printf("b2:");
DispBTNode(b2);
printf("\n");
return 0;
}运行结果:
(3)main.cpp
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
typedef char ElemType;
typedef struct node
{
ElemType data;
int ltag,rtag; //增加的线索标记
struct node *lchild;
struct node *rchild;
} TBTNode;
void CreateTBTNode(TBTNode * &b,char *str)
{
TBTNode *St[MaxSize],*p=NULL;
int top=-1,k,j=0;
char ch;
b=NULL; //建立的二叉树初始时为空
ch=str[j];
while (ch!='\0') //str未扫描完时循环
{
switch(ch)
{
case '(':
top++;
St[top]=p;
k=1;
break; //为左结点
case ')':
top--;
break;
case ',':
k=2;
break; //为右结点
default:
p=(TBTNode *)malloc(sizeof(TBTNode));
p->data=ch;
p->lchild=p->rchild=NULL;
if (b==NULL) //*p为二叉树的根结点
b=p;
else //已建立二叉树根结点
{
switch(k)
{
case 1:
St[top]->lchild=p;
break;
case 2:
St[top]->rchild=p;
break;
}
}
}
j++;
ch=str[j];
}
}
void DispTBTNode(TBTNode *b)
{
if (b!=NULL)
{
printf("%c",b->data);
if (b->lchild!=NULL || b->rchild!=NULL)
{
printf("(");
DispTBTNode(b->lchild);
if (b->rchild!=NULL) printf(",");
DispTBTNode(b->rchild);
printf(")");
}
}
}
TBTNode *pre; //全局变量
void Thread(TBTNode *&p)
{
if (p!=NULL)
{
Thread(p->lchild); //左子树线索化
if (p->lchild==NULL) //前驱线索
{
p->lchild=pre; //建立当前结点的前驱线索
p->ltag=1;
}
else p->ltag=0;
if (pre->rchild==NULL) //后继线索
{
pre->rchild=p; //建立前驱结点的后继线索
pre->rtag=1;
}
else pre->rtag=0;
pre=p;
Thread(p->rchild); //右子树线索化
}
}
TBTNode *CreaThread(TBTNode *b) //中序线索化二叉树
{
TBTNode *root;
root=(TBTNode *)malloc(sizeof(TBTNode)); //创建根结点
root->ltag=0;
root->rtag=1;
root->rchild=b;
if (b==NULL) //空二叉树
root->lchild=root;
else
{
root->lchild=b;
pre=root; //pre是*p的前驱结点,供加线索用
Thread(b); //中序遍历线索化二叉树
pre->rchild=root; //最后处理,加入指向根结点的线索
pre->rtag=1;
root->rchild=pre; //根结点右线索化
}
return root;
}
void ThInOrder(TBTNode *tb)
{
TBTNode *p=tb->lchild; //指向根结点
while (p!=tb)
{
while (p->ltag==0) p=p->lchild;
printf("%c ",p->data);
while (p->rtag==1 && p->rchild!=tb)
{
p=p->rchild;
printf("%c ",p->data);
}
p=p->rchild;
}
}
int main()
{
TBTNode *b,*tb;
CreateTBTNode(b,"A(B(D(,G)),C(E,F))");
printf(" 二叉树:");
DispTBTNode(b);
printf("\n");
tb=CreaThread(b);
printf(" 线索中序序列:");
ThInOrder(tb);
printf("\n");
return 0;
}
运行结果:
(4)main.cpp
#include <stdio.h>
#include <string.h>
#define N 50 //叶子结点数
#define M 2*N-1 //树中结点总数
//哈夫曼树的节点结构类型
typedef struct
{
char data; //结点值
double weight; //权重
int parent; //双亲结点
int lchild; //左孩子结点
int rchild; //右孩子结点
} HTNode;
//每个节点哈夫曼编码的结构类型
typedef struct
{
char cd[N]; //存放哈夫曼码
int start;
} HCode;
//构造哈夫曼树
void CreateHT(HTNode ht[],int n)
{
int i,k,lnode,rnode;
double min1,min2;
for (i=0; i<2*n-1; i++) //所有结点的相关域置初值-1
ht[i].parent=ht[i].lchild=ht[i].rchild=-1;
for (i=n; i<2*n-1; i++) //构造哈夫曼树
{
min1=min2=32767; //lnode和rnode为最小权重的两个结点位置
lnode=rnode=-1;
for (k=0; k<=i-1; k++)
if (ht[k].parent==-1) //只在尚未构造二叉树的结点中查找
{
if (ht[k].weight<min1)
{
min2=min1;
rnode=lnode;
min1=ht[k].weight;
lnode=k;
}
else if (ht[k].weight<min2)
{
min2=ht[k].weight;
rnode=k;
}
}
ht[i].weight=ht[lnode].weight+ht[rnode].weight;
ht[i].lchild=lnode;
ht[i].rchild=rnode;
ht[lnode].parent=i;
ht[rnode].parent=i;
}
}
//实现哈夫曼编码
void CreateHCode(HTNode ht[],HCode hcd[],int n)
{
int i,f,c;
HCode hc;
for (i=0; i<n; i++) //根据哈夫曼树求哈夫曼编码
{
hc.start=n;
c=i;
f=ht[i].parent;
while (f!=-1) //循序直到树根结点
{
if (ht[f].lchild==c) //处理左孩子结点
hc.cd[hc.start--]='0';
else //处理右孩子结点
hc.cd[hc.start--]='1';
c=f;
f=ht[f].parent;
}
hc.start++; //start指向哈夫曼编码最开始字符
hcd[i]=hc;
}
}
//输出哈夫曼编码
void DispHCode(HTNode ht[],HCode hcd[],int n)
{
int i,k;
double sum=0,m=0;
int j;
printf(" 输出哈夫曼编码:\n"); //输出哈夫曼编码
for (i=0; i<n; i++)
{
j=0;
printf(" %c:\t",ht[i].data);
for (k=hcd[i].start; k<=n; k++)
{
printf("%c",hcd[i].cd[k]);
j++;
}
m+=ht[i].weight;
sum+=ht[i].weight*j;
printf("\n");
}
printf("\n 平均长度=%g\n",1.0*sum/m);
}
int main()
{
int n=8,i; //n表示初始字符串的个数
char str[]= {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h'};
double fnum[]= {0.07,0.19,0.02,0.06,0.32,0.03,0.21,0.1};
HTNode ht[M];
HCode hcd[N];
for (i=0; i<n; i++)
{
ht[i].data=str[i];
ht[i].weight=fnum[i];
}
printf("\n");
CreateHT(ht,n);
CreateHCode(ht,hcd,n);
DispHCode(ht,hcd,n);
printf("\n");
return 0;
}运行结果:
知识点总结:
层次遍历是运用一个环形队列储存节点的信息。
构造二叉树时
1.由先序序列和中序序列构造二叉树
定理:任何n(n≥0)个不同节点的二叉树,都可由它的中序序列和先序序列唯一地确定。
- 证明(数学归纳法)
基础:当n=0时,二叉树为空,结论正确。
假设:设节点数小于n的任何二叉树,都可以由其先序序列和中序序列唯一地确定。 b0b1…bk−1bkbk+1…bn−1
归纳:已知某棵二叉树具有n(n>0)个不同节点,其先序序列是 a0~an-1;中序序列b0~bn-1
- 先序遍历“根-左-右”, a0 必定是二叉树的根节点
-
a0
必然在中序序列中出现,设在中序序列中必有某个bk (0<=k<=n-1)
, a0就是根节点。
- 由于bk是根节点,中序遍历“左-根-右”,故中序序列中 b0~bk-1 必是根节点 bk(a0) 左子树的中序序列,即bk 的左子树有k个节点,bk+1~bn-1 必是根节点 bk(a0) 右子树的中序序列,即bk 的右子树有n-k-1 个节点。
- 对应先序序列,紧跟在根节点
a0
之后的k个节点a1~ak
是左子树的先序序列,ak+1~an-1
这n-k-1
就是右子树的先序序列。
- 根据归纳假设,子先序序列a1~ak 和子中序序列b0~bk-1可以唯一地确定根节点 a0 的左子树,而先序序列ak+1~an-1 和子中序序列 bk+1~bn-1 ,可以唯一地确定根节点 a0 的右子树。
- 综上所述,这棵二叉树的根节点己经确定,而且其左、右子树都唯一地确定了,所以整个二叉树也就唯一地确定了。
-
例
2.由后序序列和中序序列构造二叉树
- 定理:任何n(n>0)个不同节点的二叉树,都可由它的中序序列和后序序列唯一地确定。
中序线索树
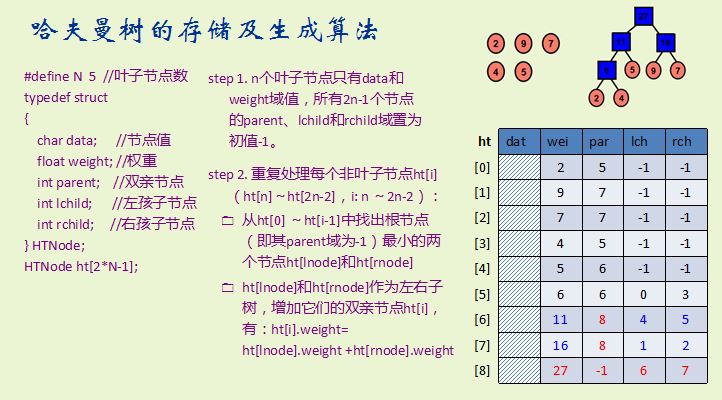
哈夫曼树
运用了寻找最小的两个叶子节点的算法,来构造哈夫曼树。使其路径最短。





























 611
611

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








