LLM-BLENDER: Ensembling Large Language Models with Pairwise Ranking and Generative Fusion翻译

摘要

我们提出了LLM-BLENDER，这是一个结ensemble框架，旨在通过利用多种开源大语言模型（LLM）的多样性优势来实现卓越的性能。我们的框架由两个模块组成：PAIRRANKER和GENFUSER，主要用于解决以下观察结果，即不同样例训练的最优LLM可能会有较大差别。PAIRRANKER采用专门的成对比较方法来区分候选输出之间的细微差异。它共同编码输入文本和一对候选输出，并使用交叉注意力编码器来确定最优输出。我们的结果表明，PAIRRANKER与基于ChatGPT的排名表现出最高的相关性。然后，GENFUSER的目标是合并top-rank的候选输出，通过利用其优势并减轻其弱点来改进输出。为了促进大规模评估，我们介绍了一个基准数据集MixInstruct，这是采用成对比较的多指令混合数据集。我们的LLM-BLENDER在各种指标上的表现明显优于单个LLM和基线方法，并建立了巨大的性能差距。

1.介绍

　　大型语言模型（LLM）在各种任务中表现出令人印象深刻的性能，这主要是由于其指令遵循和访问广泛高质量数据的能力，并在通用人工智能方向展现了有希望的未来。但是，诸如GPT-4和PaLM之类的优秀LLM都是闭源的，这限制了对其网络结构和训练数据的了解。Pythia，LLaMA和Flan-T5等开源LLM提供了在自定义指令数据集中微调这些模型的机会，从而可以开发较小但高效的LLM，例如Alpaca，Vicuna，OpenAssistant和MPT。
　　由于数据，结构和超参数的变化，开源LLM具有多种优势和劣势，使它们彼此互补。图1说明了在我们收集的5,000条指令中最佳LLM的分布。可以在5.1节中找到更多排名细节。尽管Vicuna的百分比最高，但仅在21.22％的样例中是排名第一的。此外，饼图表明，不同样例的最佳LLM可能会大大变化，并且没有一个开源LLM能占据主导。因此，动态ensemble这些LLM，来为每一个输入生成生成更好的响应是非常重要的。考虑到LLM各自的优势和劣势，开发一种ensemble方法来利用其互补潜力，从而提高了鲁棒性，泛化性和准确性，这一点至关重要。通过结合他们独特的贡献，我们可以减轻单个LLM中的偏见，错误和不确定性，从而使输出与人类偏好更好地保持一致。
　　我们介绍了LLM-BLENDER，这是一个ensemble框架，旨在通过混合多个LLM的输出来达到一致的出色性能。LLM-BLENDER包括两个模块：PAIRRANKER和GENFUSER。最初，PAIRRANKER比较了N个LLM的输出，然后GENFUSER融合了最终top-K个排名输出。
　　现有方法，包括InstructGPT中的奖赏模型，用于从给定输入$x$上，对语言模型（LM）的输出进行排名 { y 1 , . . . , y N } \{y_1,...,y_N\} {y1​,...,yN​}，这主要集中于通过编码模块$s_i=f_{\varphi }(x,y_i)$，对基于$x$的每个$y_i$分别评分。尽管当候选输出的差异显而易见时，这个排名目标可能是有效的，但是在结合LLM时，它可能不会那么有效。在LLM的输出候选中，候选差异可能非常微妙，因为它们都是由非常复杂的模型产生的，并且一个可能只比另一个更好。即使对于人类，衡量候选输出的质量而无直接比较也可能具有挑战性。
　　因此，我们提出了一种专门的成对比较方法，PAIRRANKER（第3节），以有效地识别候选输出之间的细微差异并增强排名性能。特别是，我们首先收集每个输入的来自$N$个模型的输出（例如，图1中$N=11$），然后创建其输出的$N(N-1)/2$对。我们以$f_{\varphi }(x,y_i,y_j)$的形式使用共同编码输入$x$以及两个候选者输出$y_i$和$y_j$，来作为交叉注意力编码器的输入（例如RoBERTa），以学习和确定哪个候选更好。
　　在推理阶段，我们计算一个矩阵，其中包含代表成对比较结果的logit表示。给定此矩阵，我们可以推理出给定输入$x$的$N$个输出的排名。随后，我们可以将从PAIRRANKER中的每个输入的top-K个候选作为最终结果。因此，这种方法并不依赖于单个模型。相反，PAIRRANKER通过全面比较所有候选对，为每个示例选择最佳模型。
　　但是，这种方法可能会限制生成比现有候选更好输出的潜力。为了研究这种可能性，我们介绍了GENFUSER（第4节）模块，以融合N个排名候选的top-K输出，并为终端用户生成改进的输出。我们的目标是利用top-K候选的优势，同时减轻他们的弱点。
　　为了评估LLM ensemble方法的有效性，我们介绍了一个名为MixInstruct的基准数据集（2.2节）。在此数据集中，我们使用$N=11$个流行的开源LLM，来为由self-instruct形式化的各种指令遵循任务的输入生成$n$个候选输出。该数据集包括100K个训练示例和5K个验证示例，其中训练样例用于训练候选排名模块，例如我们的PAIRRANKER，以及5K测试示例，以用于自动评估。
　　在第5节中，我们对MixInstruct基准测试的经验结果表明，LLM-BLENDER框架可以通过结合LLM显着提高整体性能。PAIRRANKER做出的选择优于任何固定的单个LLM模型，如在基于参考度量和GPT-Rank中的出色性能所表明的那样。通过利用PAIRRANKER的top-K选择，GENFUSER通过有效融合输出以进一步增强响应质量。LLM-BLENDER在常规指标（即BERTScore，BARTScore，BLUERT）和基于ChatGPT的排名方面都取得了最高分数。LLM-BLENDER的平均排名在12种方法中为3.2，比最佳LLM的3.9高得多。此外，LLM-BLENDER的输出在top-3排名为总样例的68.59％，而Viccuna仅达到52.88％。我们认为，LLM-BLENDER和我们的发现将使从业者和研究人员通过ensemble学习部署和研究LLM。

2.Preliminaries

我们首先提供问题定义和两种常见的ensemble方法。接下来，我们介绍了为训练和评估目的而创建的数据集MixInstruct。最后，我们描述了我们的框架。

2.1 Problem Setup

给定一个输入$x$和$N$个模型 { M 1 , . . . , M N } \{\mathcal M_1,...,\mathcal M_N\} {M1​,...,MN​}，我们可以通过使用每个模型来处理$x$以生成$N$个候选输出。我们将候选输出表示为 Y = { y 1 , . . , y N } \mathbb Y=\{y_1,..,y_N\} Y={y1​,..,yN​}。在训练数据中，我们假设有一个真实输出$y$，器在测试评估期间则被隐藏。
　　在实际情况下，可能会选择一个固定模型，例如${\mathcal{M}}_9$，以推理所有未知示例（即，始终将$y_9$用作$x$的最终输出）。如果$M_9$在某些观察的示例中表现出明显更好的总体表现，这可能是合理的。但是，依靠预先选择的模型可能会导致次优性能，因为在各种情况下这$N$个模型可能具有不同的优势和劣势，这意味着，不同$x$输出的最佳选择可能并不总是来自同一模型。
　　我们的目标是开发一种ensemble学习方法，该方法为输入$x$产生输出$\hat{y}$，以最大化相似度$Q(\hat{y},y;x)$。$Q$函数可以通过各种方式实现，我们将在后面讨论。我们预计，对于$x$来说与使用固定模型或随机选择模型相比，此方法将产生更好的总体性能。具体来说，给定一个测试集$D_{test}=\{(x^{(i)},y^{(i)})\}$，我们的目标是最大化${\sum }_{i}Q({\hat{y}}^{(i)},y^{(i)};x^{(i)})$。
　　有两种结合LLM的主要方法：selection-based和generation-based的方法。基于选择的方法比较集合$\mathbb{Y}$中的候选输出，以选择最终的候选作为最终输出$\hat{y}$，这意味着$\hat{y}\in \mathbb{Y}$。由于选择的固有性质和有限的解决空间，基于选择方法的性能受被考虑的$N$个候选输出限制。相反，基于生成的方法着重于融合来自$\mathbb{Y}$的$K$个候选（$1<K\le N$），以产生未知响应作为最终输出$\hat{y}$。

2.2 MixInstruct: A New Benchmark

　　我们引入了一个新的数据集，MixInstruct，来作为在指令遵循任务中ensemble LLM的基准。如表1所示，我们收集了主要来自四个开源数据的一组指令样例。在设计和处理这批开源数据后，我们采样了100K个样例进行训练，5K进行验证和5K进行测试。然后，我们在这些110k个样例上运行$N=11$个流行的开源LLM，包括Vicuna，OpenAssistant，Alpaca，MPT等（见表2和图1）。
　　为了获得候选输出的排名，我们为ChatGPT设计了一个比较提示，以评估所有候选对。具体而言，对于每个样例，我们准备了55对候选（$11\times 10/2$）。对于每一对，我们要求ChatGPT判断更好的候选人（或宣布相同）。提示模板可以在附录中找到。对于训练和验证集，我们根据BERTScore，BLEURT和BARTScore等传统指标提供结果。在这种情况下，我们使用函数$Q(y_i,y)$来估计候选$y_i$的质量。

2.3 LLM-BLENDER: A Novel Framework

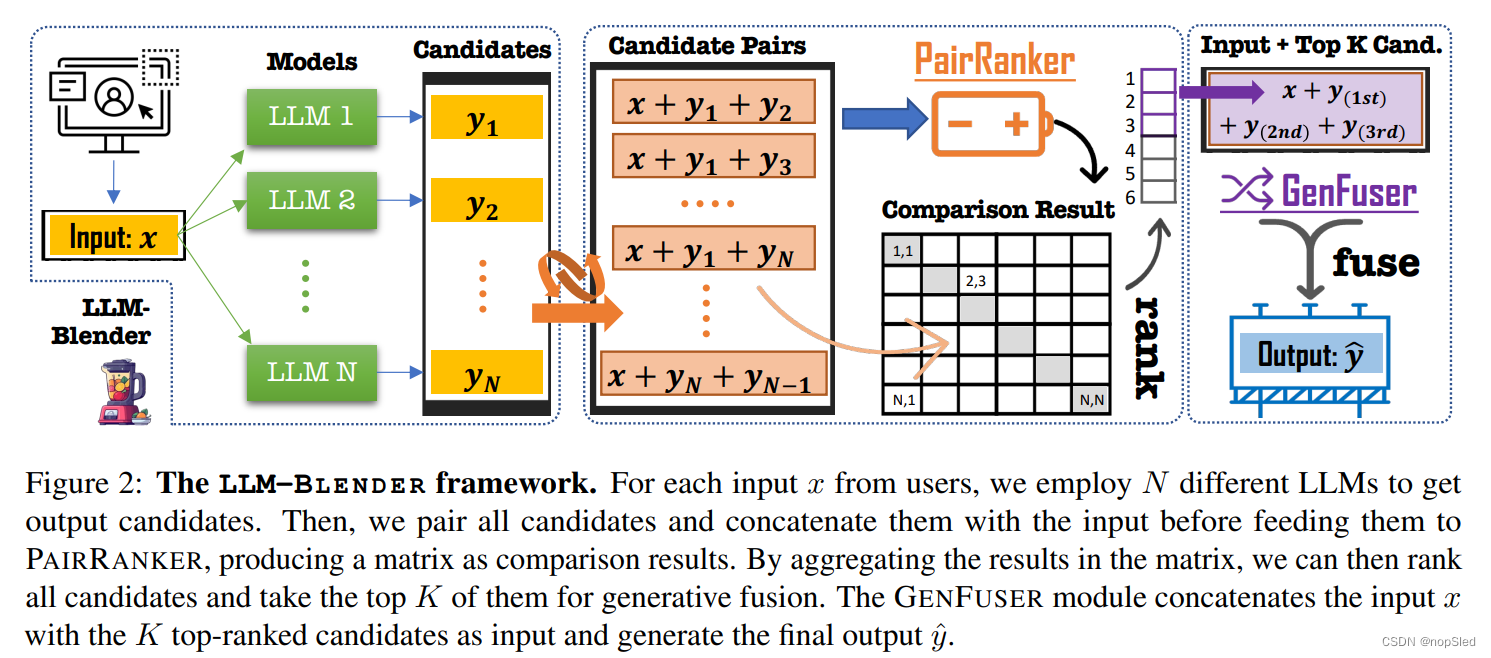
　　如图2所示，我们为ensemble LLM的排名提出了一个rank-and-fuse框架，LLM-BLENDER。 该框架主要由两部分组成：一个逐对排名模块PAIRRANKER（第3节），以及一个融合模块GENFUSER（第4节）。PAIRRANKER模块学会比较每个输入的所有候选输出，然后对候选列表进行排名。然后，我们选择$top-K=3$排名的候选，将其与输入$x$拼接，然后构造GENFUSER模块的输入序列。GENFUSER模块是一个seq2seq LM，最终生成了为用户服务的最终输出。

3.PAIRRANKER: Pairwise Ranking

在本节中，我们在3.1节介绍了三种基线方法，以对$\mathbb{Y}$中的候选进行排名。并随后提出了PAIRRANKER方法。

3.1 Baseline Methods

　　先前的重排序方法主要集中于计算每个候选输出$y_i\in \mathbb{Y}$的得分$s_i=f_{\varphi }(x,y_i)$，其中$s_i$仅由$y_i$确定。值得注意的是，GPT-3.5指令微调中的奖赏模型也属于此类。图3说明了这些基线方法，这些方法在以下段落中进一步详细介绍。
　　MLM-Scoring。MLM-Scoring通过计算其伪对数似然来评估候选输出的质量，这是通过逐一mask token，并使用屏蔽LM（例如BERT）来计算被mask token的对数似然获得的。给定一个候选$y_i$作为一个单词序列 W = { w 1 , . . . , w ∣ W ∣ } \textbf W=\{w_1,...,w_{|\textbf W|}\} W={w1​,...,w∣W∣​}，则伪对数似然是：$s_i={\sum }_{t=1}^{|\text{W}|}logP(w_t|{\text{W}}_{\setminus t})$。这种无监督的方法对于在NLG任务（例如机器翻译和语音识别）中的重排序输出是有效的。
　　SimCLS。SimCLS使用同一个编码器$H$分别编码输入$x$，以及每一个生成的候选$y_i\in \mathbb{Y}$，从而得到$H(x)$和$H(y_i)$。它们之间的余弦相似度被作为预测分数，即$s_i=cos(H(x),H(y_i))$，因为$H(x)$和$H(y_i)$共享由语言编码器得到的同一嵌入空间。在训练中，使用边缘排名损失优化$H$。
　　SummaReranker。SummaReranker使用交叉注意力编码器将输入$x$和每个候选$y_i$拼接以学习排名。具体而言，他们采用$H([x;y_i])$来预测得分$s_i$，其中$H$是Transformer模型。在训练阶段，采用二进制交叉熵（BCE）损失将最佳候选与其他候选者区分开来。
　　Limitations。尽管在训练中使用了对比损失，但这些方法仍依靠独立评分来推理。编码器尚未接触到直接用于比较学习的候选对。我们认为，在LLM和指令遵循任务的背景下，这些逐条排名方法可能不足以选择最佳候选。原因之一是，当选择的LLM是流行且竞争激烈时，LLM输出的质量通常很高。此外，与摘要任务不同，指令任务的响应可能是非常开放的。因此，仅检查单个候选可能不会产生可靠的分数。对于较短的响应而言，这个问题变得更加突出，其中两个候选序列可能只有几个单词差异，但在有用性，有害性和公平性方面有很大差异。鉴于这些局限性，我们认为独立评分方法可能无法捕获至关重要的细微差别。

3.2 Pairwise Comparisons

为了解决逐条排名的局限性，我们的目标是训练一个具有参数$\varphi$的排名器$f$，该排名器可以通过将其与输入文本一起编码来比较一个输出候选对。我们的排名模块应专注于学习捕获两个候选之间的差异，并倾向于质量更高的候选。
　　给定一对候选$y_i,y_j$，我们获得了他们的成对分数：$s_{(i,j)}^i$和$s_{(i,j)}^j$。我们将模型认为$y_i$比$y_j$更好的置信度表示为$s_{ij}=s_{(i,j)}^i{-}_{(i,j)}^j$。我们可以将这种分数用于所有从$\mathbb{Y}$中得到的候选对来推断最终排名。为了学习这种能力，我们将输入$x$和两个候选拼接以形成一个序列$[x;y_i;y_j]$并将其带入交叉注意力Transformer，以获取用于建模$s_{ij}$的特征：$f_{\varphi }([x;y_i;y_j])$。
　　我们假设有多个$Q$函数来优化，例如BERTScore，BARTScore等，并将学习问题视为多任务分类问题：
$${\mathcal{L}}_Q=-z_{i}log\sigma (s_{(i,j)}^i)-z_{j}log\sigma (s_{(i,j)}^j),$$
其中$\sigma$是sigmoid函数，并且，
$$(z_i,z_j)=\{\begin{array}{ll}(1,0),& Q(y_i,y)\ge Q(y_j,y)\\ (0,1)& Q(y_i,y)<Q(y_j,y)\end{array}.$$
当考虑到有多个$Q$，我们采用最终多目标损失的平均：$\mathcal{L}=\sum {\mathcal{L}}_Q$。

3.3 PAIRRANKER Architecture

　　我们在本小节中讨论了PAIRRANKER 模块的结构设计。
　　Encoding。我们采用Transformer层来编码输入和一对候选输出，从而使注意力能够在输入的上下文中捕获候选输出之间的差异。我们依次将这三个片段拼接，并用特殊字符作为分隔符来形成单个输入序列：<source>，<cantidate1>和<cantidate2>。最终的Transformers输入序列的形式是“<s><source>x</s><cantidate1>$y_i$</s><cantidate2>$y_j$</s>”，其中$x$是输入文本，$y_i$和$y_j$是两个候选文本。特殊字符<source>，<cantidate1>和<cantidate2>的嵌入分别用作$x$，$y_i$和$y_j$的表示，表示为$\text{x}$，${\text{y}}_i$，${\text{y}}_j$。
　　Training。为了确定两个候选的分数，我们分别将$x$的嵌入与$y_i$和$y_j$拼接，然后将它们通过单个分类层，这是一种多层感知器，最终层的维度等于要优化的$Q$函数的数量。此维度内的每个值代表特定$Q$函数的计算分数。我们通过平均这些$Q$分数计算候选的最终得分$s_{(i,j)}^i$或$s_{(i,j)}^j$。 由于存在$O(N^2)$个独特的配对组合，因此我们在训练阶段采用高效子采样策略来确保学习效率。
　　在训练过程中，我们从候选池${\mathbb{Y}}^2$中随机选择一些组合，而不是所有$N(N-1)/2$对。我们还通过将真实输出$y$混合到$\mathbb{Y}$中来扩展候选池，以将目标文本与其他候选进行比较。实际上，我们发现每个输入使用5对，就足以获得较好的结果。
　　由于语言模型的位置嵌入，因此候选输出的顺序$(x,y_i,y_j)$很重要。 因此，我们将每个训练对中的候选顺序打乱，以便该模型学会与自己保持一致。
　　Inference。在推理阶段，我们获得了每个候选对$(y_i,y_j)\in Y^2$的得分s_{ij}。在$N(N-1)$次迭代后，我们获得了一个矩阵$\text{M}$，其中${\text{M}}_i^j=s_{ij}$表示$y_i$比$y_j$更好的置信度。为了基于$\text{M}$确定最佳候选者，我们引入了三个聚合函数，以确定$\mathbb{Y}$的最终排名。
　　我们提出了两种评分方法，MaxLogits和MaxWins，它们利用矩阵中的所有元素。令${\text{M}}_i^{\ast }$和${\text{M}}_{\ast }^j$分别表示矩阵的第i行和第j列向量。对于每个候选$y_i$，其MaxLogits分数被定义为$s_i=\sum ({\text{M}}_i^{\ast }-{\text{M}}_{\ast }^i)$，而其MaxWins得分被定义为 s i = ∣ { s i j ∈ M i ∗ ∣ s i j > 0 } ∣ + ∣ { s j i ∈ M ∗ i ∣ s j i < 0 } ∣ s_i=|\{s_{ij}\in \textbf M^*_i|s_{ij}>0\}|+|\{s_{ji}\in\textbf M^i_*|s_{ji}<0\}| si​=∣{sij​∈Mi∗​∣sij​>0}∣+∣{sji​∈M∗i​∣sji​<0}∣，其中$||$表示集合的大小。
　　从本质上讲，MaxLogits计算了$y_i$优于所有其他候选的置信度，而MaxWins则计算与其他候选相比的胜利数量。
　　但是，这两种方法需要对$N$个候选进行$O(N^2)$次迭代，这可能是计算昂贵的。因此，我们提出了一种更有效的聚合方法，进行单个气泡排序，以成对比较来选择最佳候选。我们首先将$\mathbb{Y}$中的候选顺序打乱以获取一个默认顺序，并初始化最佳候选索引$k$为$1$。我们采用如下方式迭代地更新最佳候选索引：
$$k=\{\begin{array}{ll}k,& M_k^i-M_i^k>0\\ i,& M_i^k-M_k^i>0\end{array}.$$
　　在$N-1$比较之后，我们选择$y_k$作为最佳候选。该方法将推理时间复杂度从$O(N^2)$减少到$O(N)$，这与以前的逐条方法对齐。
　　无论采用聚合方法如何，我们都可以对$\mathbb{Y}$中的所有候选进行排名。我们的实验（附录中显示）表明MaxLogits会产生最优性能，因此我们使用MaxLogits作为PairRanker的默认PAIRRANKER。

4.GENFUSER: Generative Fusion

PAIRRANKER的有效性受到候选池$\mathbb{Y}$的选择质量的限制。我们假设通过合并多个top-k候选，可以克服这一约束。由于这些top-k候选经常展示互补的优势和劣势，因此可以通过减轻其缺点的同时结合优势来产生更好的反应。我们的目标是设计一个生成模型，该模型将输入$x$和top-k个候选 { y 1 , . . . , y k } ∈ Y \{y_1,...,y_k\}\in \mathbb Y {y1​,...,yk​}∈Y作为输入（例如，$k=3$），并产生改进的输出$\hat{y}$作为最终响应。
　　为此，我们提出了GENFUSER，这是一种以输入指令为条件，融合一组候选输出的seq2seq方法，以生成增强的输出。具体而言，我们使用分隔字符（例如<extra_id_i>）顺序拼接输入和$K$个候选，然后微调类似T5的模型以学习生成$y$。实际上，我们采用Flan-T5-XL，由于其出色的性能和相对较小的尺寸，该参数具有3B参数。

5.Evaluation